【データ分析でお困りのビジネスマン必見！】確率的な考え方や統計学の重要性を知ろう！（後編）

統計・機械学習トピック

公開日

2024年7月12日

更新日

2024年7月11日

みなさんこんにちは！和からの数学講師の岡本です。今回は前回に引き続き、「確率的な思考」の重要性について解説していきたいと思います。前編をご覧になりたい方はこちらをどうぞ。

【データ分析でお困りのビジネスマン必見！】確率的な考え方や統計学の重要性を知ろう！（前編）

この「確率」という概念を用いた統計的手法は「推測統計」と呼ばれ、あらゆる分析を行う際の基本的な考え方に直結します。それでは、前編で提示した問題の復習から入ってみましょう。

この記事の主な内容

１．確率的な感覚について（再掲）

前編では、以下のような確率に関するちょっとしたテストを行ってみました。

第1問：勝率１％のミニゲームを100回行った場合、少なくとも1回勝利する確率として最も近いものを次の①～⑤の中から選んでください。

　　①1%未満　　②20%程度　　③40％程度　　④60％程度　　⑤80％以上

第2問：コインを1000回投げて、550回以上表がでる確率は？

　　①1%未満　　②20%程度　　③40％程度　　④60％程度　　⑤80％以上

どれが正解なのかわかりましたか？

２．確率の問題の正解は…？

上記の問題の正解を発表します。まず、第1問の正解は、④の「60％程度」です！正確には約63.4％となります。スマホアプリなんかの「ガチャガチャ」をイメージしてみましょう。当たりを引く確率が１％であるガチャを100回やっても、必ず当たりを引けるとは限らないのです！実際に少なくとも1回当たりを引く確率は約60％となり、意外にも低いですね…。なお、確率の計算ができるようになると、90％以上にするには何回以上ガチャを引けばいいかを逆算することもできます！

次に、第2問についてですが、正解は…　①の「１％未満」です。ちなみに実際はなんと0.09％以下となります！「え！？そんなに小さいの！？」と思われる方が多いのではないでしょうか？このように、直感とは異なる現象はあらゆるところで起こり得ます。しっかりと数字をもとに予測や確率的な戦略ができていないと、ビジネスの世界では恐ろしいことになる可能性があります。例えば、新商品の開発を行う際、需要の予測を行います（これを怠ると、需要がないのに膨大な予算を掛けて商品開発に踏み切ってしまうことになり、大きな損失につながります）。需要予測も確率の理論をもとに計算されるものです。この部分の計算が正しくつかめていないと、効果的な施策や売上増加につながりません。

３．確率計算の解説（第１問）

第1問の計算についてですが、まず重要なのが「余事象」の考え方です。

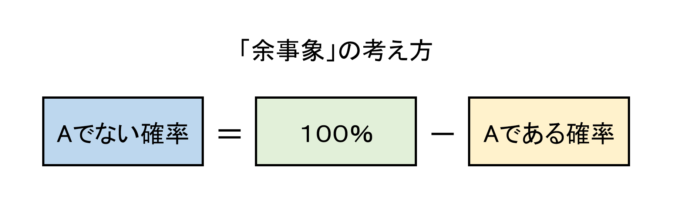
「100回中少なくとも１回当たりが出る場合」というのは、「100回中全て外れる場合以外」と考えることができます。したがって、求める確率は100％から「100回中全て外れる確率」を引けばいいわけです！外れる確率は99％で、これが100回起こるという確率は、
\begin{align*}
0.99\times 0.99 \times 0.99 \times \cdots \times 0.99 =(0.99)^{100}=0.366032…
\end{align*}
と計算できます（これは「反復試行」の考え方です）。したがって、「100回中少なくとも1回当たる確率」は
\begin{align*}
1-0.366032=0.633968
\end{align*}
となり、約63.4%であることが計算できました。
なお、この計算はExcelを用いると[=1-(0.99)^100]で計算できます。

４．確率計算の解説（第２問）

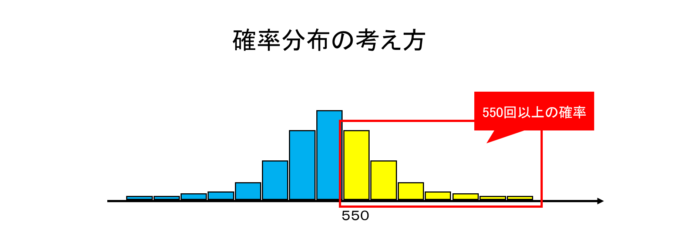
続いて第2問の解説に入ります。「1000回中550回以上表がでる確率」とは、「1000回中550回表が出る確率」＋「1000回中551回表が出る確率」＋…＋「1000回中1000回表が出る確率」という具合に550回から1000回の場合まで確率を合計することによって得られます。また、「\(n\)回中\(k\)回表がでる」というのは「組み合わせの数」と言われていて、コンビネーションの公式\({}_nC_k \)を用いて計算できます（高校1年生で登場します）。これを使って1000回中\(k\)回表がでる確率は
\begin{align*}
{}_{1000}C_k\cdot (0.5)^k(0.5)^{1000-k}={}_{1000}C_k\cdot (0.5)^{1000}
\end{align*}
となり、\(k\)を550から1000まで合計すれば0.000865という結果が得られます。ここで使った計算は「二項分布(Binomial distribution)」と呼ばれる確率分布の公式で、現在では高校2年生で学習します。この他にも誤差の分布として使われる「正規分布(Normal distribution)」や待ち時間の分布「指数分布(Exponential distribution)」、一定時間内のイベント発生回数の分布である「ポアソン分布(Poisson distribution)」など、様々な確率分布モデルがあり、マーケティングや金融工学の世界で活用されています。

なお、上記の計算はExcelでは[=1-BINOM.DIST(549, 1000, 0.5, TRUE)]で計算できます。
「BINOM.DIST(Ａ, Ｂ, p, TRUE)」で「成功確率pの試行をB回行ってＡ回以下成功する確率」を出力します。そのため、今回は1000回中549回以下の確率を１から引くことで求めています。

５．さいごに

　ここまでお話にあったように、皆さんの思った以上に確率の考えは世の中で活用されています。確率の知識や感覚は「あったほうが得」ではなく、むしろ「ないと損」という時代になってきました。こうしたこともあって統計やデータ分析に関する学習を始められる方はここ数年で激増しています。私自身、講師としてお客様から現状や学習相談をこれまで何度も対応させていただきました。その際多くのお客様から、「いろんな参考書やネットで学習を進めてきたけれども、どうしても身につかない」、「そもそもどこから初めて、どこに向かっていけばいいのかわからない」といった状況をお聞きします。確かに、データ分析や確率、算数や数学も合わせると正直とても範囲が膨大です。ネットや書店に行けば、いい解説ページや本がたくさん手に入るのは事実なのですが、どうしても断片的で、つながりや理解しにくいように感じます。
　学習において重要なのは「つながり」です。いま学習していることがどこで活かされるのか、どんな応用があるのか、こうした不安を解消していただくために、弊社ではロードマップをはっきりと示し、一通りの流れを正しく学習する統計学のオンラインセミナーを実施しています。どこから初めていいかわからず迷われている皆様、迷っている時間や、非効率な学習に費やす時間とお金は、場合によっては損をしている可能性があります！そんなときは、ぜひとも無料のオンラインセミナーへいらしてください。今後の指針や取り組みは間違いなく変わってくると思います！

統計学を初めて学習される方向けの無料講座
統計超入門セミナー