数学の授業で学んだ「集合」を覚えていますか？通常は高校1年で学ぶものですが、文系に進んだ人は、何のために学んだのだろう？と思われるかもしれません。

集合の考え方は、物事を論理的に考える上で基本となる概念です。Wikipediaの「論理学」の項では、その概要が以下のように記述されています。

“ここでいう論理とは、思考の形式及び法則である。これに加えて、思考のつながり、推理の仕方や論証のつながりを指す。よく言われる「論理的に話す、書く」という言葉は、つながりを明確にし、論証を過不足なく行うということである。”

つながりという言葉が使われていますが、論理的思考力は、「2つの事柄のつながり（関係性）を正しく認識する能力」ということが言えます。この場合の「事柄」を定義するために、集合の考え方が必要なのです。

ちょっと復習の意味で、全体集合を「1～20の整数」とし、部分集合Aを「2の倍数」、部分集合Bを「5の倍数」とした場合のことを考えてみましょう。ベン図で下記の図のように表されます。

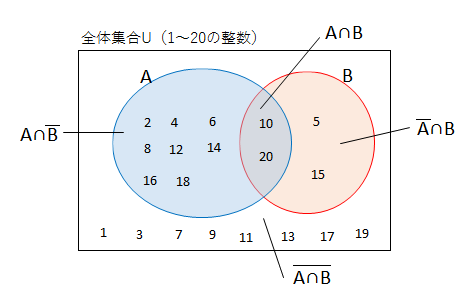
全体集合が4つのグループによって「漏れなく、ダブりなく」構成されていて、且つそれぞれのグループ同士のつながり（関係性）が明確になっていることが分かるかと思います。

「MECE」って何？

皆さんは、会社で上司や先輩から「MECE（ミーシー）」という言葉を聞いたことがあるかもしれません。「MECEに考えよう」とか「その分類はMECEじゃないね」とか、そんな風に使われます。初めて聞くと「何それ？」と思うことでしょう。

MECEとは、Mutually Exclusive and Collectively Exhaustiveの頭文字を取ったもので、単語を一つ一つ訳すと以下のようになります。

Mutually＝互いに
Exclusive＝排他的な
Collectively＝全体で
Exhaustive＝網羅的な

簡単に言うと、MECEとは「漏れなく、ダブりなく」という意味で、特に何かを分類する際に注意すべき基本的な考え方です。

「MECE」に分類するってどういうこと？

例えば、「新商品を開発して日本国内で販売する。どんな人をターゲットにマーケティング資源を投下すべきか」

こういう命題があった場合、顧客となる可能性のあるグループの全体（全体集合）を、例えば日本在住者とします。全体集合は、いろいろな「切り口」で分類できるでしょう。「切り口」の例としては、「性別」「年齢層」「未婚／既婚」「居住地」「働いている／働いていない」「年収」「子供がいる／いない」「国籍」などさまざまなものが考えられます。これを、MECEに、且つ分析に有効な分類をするにはどうすればよいでしょうか。

MECEに対象を分類するのに、最もシンプルで汎用的によく使われるものとしては、2軸4象限のマトリックスがあります。皆さんもこんな図を見たことがあるのではないでしょうか？

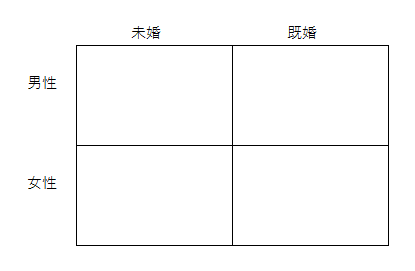
「性別」「未婚／既婚」という、それぞれ絶対に重複しない対立項(※注)による「軸」を2つクロスさせて、4つの象限をつくります。これによって、ある対象のグループをMECEに分類することができます。

では、こんな図を見てどう思いますか？

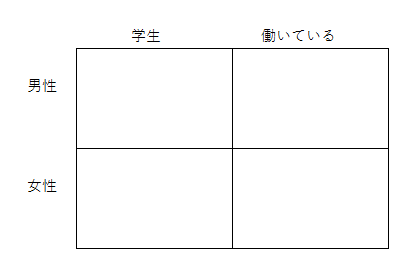
「性別」は重複しない対立項ですが、「学生／働いている」はどうでしょうか。学生でアルバイトをしている人、会社に勤めながら大学に通っている人もいるかもしれません。その場合、重複になってしまいます。また、専業主婦の方や、定年を迎えて、学生でもなく働いてもいない人もいるでしょう。つまり、漏れがあります。これではMECEとは言えません。

なぜ「MECE」に考える必要があるの？

先輩や上司に「それはMECEじゃないな」なんて言われたりしたら、それは対象を分類する際の「切り口」の設定の仕方が間違っていて、きれいに分類できていない、ということです。

でも、なぜMECEに考える必要があるのでしょうか？

例えば、「キャンプに行くときに準備するものリスト」をつくる場合を考えてみましょう。

テント、BBQ用のコンロ、飯ごう、寝袋、懐中電灯、帽子…と何のアテもなくバラバラに挙げていっても、何か忘れ物がないか不安ですよね。そうならないように、例えば以下のように、キャンプの行程を場面ごとに分けて考えてみると、考慮漏れをなくすことができます。

・移動時
・テント設営時
・料理・食事の時
・寝る時
・遊ぶとき

このように、物事を考える際に、思考のガイドになる枠組みを用いることを「フレームワーク」と言います。誰しも学校で習った「5W1H」なんかもフレームワークの1つですし、ビジネスで用いられるものとしては「3C分析」「SWOT分析」などが有名ですが、これらのフレームワークを使いこなすために必要な、基本的な考え方がMECEなのです。

でも、ただMECEなら良い、というわけではありません。上の「新商品を開発して日本国内で販売する。どんな人をターゲットにマーケティング資源を投下すべきか」の例で、その新商品が口紅だったとしたら、「性別」を軸に持ってきても意味がないでしょう。そもそもの母集団の設定が間違っています。その場合は、全体集合を日本在住者ではなく、「○歳～○歳の女性」などとするべきです。対象とする全体集合をどこまで広げるか、もしくはどこまで絞るかは、集合を扱う場合に重要な点です。

うまく対立項を見つけられない場合は？

軸には絶対に重複しない対立項を用いましょう、と言いました。対象が人であれば「性別」などが「絶対に重複しない対立項」でしょうし、何かの商品の営業対象を考えるなら「法人／個人」、学校なら「公立／私立」といったような対立項が考えられます。ただ、必ずしもこのような分かりやすい「対立項」を見いだせるとは限りません。この辺りが難しくて、2軸４象限のマトリックスをうまく使えない人もいます。

その場合は、数学の「集合」で考えてみましょう。ある集合とその補集合で一つの軸をつくるという考え方もあるのです。

集合を図式化する「ベン図」は、見覚えがある人も多いのではないでしょうか。上記の例に挙げた口紅などの化粧品のマーケティング対象を考えるのであれば、商品の特性から「仕事の時に使うのか、プライベートで使うのか」によってプロモーションのコンセプトが変わりますし、購入シーンによって販売戦略も変わってきたりするはずです。

無理に明確な対立項を見いださなくても、明らかにしたいことに応じて、例えば使う場面を分類したい場合は「ビジネスシーンで使うことが多い『会社勤め』の女性」とか、購入場所を想定して「デパートで買う人」といったように、具体的なターゲットのグループを一旦定義し、その補集合を対立項にする手法を採ってもよいのです。

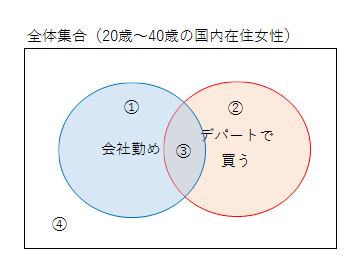
上記のようなベン図を、2軸4象限の図に描き直すとこうなります。

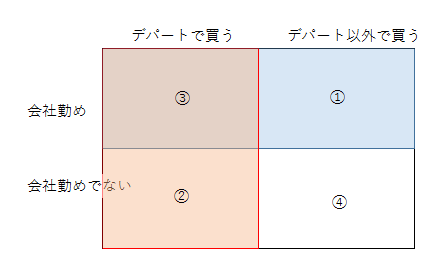
このように考えれば、うまく「対立項」が見つけられない場合でも、有用なターゲット設定、マーケティング施策のアイデアにつなげられるのではないでしょうか。

「2軸じゃ足りないのですが…」

ビジネスの場では、2軸4象限の図をよく見かけます。ただ「2軸だと足りなくて、もう1つ軸を設けて分類したいんだけどな…」という場合があるかもしれません。3軸での分類を上手く視覚化しようと思ったら、その時は、「キャロル表」（「キャロル図」と呼ばれる場合も）を用いてみましょう。

キャロル表とは、下の図のようなものです。先ほどの2軸４象限の図の真ん中に、各象限にかかるような長方形を書きます。この長方形の内側と外側で、一つの「軸」を表現するのです。対立項を軸にしてその3つの軸をクロスさせることにより、2の3乗で8つのMECEなグループ分けを、分かりやすく視覚化できます。

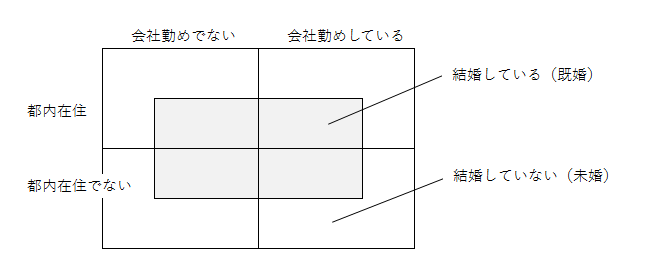
このキャロル表の名前は、ルイス・キャロルの名前から来ています。ルイス・キャロルとは、かの有名な『不思議の国のアリス』の作者です。数学に造詣が深い方ならご存知の方も多いかもしれませんが、彼は数学者・論理学者でもありました。

元々は、ルイス・キャロルが子ども向けの論理ゲームの一つとして考案した図なのですが、3軸の分類が一目で分かる図として優れています。ビジネスの場面で2軸4象限のマトリクスを見慣れている人は多いですが、キャロル図をさりげなく使ってみると、一目置かれるかもしれません。ぜひ試してみてください。

※注（追記）
MECEをシンプルに説明するために「性別」を生物学的な性別として捉え、「絶対に重複しない対立項」と説明しました。ただ、性別と言った場合、ジェンダー（社会的な性別）の考え方もあります。その意味では、「絶対に重複しない」とは言えませんし、厳密にMECEに分けようとすると、もっと複雑な分類になるでしょう。

ビジネスでMECEを意識する場合に重要なのは、必ずしも厳密にMECEに分類することではありません。分類する「目的」に応じて適切な「軸」を設定しましょう。

（文／畑邊康浩）