忘れた頃に登場する“相加相乗平均の不等式”
公開日
2025年7月23日
更新日
2025年7月29日
こんにちは!和からの数学講師の岡本です。
今回は、入試問題や大学数学において様々な分野で忘れた頃に登場する「相加相乗平均の不等式」について考えていきます。
この記事の主な内容
1.相加平均と相乗平均
まず、相加平均と相乗平均の定義から始めましょう。正の実数 \(a_1,a_2,\ldots, a_n\) において、相加平均とは
\begin{align*}
\frac{a_1+a_2+\cdots+a_n}{n}
\end{align*}
で定義される値です。私たちが普段「平均」と言えばこの式が思い浮かぶと思います。足し算的な平均ということから「相加平均」と呼ばれていますが、算術平均(Arithmetic Mean)とも言われます。また、相乗平均とは
\begin{align*}
(a_1\times a_2 \times \cdots \times a_n)^{\frac{1}{n}}
\end{align*}
で表される値で、\(n\) 個を掛け合わせたものの \(n\) 乗根をとる計算になっています。これは掛け算的な平均ということから「相乗平均」と呼ばれていますが、幾何平均(Geometric Mean)とも呼ばれています。
2.相加・相乗平均の不等式
面白いことに、相加平均と相乗平均には次のような明確な大小関係があることが知られています。
\begin{align*}
\frac{a_1+a_2+\cdots+a_n}{n} \geq (a_1a_2\cdots a_n)^{\frac{1}{n}}.
\end{align*}
つまり、同じ正の実数 \(a_1,a_2, \ldots, a_n\) に対して、常に相加平均の方が相乗平均よりも大きいことが知られています。なお、等号が成り立つのは \(a_1=a_2=\cdots=a_n\) のときのみとなります。このような不等式を「相加相乗平均の不等式」と呼びます(AM-GMの不等式と略記することもあります)。この不等式は解析学や統計学など、あらゆる数学の分野や入試問題などでよく目にします。ただ、「よく目にする」と言っても、数列や微積分のように、当たり前のように登場するほどでもなく、大小関係の評価の中でひっそりと顔を出す程度です。そのため受験生の間では「そうか、そうかの相加・相乗平均」と言われていたりします。しかし、相加・相乗平均の不等式を使うことで解法が極端に簡潔になることが多く、できればうまく使いこなしてもらいたい不等式です。
3.不等式が成り立っていることの確認
\(n=2\) の場合について確認してみましょう。例えば \(a_1=1,a_2=4\) の場合、相加平均は \((1+4)/2=2.5\)。相乗平均は \(\sqrt{1\cdot 4}=2\) となり、確かに相加平均の方が大きくなっています。このように、相加・相乗平均の不等式において不等式の向きを忘れた場合は \(a_1=1,a_2=4\) について考えると楽に確認できます。また、\(n=2\) の場合の不等式の証明を行ってみましょう。示したい不等式の両辺を 2 倍し、2 乗した \((a_1+a_2)^2 \geq 4a_1a_2\) が成り立つことを示せばよいので、左辺から右辺を引いた式を考えましょう。
\begin{align*}
(a_1+a_2)^2 – 4a_1a_2 &= a_1^2 + 2a_1a_2 + a_2^2 – 4a_1a_2 \\
&= a_1^2 – 2a_1a_2 + a_2^2 \\
&= (a_1 – a_2)^2 \geq 0
\end{align*}
となり、これにより示したい式を得ることができました。
4.図を用いた \(n=2\) の場合の証明
続いて、図を用いた \(n=2\) の場合の証明をご紹介しましょう。次の図のように、直線上に点 \(A,B,C\) をとり、\(AB=a, BC=b\)(ここでは \(a < b\) としておきましょう)とします。また、\(AC=a+b\) を直径にもつ円を考え、円の中心点を \(O\) としておきます。
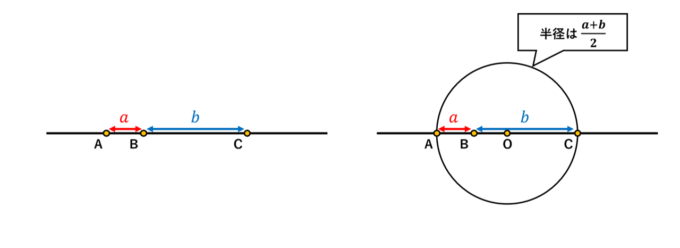
このとき、\(B\) を通る、\(AC\) に垂直な線を引き、円との交点をそれぞれ \(D,E\) とします。
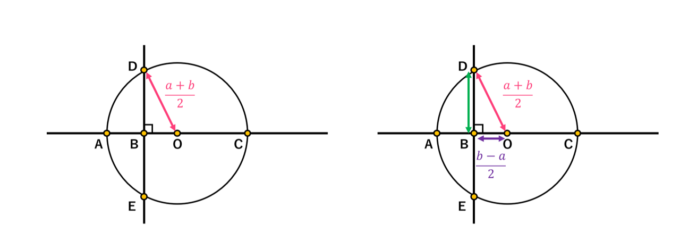
円の半径は \(\frac{a+b}{2}\) であることから、\(BD\) の長さは三平方の定理より
\begin{align*}
BD &= \sqrt{OD^2 + BO^2} \\
&= \sqrt{\left(\frac{a+b}{2}\right)^2 – \left(\frac{b-a}{2}\right)^2} \\
&= \sqrt{\frac{a^2 + 2ab + b^2}{4} – \frac{b^2 – 2ab + a^2}{4}} \\
&= \sqrt{ab}
\end{align*}
となります。図から明らかなように \(BD\) は半径より小さいので、相加相乗平均の不等式 \( \sqrt{ab} < \frac{a+b}{2} \) が成り立つことがわかります。
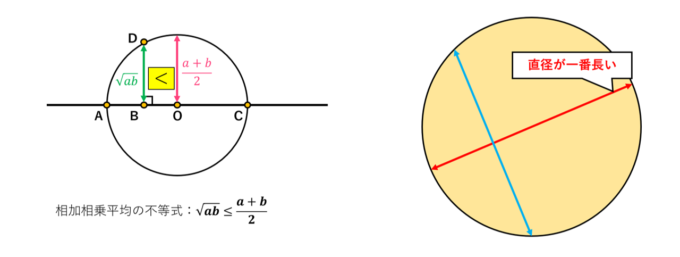
なお、等号成立条件は図から \(a=b\) の場合であることがわかります。つまり、\(n=2\) の場合の相加相乗平均の不等式というのは、「円周上の 2 点を結ぶ線分の長さの最大は直径である」という非常に直感的なことを言い換えているにすぎないことがわかりました!
5.さいごに
いかがでしたでしょうか?「相加相乗平均の不等式」は、一見すると地味な存在かもしれませんが、証明の簡潔さや応用の幅広さなど、非常に奥深い魅力を秘めています。
次回は、この不等式の一般の \(n\) に対する証明や、他にも知られている美しい証明方法をご紹介していこうと思います。どうぞお楽しみに!
和からのセミナーで、数学をもっと深く楽しもう!
和からでは、今回のような数学の面白さ・不思議さを体系的に学べる「高校数学の学び直しセミナー」を開催中です。高校3年間の数学を48回でやり直すコースや、数学の背景にある理論や歴史に迫る講座まで、幅広くご用意しています。
▼高校数学学び直しセミナーはこちら▼
▼大人が数学を楽しみながら再学習するために…無料セミナーのお申し込みはこちら▼
▶ 和からのセミナー一覧:こちら
▶ お問い合わせフォーム:こちら
▶ 数学とアートが融合した岡本の著書です:
アートで魅せる数学の世界 岡本健太郎(著) 技術評論社
<文 / 岡本健太郎>