やさしく学ぶ統計学~重複組み合わせとは?~
公開日
2023年4月16日
更新日
2023年4月16日

みなさんこんにちは。和からの数学講師の伊藤です。以前紹介した組み合わせの考え方に続いて、今回は重複組み合わせの考え方を見ていきたいと思います。重複組み合わせの問題を解く際に有効な方法についても触れていきますので、その点にもご注目ください!
↓以前の組み合わせの記事
この記事の主な内容
1. 重複組み合わせとは?
今回は、次のような問題を考えましょう。
➁青色の玉3個と赤色の玉3個の中から3個の玉を選ぶとき、玉の選び方は何通り?
※➁の問題については、玉の数を「3個」と限定する必要はなく、たくさんある(同一の)赤と青の玉の中から3個取り出す際の組み合わせを計算することになります。
前回の記事で紹介した通り、これらの問題を考える際には注意したい違いがあります。➀の問題はすべての玉が異なっているため、組み合わせ記号\(C\)を使って\({}_6C_3=20\)通りと計算することができます。一方➁の問題は、同じ色の玉に区別がない状況です。つまり、➀の問題における次のような状況は全て同じと見なします。
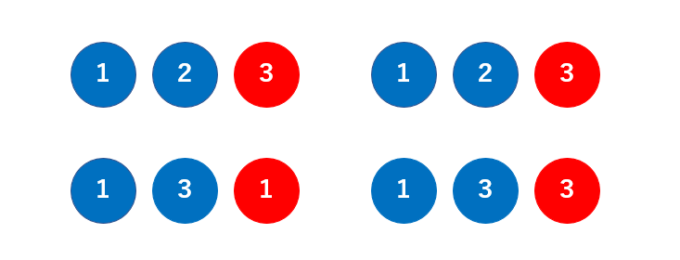
このように、重複する物の中から組み合わせを考える状況を重複組み合わせと呼びます。この後は重複組み合わせを考える際の記号と公式を紹介し、さらに重複組み合わせの考え方にも触れていきます!
2. 組み合わせの表し方と計算方法
重複組み合わせは、\(n\)種類の(同一の)物から、重複を許して\(m\)個を選ぶ組み合わせを表します。なお、\(n\)と\(m\)の大小関係には特に制限はありません。また選んだ\(m\)個すべてが同じものでも構いませんし、全て異なっていても問題ありません。このような重複組み合わせは、記号\(H\)を用いて以下のような計算をして場合の数を求めます。
\begin{align*}
{}_nH_m={}_{n+m-1}C_m
\end{align*}
左辺が、\(n\)種類の(同一の)物から重複を許して\(m\)個を選ぶ場合の数を表す記号、右辺がその場合の数の求め方ということになります。組み合わせ記号「\(C\)」のみで計算できるので、覚えてしまいさえすれば問題なく解くことができます。
今回の問題➁は2種類の玉から重複を許して3個を選ぶ場合の数を求めればよいので、\({}_{2+3-1}C_3={}_4C_3=4\)通りとなります。
3. 重複組み合わせの考え方
最後にご紹介するのは、今回紹介した重複組み合わせの考え方です。\(n\)種類の(同一の)物から\(m\)個の物を選ぶ場合、「\(m\)個の〇と\(n-1\)個の仕切り」を想像すると簡単に解くことができます。

とくに今回の問題に合わせて、2種類の玉から3個取り出すという場合の数を、3個の〇と1個のしきりで考えましょう。
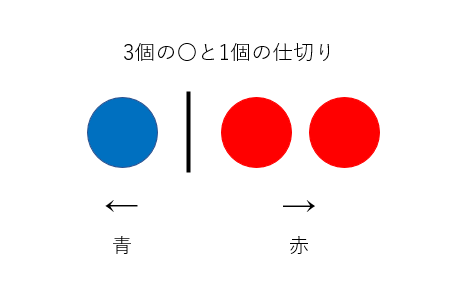
たとえば上記のように〇と仕切りが配置されている場合、左から数えてはじめの仕切りまでの〇を青とし、その右にある〇を赤とすれば、重複を許して3個の玉を選んだ状況を作ることができます。同じように考えると、\(m\)個の〇と\(n-1\)個の仕切りという重複した物を1列に並べることで、何を何種類選んだかを決定することができます。
よって、重複組み合わせは、対象を区別しない順列の考え方を使って以下のようにも計算することができます。
\begin{align*}
\frac{(n+m-1)!}{m!(n-1)!}
\end{align*}
実際に式を変形してみると、先ほど紹介した\(H\)を使用した式と同一の計算になっていることが分かります!実際、問題➁をこの方法で解いてみると、\((3+2-1)!/\{3!(2-1)!\}=4!/3!=4\)通りとなります。
〇と仕切りの考え方が分かると、難しい場合の数を計算する際に役立つことがあるかと思います。計算だけではなく、どのような仕組みになっているのかもぜひ覚えておいていただければと思います!
●和からのセミナー案内
Excelを用いたデータ分析のストーリーや可視化のスキルを学んでいくセミナーのご紹介です。興味を持っていただけた方は、ぜひ覗いてみてください!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/伊藤智也>












