↓↓↓動画で見たい方はこちら↓↓↓

みなさんこんにちは。和からの数学講師の伊藤です。先日、古代ギリシャの時代に活躍していた数学者のピタゴラスに関する記事を書きました。

「三平方の定理」で見つかった矛盾！？ピタゴラスの生涯

その際に軽くご紹介しましたが、ピタゴラスが発見した音楽と数学の関係性がなかなか面白かったので、今回はその記事を書いてみようと思います！

１．ピタゴラスの発見

ピタゴラスと言えば三平方の定理が有名ですが、彼の発見はこの定理だけではありません。日常生活の中のふとした気づきによって、現代でも使われる音楽と数学との関係性を発見したのです。

ある日ピタゴラスが鍛冶屋の前を通りかかったとき、職人が打つ鉄の音が、きれいにハモっているときとそうでないときがあることに気付きました。そこで詳しく調べてみたところ、職人が使うハンマーの重さによって音が変わっており、ハンマーの重さが一定の整数比になっているときに、美しい音が響いていることが分かったそうです。

その後、ピタゴラスとその弟子がモノコードという簡易的な楽器を作り、同時に鳴らしたときにきれいに響く音程を調べました。そこで発見したのが、弦の長さが2:1、3:2、4:3の時に、音が綺麗にハモっているということでした。実は現在使われているドレミファソラシドの音階にも、この性質が当てはまっているというのです！詳しく考えてみましょう。

２．用語の確認

高さが違う2つの音が同時になっている音を和音と言いますが、それらの音がきれいに響いているとき、特にこれらの音を協和音と呼びます。逆に、協和していない和音のことを不協和音と呼びます。

それから、2つの音の高さの差を音程と言いますが、この音程は、度数という言葉で表現されます。全く同じ音を1度と呼び、ドレミファソラシドの音階が1つ、2つとずれていくときは、2度、3度と数えていきます。

ということは、2つの音が鳴ったときの音程には、協和音程と不協和音程があることになります。これらの音程の中でも、最も濁りがなくきれいに協和している音程を、完全〇度の協和音と言います。この後お話をしますが、ピタゴラスは、この完全協和音程を発見していったということなのです。

３．ピタゴラスの発見から音階を作ってみる

1章でお話したピタゴラスの発見から、周波数が2:1、3:2、4:3の整数比を持つ場合に美しい音が響くことが分かりました。では、実際にこれらの比の関係性を持つ数は何があるでしょうか。具体的に挙げてみると、12・8・6や12・9・6といった組み合わせが考えられます。

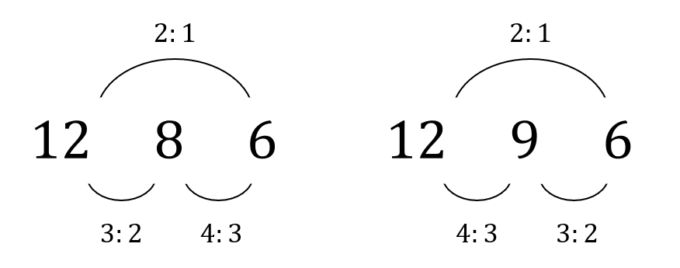
これらは要するに、どの二つをとっても美しい音が響く周波数（の比）の組み合わせということになります。これをもとにして、6・8・9・12に、ドレミファソラシドの中の「ド」、「ファ」、「ソ」、「ド」を対応させます。

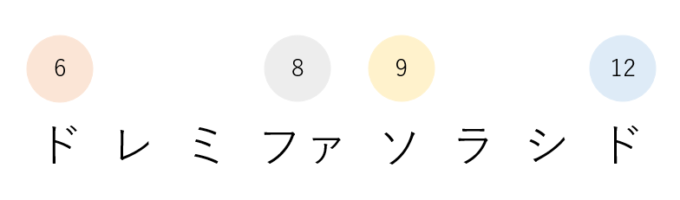
つまり、基準となる「ド」の完全8度の協和音が1オクターブ上の「ド」で、完全5度の協和音が「ソ」、完全4度の協和音が「ファ」になります。他の音も、この関係をもとに考えることができます。「レ」は「ソ」と完全4度の音、「ラ」は「レ」と完全5度の音、「ミ」は「ラ」と完全4度の音、「シ」は「ミ」の完全5度の音となっています。これらの音階を先ほどの規則から求めてみると、それぞれの音階には次のように数字が対応することが分かります。

例では、「レ」の音が「ソ」の音と完全4度の関係にあることから、音程の比が3:2になるという式を考えています。この続きは、ぜひ皆さんも考えてみてください！音程の中にも数学が使われていたと知ったときは、個人的になかなか驚きでした…！

４. まとめ

いかがでしたでしょうか。ピタゴラスが発見した音程に関するお話でした。先日の記事でもお話した通り、ピタゴラスは、「世界は整数の比でできている」という考えを信じていました。まさかそれが音楽の世界でも成り立ってしまっていたとは…この考えに陶酔してしまっていたと言われているのも不思議ではありませんね。

それでは、また次回のマスログでお会いしましょう！

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/伊藤智也>

アーテック(artec)【科学工作】音の正体 手作りモノコード