点対称と線対称【算数からやさしく解説】
公開日
2022年8月28日
更新日
2025年9月18日
↓↓↓動画で見たい方はこちら↓↓↓
https://youtu.be/Mo6YlLbhlNg/p>
この記事の主な内容
点対称と線対称
「図形が対称である」というとき、一般的には点対称と線対称の\(2\)種類のパターンが考えられます。
点対称であるとき、図形は「対称の中心」に対して\(180\)°回転しても元の図形に戻ります。
線対称であるとき、図形は「対称軸」に対して\(2\)つにピッタリ重なる形で折り合わせることができます。
点対称と線対称は似て非なる概念なので、その違いを知って使い分けることが必要です。また、関連する「対称の中心」や「対称軸」といった独特な用語の意味を学びましょう。
点対称
対称の中心について\(180\)°回転したとき、元の図形に重なる図形のことを点対称な図形と呼びます。図形が点対称であるとき、対称の中心は重心の位置と一致します。
早速具体例を考えてみましょう。

上の図形は点対称な図形になります。図形を\(180\)°回転すると、Aの点がA’の位置に移動します。反対に、A’の点はAの位置に移動します。このような二つの点A、A’を対応する点と呼びます。
AとA’の関係について詳しく見てみると、OA=OA’(AからOの長さ=A’からOの長さ)であることが分かります。また、A,O,A’は一直線上にあるので∠AOA’(頂点Oの角度)は\(180\)°になります。
上の図を見ると、対応する点同士を結んだ線が全て\(1\)点(対称の中心)で交わることが分かります。
また、OA=OA’であったように、図形上の点(A)から中心(O)の距離は対応する点(A’)から中心(O)の距離と等しいです。
点対称な図形には\(180\)°回転させると等しくなることに加えてこのような性質があります。
線対称
対称軸について図形を折り返したとき、対称軸の両側が完璧に重なる図形のことを線対称な図形と呼びます。図形が線対称であるとき、重心は対称軸上に位置します。また、対称軸が複数ある時、重心は対称軸の交点です。
例を用いて具体的に考えてみましょう。
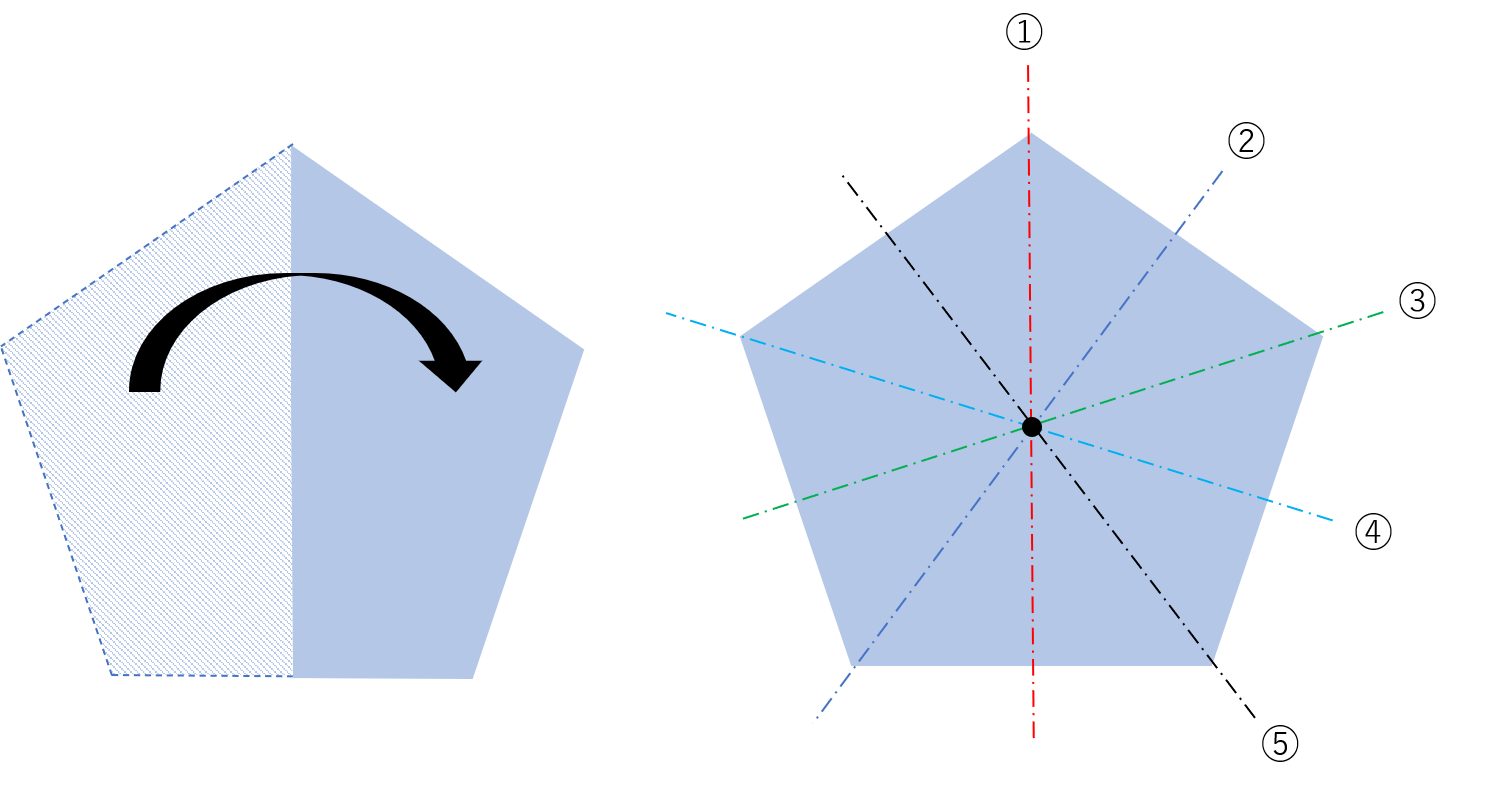
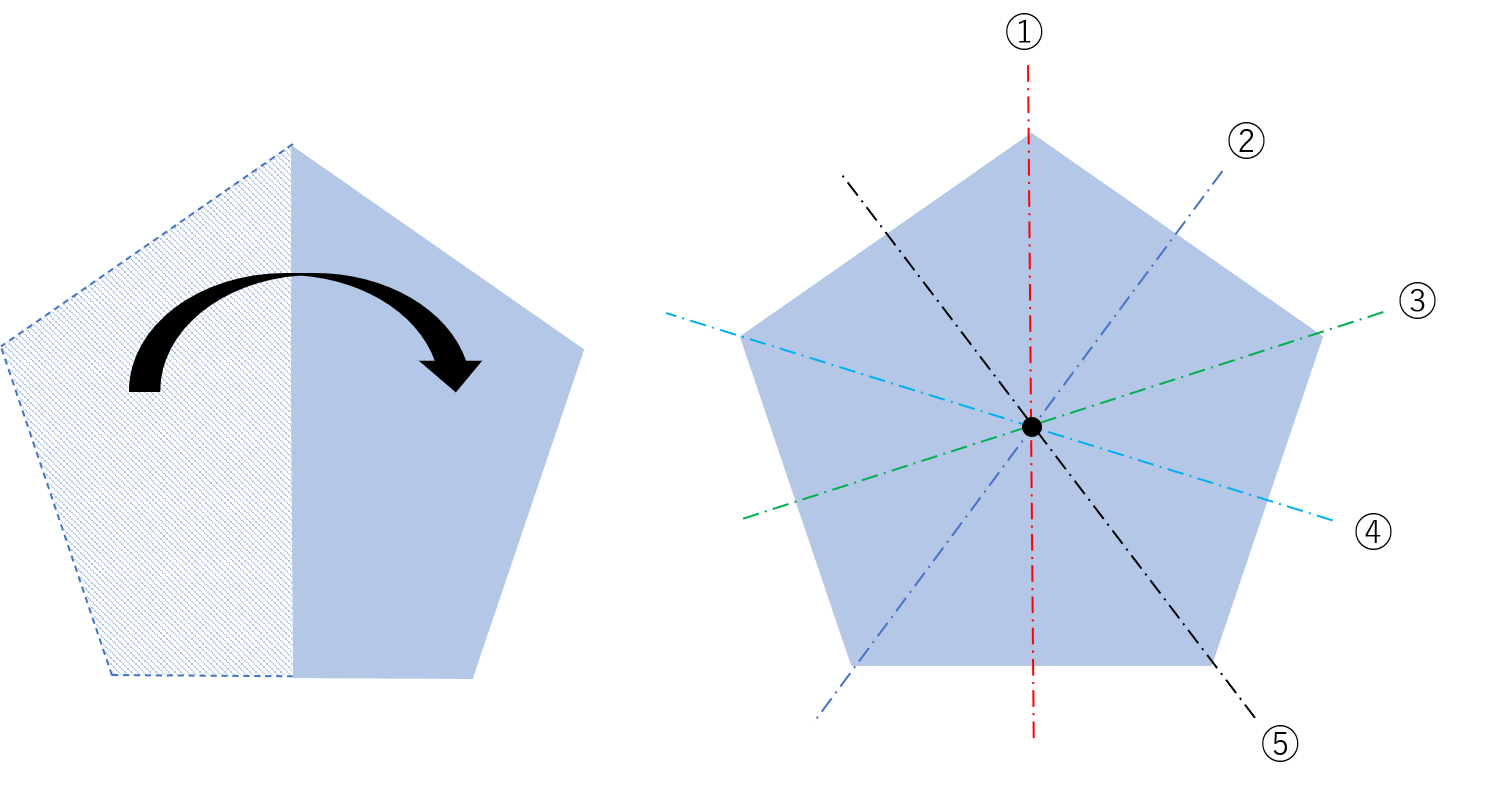
この図形は対称軸を真ん中に取るとピッタリ重なるように折りたためるので、点対称です。
対称軸とは、折りたたむときに折り目となる直線のことです。
また、この五角形の他の対称軸を探すと、合計で\(5\)つの対称軸が取れます。
そして、これらの対称軸が全て\(1\)点で交わっていることも分かります。
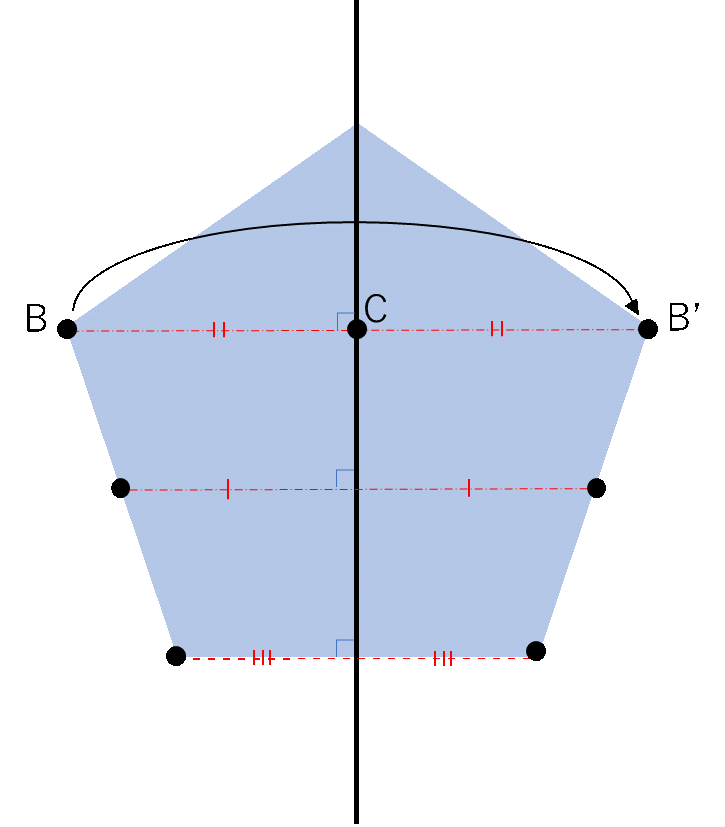
また、点対称で見たように対応する点についても考えてみましょう。
線対称は対称軸で図形を折り返すことを考えるので、上図の対称軸の場合Bの対応する点はB’になります。
次に、図形上の点(B)とそれに対応する点(B’)を結ぶ線を考えます。
そして、対称軸とB・B’を結ぶ線(BB’)の交点をCと置きます。
点対称と似たように、BC=B’Cとなります。また、∠BCB’も\(180\)°です。
BC=B’Cであったように、線対称な図形では図形上の点(B)から対称軸との交点(C)の距離は対応する点(B’)から交点(C)の距離と等しくなります。
また、∠BCB’が\(180\)°であったことから、対称軸と対応する\(2\)点を結んだ線は常に直角に交わります。
線対称な図形には、対称軸で折り合わせるとピッタリ重なることの他にこのような性質があります。
まとめ
この記事では、点対称であれば対称の中心で\(180\)°回転させても同じ図形であり、線対称であれば対称の軸で折り合わせるとピッタリ重なることを学びました。また、それぞれ図形上の点とそれに対応する点を考えると、距離や角度に関する性質を見つけることができました。
実は今回点対称の例として使用した図形は線対称になりますが、線対称の例として使用した図形は点対称になりません。また今回の例にはありませんが、反対に点対称ではあるが線対称ではない場合も存在します。アルファベットの「N」などがその一例です。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/須藤>















