多項式とは【算数からやさしく解説】

多項式とは

多項式（たこうしき）とはざっくり言うと、掛け算でできたかたまりを足し引きしたものです。
もう少し詳しく言うと、多項式は単項式（たんこうしき）の和（足し算）で表される式のことです。
例としては、\(3x+2y+4zやa^2-2b\)などですが、多項式について知るためには単項式について知る必要があります。
また、よく間違われる整式などとの違いについても解説していきたいと思います。

↓↓↓動画で見たい方はこちら↓↓↓

単項式と多項式

単項式について説明する前に項について説明したいと思います。
項とは数や文字、または数と文字の積（かけ算）でできたかたまりのことで、例えば、\(2,a,-5a,\frac{b}{3}(=b×\frac{1}{3}),xyz\)などが項になります。（符号を含む）
この項についてわかると後の単項式や多項式についてはすぐに理解できます。
「単」体の「項」でできた式、つまり、項が一つのみの式を単項式と言います。先ほどの項の例として挙げたものはすべて単項式です。
「多」くの単項式（「項」）でできた式、つまり、単項式がいくつか足し合わした式を多項式と言います。
ここで、単項式は\(-5a\)などのように\(-\)（マイナス）がついてもよいので、
\begin{align*}
a^2-2b=a^2+(-2b)
\end{align*}
と捉えることで、多項式は掛け算でできたかたまりを足し引きしたものと考えることもできます。
また、基本的に単項式と多項式をまとめて整式と言います。
まとめると、以下のようになります

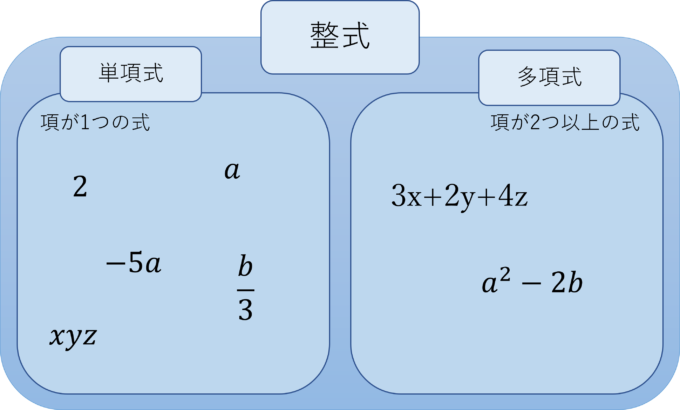
多項式のメリット

多項式や整式という言葉は中学だけでなく高校、大学と数学に触れるときにはよく出てくる言葉なので、多項式などを知っておくと今後の学習で活きてきます。

多項式の活用例

今回解説の中では出ませんでしたが、多項式同士の足し算かけ算などを使えば多項式を整数などと同じように扱うことができます。このようなことから基本対称式などを用いた様々な面白い性質などがあります。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

倍数の判定法【算数からやさしく解説】

<文/尾崎>

方程式のガロア群 深遠な解の仕組みを理解する　金 重明(著)　講談社