「ファッション×数学」

はじめまして！私、中村と申します。大学時代に物理学の対称性について研究しており、数学、物理学で学んだことを通して日常を見たり、応用したりすることが大好きです。そんな私にぴったりなBEYONDという数学イベントが開催されていましたので、レポートさせていただきます！

「数学とファッションって何の関係があるのだろう？」と皆さんは思っていませんか？
数学は科学の土台と言える学問ですが、実は数学的な物の見方は一見して全く異なる分野にも応用が出来ます。

第3回 BEYOND 今回のテーマは「ファッション×数学」
ファッションと数学はどのように融合されるのでしょうか？2017年9月15日(金)、Yahoo JAPAN オープンコラボレーションスペース「LODGE」にてエマリーエ代表 松居エリ様がご講演しました。

講演に先立ってBEYOND運営委員会代表の堀口さんより、ミニマルアートという20世紀に生まれた、新しいアートについてのご紹介がありました。

20世紀初頭に従来の「作者が意味を伝える」アートから、「鑑賞者がどんな意味を見出すか」というアートへの変革があったそうです。相対性理論における世界の見え方の変化がこのようなアートの変革へ影響を及ぼしたのではないか、というのが堀口さんの持論です。

堀口さんの熱いプレゼンで場が暖まったところで松居様にバトンタッチです！

松居様の講演内容は下記のようになっております。
【講演内容】
∞なぜ、数学と科学を取り入れたデザインをしてきたか？
∞数学とは私にとって何なのか？
∞研究者とのコラボレーションでどのように服を創るのか？
∞服とは何なのか？

元々、松居様は数学が出来なかったと言います。それなのに何故ファッションに数学を取り入れたのかという話について、松居様は過去に「直感だけでは創れない物があったから」と言います。その時に数学的思考、科学的思考が非常に大切だったそうです。
「思考と感性は敵対するものではなく内包し合う」と言う松居様のお言葉は、創作活動全般に当てはまる話だと感じました。

それでは実際に紹介された服を見ていきましょう！

対数螺旋×ファッション

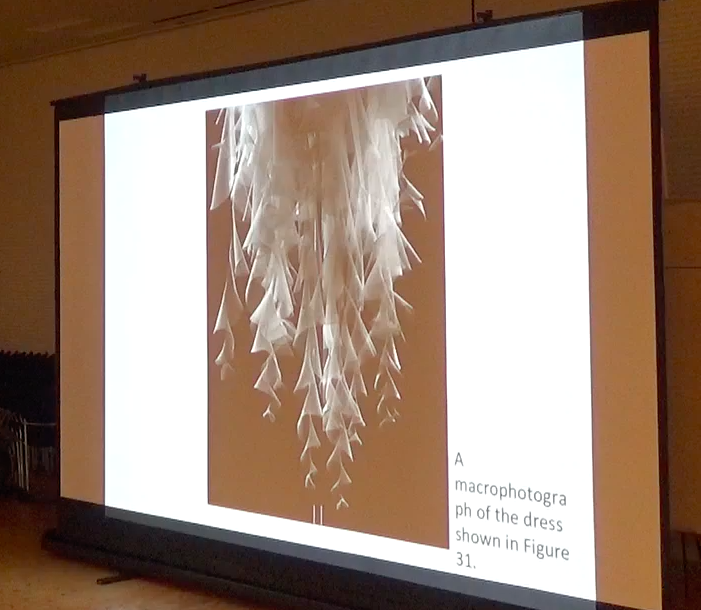
服で対数螺旋を表したとのこと。生地を余す所なく、切ったまま垂らしているそうです！

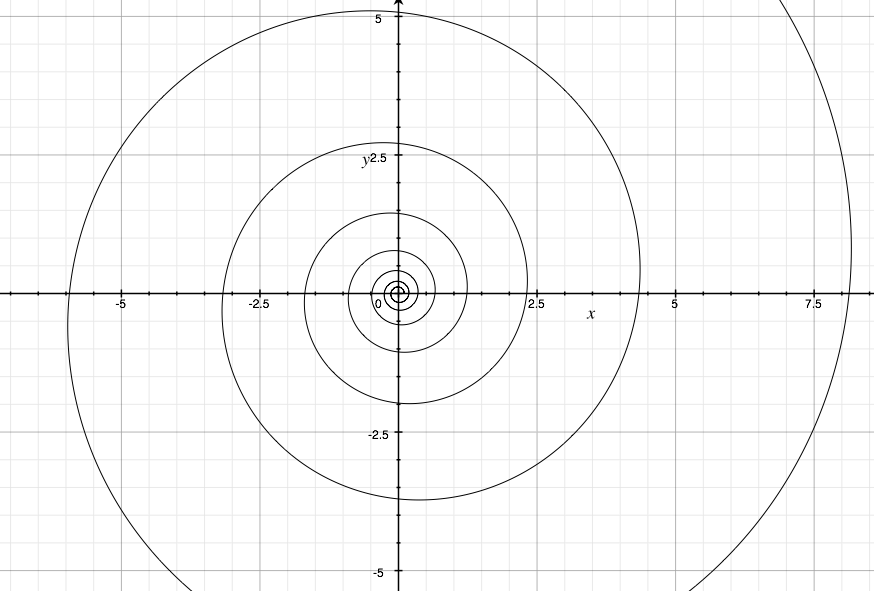
～対数螺旋とは？～
以下の図のような螺旋のことを言い、自然界ではオーム貝や渦巻銀河等に見受けることが出来ます。

フラクタル×ファッション

服の模様がシェルピンスキーのギャスケットを描いています。

～フラクタルとは？～
例えば木を見てみると、幹から出る枝の生え方と枝から出る枝の生え方の形が似ていることに気が付きます。
このように全体と部分の形が同じであるような図形をフラクタルと言います。フラクタルは他にも海岸線や宇宙の構造などありとあらゆる自然に見つける事が出来ます。

ロジスティック写像×ファッション

ロジスティック写像が描き出す模様をそのまま服にしたドレスです。

～ロジスティック写像とは？～
ロジスティック写像は生物の個体数の変動モデルを表します。また、有名な「カオス」という現象を表す式の一例ともなっています。計算機の世界では、このカオス現象をして疑似乱数の生成に応用がされています。

フィボナッチ数列×ファッション

脳にとって規則性のあるものは美しいではないか？という発想から生まれたドレス。ここで松居様が仰った規則とはフィボナッチ数列のことを指します。

～フィボナッチ数列とは？～
フィボナッチ数列はひまわりの種や松ぼっくりなど自然界の様々な所で見つける事が出来ます。
また有名な黄金比とも関係があり、連続するフィボナッチ数の比は値が大きくなるにつれて黄金比に近づいていきます。

トポロジー(位相)×ファッション

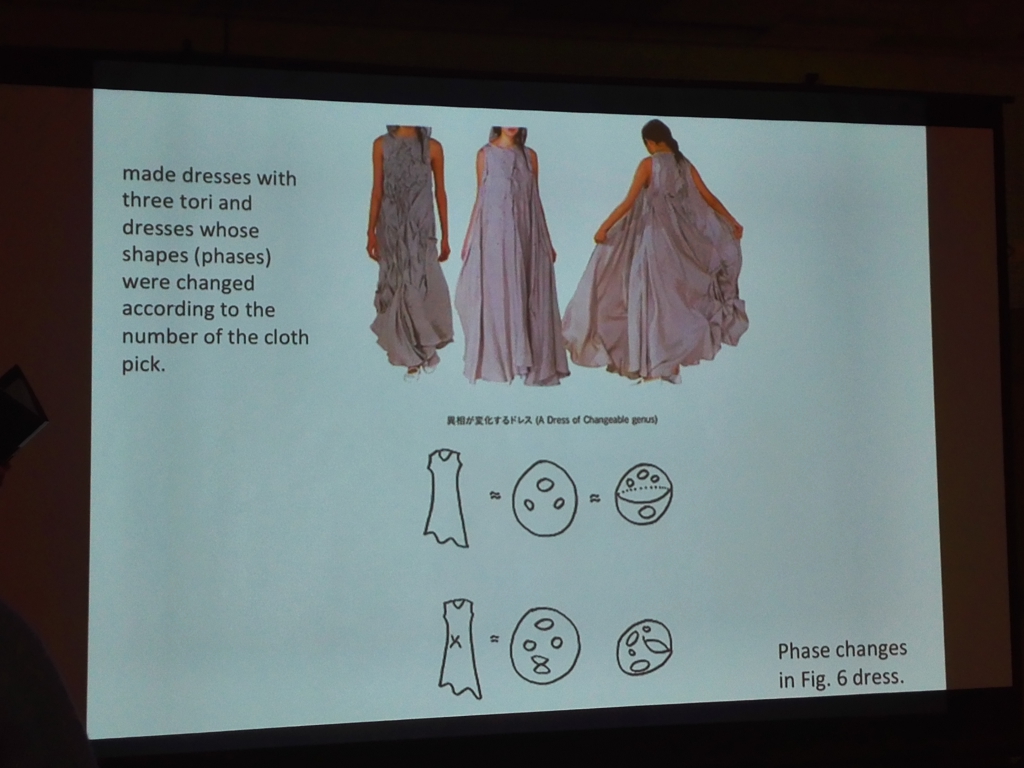
トポロジーでは対象に開いている穴の数で物を分類します。そこに発想を得た、位相が変化していくドレスです。

～トポロジーとは？～
トポロジーは講演にもあった通り「柔らかい幾何学」と呼ばれる事もあります。対象を切断すること無く、伸ばしたり捻るなどをして連続的に変形可能かどうかを主に考える幾何学の一分野です。

～位相とは？～
「対象 A と B は位相が同じ(同相である)」とは対象 A と対象 B が連続変形(切断無しの伸び縮み)で移り合える事を意味します。例えば、ドーナツとコップは同相です。

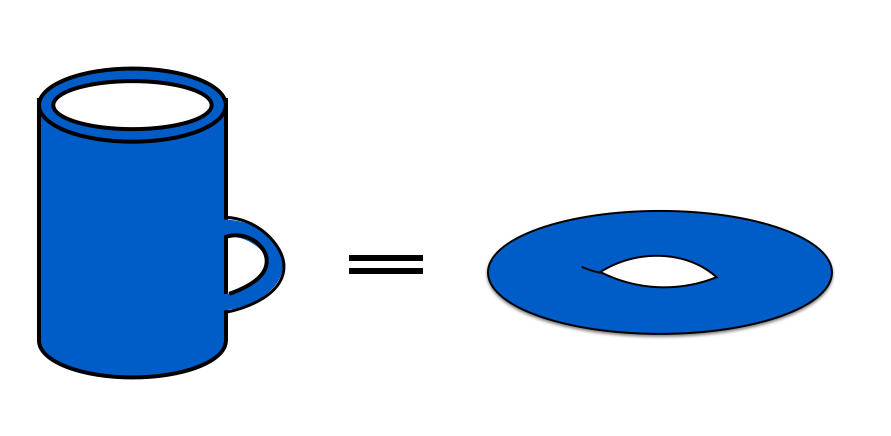
結び目理論×ファッション1

スライドの女性が持っているものは数学の結び目です。

結び目を動かすだけで、様々な身体の大きさにフィットしてしまうドレスです。

それまで角度を重要視していたが、幾何学のトポロジーの考え方そのものにインスピレーションを得て、角度と長さに捕らわれない服を結び目理論を用いて創る事が出来たそうです。さすが「柔らかい幾何学」！と思いました。トポロジーの考え方は、服だけでなく、製品のデザイン全般に応用できそうですね！

結び目理論×ファッション2

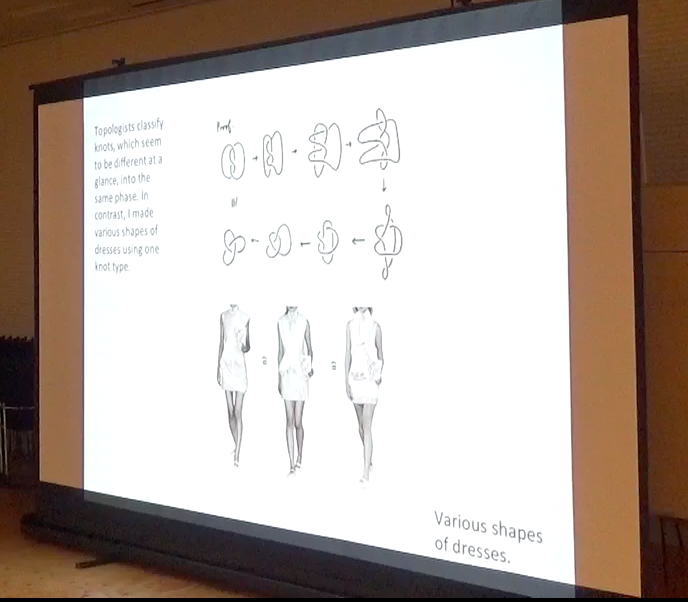
結び目としては同じですが、それを変形して色々な巻きつけ方をしたドレスです。

～結び目理論とは？～
結び目(輪っか)を分類するトポロジーの1分野を指します。
紐を切断すること無く変形して作れる結び目を同じものとみなすので、例えば結び目理論では以下の結び目を同じものとみなします。

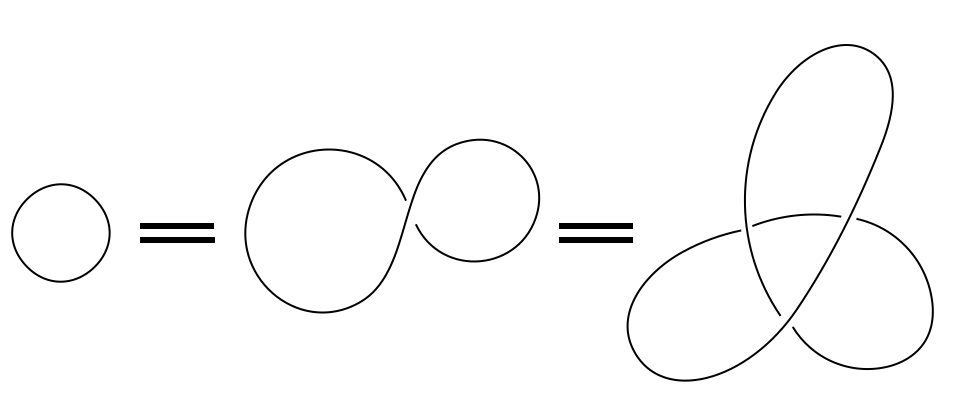
しかし、以下の結び目は切断すること無く移り合えない為、同じものではありません。

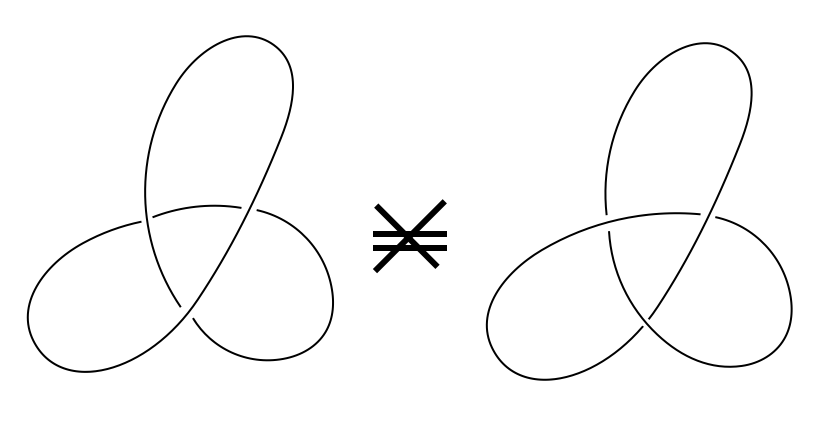
脳×ファッション

これは脳の形をスケッチし、服にしたドレスです。このように、何らかの対象があってそれをそのまま服にする事もあるそうです。

螺旋×ファッション

折り紙博士であり数学者でもある川崎敏和先生の作品である二重螺旋を参考にされたドレスです。

松居様は直感で美しいと感じた数学をファッションに取り入れ、これが良いのではないか？という仮説から実験を行うとの事です。
ファッションという感性の部分と仮説と実験数学の理論を組み合わせる松居様。実験も数学の理論もファッションも良いと思った物をすぐに取り入れる松居様の姿勢を見習いたいと思いました。

フラクタル、トポロジー、結び目理論、ロジスティック写像、フィボナッチ数列、対数螺旋など多岐に渡る分野の数学をファッションと融合させた松居様のご講演はこれぞまさに BEYOND！というものでした！
今回の講演の内容をお聞きして、数学×音楽、数学×家具、数学×絵画等色々な芸術活動、創作活動に数学からBEYONDしていけるという未来を私は感じました。

《懇親会の様子》
懇親会ではお酒と食事を囲んで、アート関係の方、数学関係の方が交流をして楽しく議論をすることが出来ました。

私は数学そのものも好きですが、数学を通して世界の見方がが広がる感覚を感じるととても嬉しい気持ちになります。
数学とファッションの融合から生まれる松居様の創られた服は、数学の応用としての１つの形と言えるでしょう。
実際、数学とサイエンスを取り入れることで様々な造形が生まれたそうです。
科学とファッション、アートが融合されている沢山の服をスライドで見せて頂いていると服そのものが数学の具体例であるように感じました。服から数学を学べるようでとても面白かったです。

第4回 BEYOND のテーマは「VR×数学」(予定) 今年12 月に開催予定とのことです。次回もお楽しみに！！

（文／中村俊介）