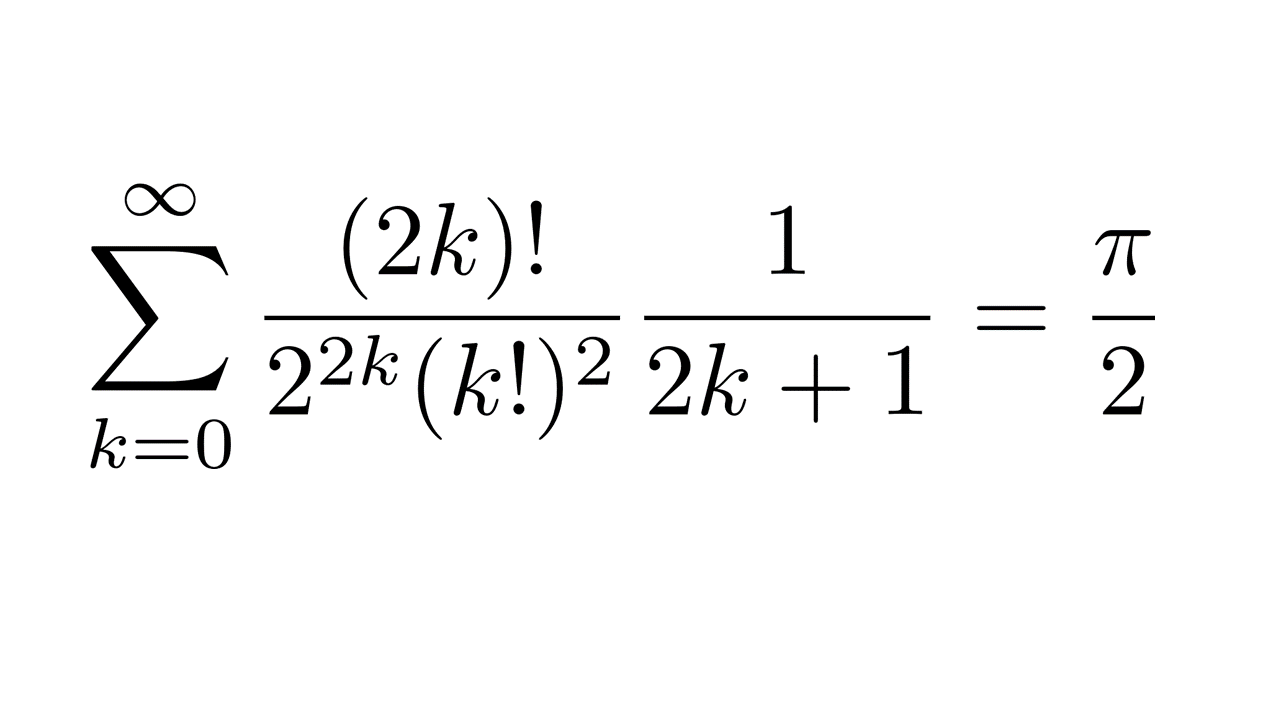好きなπの定義式
公開日
2020年10月8日
更新日
2020年10月8日

動画で見たい方はこちら↓↓↓
数学教室和(なごみ)講師の松中です。
以前、マスログ「やばそうな数式(意味偏)」において、
という一文を書かせていただきました。
今回はこちらのお話を少し深堀し、私の好きな\(\pi\)の定義を紹介したいと思います。
円周率\(\pi\)の定義
実は私は10年前の新卒時代に、以前勤めていた職場の忘年会の余興で「好きな\(\pi\)の計算式ベスト10」を発表したことがあります。
事前にスケッチブックを購入し、太ペンで\(\pi\)の等式を10個ランキング形式で記載しておき、職場の上司、先輩、同期の前でベスト10からベスト1まで順番に発表していく予定でした。
しかし当時は数学とは全く関係のない職場であったため、ベスト6くらいまで発表したところで当時の事業部長に「それ以上は発表したらダメだ」と止められてしまいました。今思うと私はKYだったのかもしれません。
さて、当時発表したのは「好きな\(\pi\)の計算式ベスト10」ですが、これは「好きな\(\pi\)の定義式ベスト10」とも言い換えることができます。
「え?\(\pi\)の定義って円周と直径の比でしょ?」って思った方は正解です。円周率\(\pi\)はその名の通り、「円周と直径の比」です。それは間違いありません。しかし、円を用いて幾何的に定義されている\(\pi\)ですが、\(\pi\)は数学のあらゆる分野の数式にその姿を現します。その数式から「\(\pi=\)○○」の形に変形できれば、それを改めて\(\pi\)の定義として採用してよいわけです。
例えばマスログ(やばそうな数式)の中で、
\[
\prod_{k=1}^{\infty} \frac{4k^2}{4k^2 – 1} = \prod_{k=1}^{\infty} \left(\frac{2k}{2k – 1}\cdot\frac{2k}{2k + 1}\right) = \frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdots=\frac{\pi}{2}
\]
であることを紹介しました。このイコール\(=\)は厳密に成り立つので、この等式から逆に、
\[
\pi=2\times \frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdots
\]
として\(\pi\)を定義できるのです。もちろん\(\pi\)を上の式で定義すると、その値が「円周と直径の比」と一致することは別途証明する必要があります。
当時の私のベスト10は覚えていないのですが、例えば以下に紹介するような2つの定義式は必ず入っていたはずです。
ガウス積分による定義
\pi=\left(\int_{-\infty}^\infty e^{-x^2}dx\right)^2
\]
この\(\pi\)の定義はガウス積分と呼ばれる定積分 \(\displaystyle \int_{-\infty}^\infty e^{-x^2}dx=\sqrt{\pi}\)の両辺を二乗したものです。ガウス積分は曲線\(\displaystyle y=e^{-x^2}\)と\(x\)軸で挟まれる面積が\(\sqrt{\pi}\)であることを意味しています。
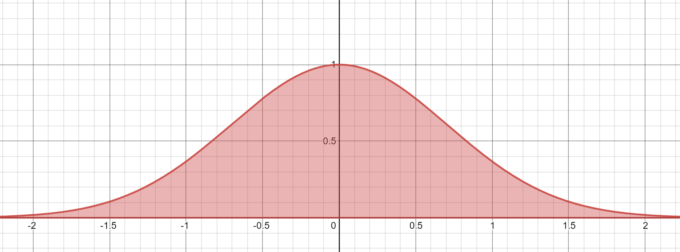
この定義の好きなところは、このガウス積分が物理や統計学など純粋数学の外の世界にもたくさん現れる重要な公式である、というところです。このグラフはどこかで見たことないでしょうか?そうです、統計学を勉強すると必ず出てくる正規分布のグラフです。標準正規分布の確率密度関数は、
\[
p(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
\]
と表せます。統計学をやっていると突如現れる\(\pi\)、その背景にはガウス積分があったのです。ガウス積分が統計学と\(\pi\)を結び付けています。
ゼータ関数\(\zeta(s)\)の特殊値による定義
\pi=\sqrt{6\times\zeta(2)}=\sqrt{6\sum_{n=1}^\infty\frac{1}{n^2}}=\sqrt{6\left(1+\frac{1}{4}+\frac{1}{9}\cdots\right)}
\]
この定義式は全ての自然数と\(\pi\)をシンプルで美しい形で結びつけています。これこそゼータ関数\(\zeta(s)\)のなせる業です。ゼータ関数\(\zeta(s)\)は\(s=2m\,(m:\text{自然数})\)でとる値が完全に知られており、
\[
\zeta(2m)=(-1)^{m+1}\frac{2^{2m-1}B_{2m}}{(2m)!}\pi^{2m}
\]
となります。\(B_{n}\)はベルヌーイ数と呼ばれる有理数の数列であり、\(\zeta(2m)\)が\(\text{(有理数)}\times \pi^{2m}\)の形で表せるところが最高に面白いです。
このことから上の定義式をちょっと高尚にして、
\[
\pi=\left((-1)^{m+1}\frac{(2m)!}{2^{2m-1}B_{2m}}\sum_{n=1}^\infty\frac{1}{n^{2m}}\right)^{\frac{1}{2m}}
\]
としてもよいです。\(m\)は任意の自然数なので一気に可算無限個の\(\pi\)の定義式を得ることができました!
一番好きな\(\pi\)の定義式
さて、本記事で私が紹介したかった今時点の私が一番好きな\(\pi\) の定義式は、
\[
\left\{\begin{align}
\frac{{\rm d}}{{\rm d}\theta}s(\theta)&=c(\theta)\\
\frac{{\rm d}}{{\rm d}\theta}c(\theta)&=-s(\theta)\\
s(0)&=0\\
c(0)&=1
\end{align}\right.
\]
で定まる関数\(s(\theta)\)、\(c(\theta)\) に対して、
\[
\pi=\inf\left\{\theta>0|s(\theta)=0\right\}
\]
と定義する。
です。
この定義式が好きな理由はシンプルであるということに尽きます。 \(e\) もベルヌーイ数\(B_n\)も \(\displaystyle \sum\) も \(\displaystyle \int\) も出てきません。出てくる数は\(0\)と\(1\)というとても基本的な数だけです。こんな単純な数式からπが出てくるとは到底信じられないです。
これは微分方程式と呼ばれるものですが、数学の世界では微分方程式を用いて新しい関数を定義することがあります。
この\(\pi\)の定義式では微分方程式で\(s(\theta)\)、\(c(\theta)\)という2つの関数を定義しているわけですが、お察しの通り\(s(\theta)\)、\(c(\theta)\)は\(\sin{\theta}\)、\(\cos{\theta}\)と一致します。
つまり高校の時に次の図のような単位円周上の座標として定義された\(\sin{\theta}\)、\(\cos{\theta}\)を別の形で再定義している式とも見れるのです。
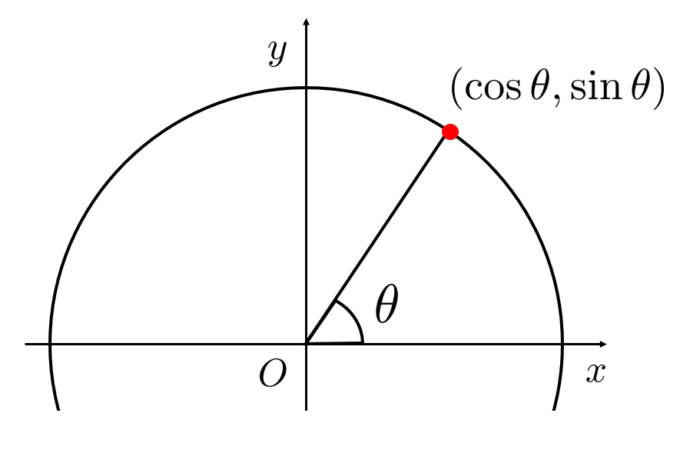
\(\sin{\theta}=0\) の解は \(\theta=n\pi\) だったので、正の最小解は\(\theta=\pi\)になるということで、\(\displaystyle \pi=\inf\left\{\theta>0|s(\theta)=0\right\}\) と定義しているわけです。
定義式を眺めてみましょう。
\[
\left\{\begin{align}
\frac{{\rm d}}{{\rm d}\theta}s(\theta)&=c(\theta)\\
\frac{{\rm d}}{{\rm d}\theta}c(\theta)&=-s(\theta)
\end{align}\right.
\]
が意味しているのは、\(s(\theta)\)の増加量は\(c(\theta)\)によって決まり、\(c(\theta)\)の増加量は\(s(\theta)\)によって決まるということです。最初\(s(0)=0\)、\(c(0)=1\)と出発点が与えられており、互いに手を取り合いながら一歩ずつ前に進みながら\(\theta=0\) 以外の\(\theta\) での値が決まっていくのです。
微分方程式は難しそうなイメージがありますが、多少の誤差を許してもよいのであれば簡単に数値計算をすることができるので、実際に計算してみましょう。
与えられた微分方程式部分は近似的に
\[
\left\{\begin{align}
\Delta s(\theta) &\approx c(\theta)\Delta \theta\\
\Delta c(\theta) &\approx -s(\theta)\Delta \theta
\end{align}\right.
\]
と書くことができます。\(\Delta\) は微小の変化量を表しており、これをもっと書きかえると、
\[
\left\{\begin{align}
s{(\theta+\Delta\theta)}-s(\theta) &\approx c(\theta)\Delta \theta\\
c{(\theta+\Delta\theta)}-c(\theta) &\approx -s(\theta)\Delta \theta
\end{align}\right.
\]
となります。\(\Delta\theta\)は\(0.01\)などのような小さい正の実数です。
この式で例えば、\(\theta=0\)、\(\Delta\theta=0.01\)とすると、
\[
\left\{\begin{align}
s(0.01)-s(0) &\approx c(0)\cdot 0.01\\
c(0.01)-c(0) &\approx -s(0)\cdot 0.01
\end{align}\right.
\]
となり、\(s(0)=0\)、\(c(0)=1\)から、\(s(0.01)=0.01\)、\(c(0.01)=1\)と計算できます。次に同様に、\(\theta=0.01\)、\(\Delta\theta=0.01\)とすることで、
\[
\left\{\begin{align}
s(0.02)-s(0.01) &\approx c(0.01)\cdot 0.01\\
c(0.02)-c(0.01) &\approx -s(0.01)\cdot 0.01
\end{align}\right.
\]
となり、先ほど計算した\(s(0.01)=0.01\)、\(c(0.01)=1\)から、\(s(0.02)=0.02\)、\(c(0.02)=0.9999\)と計算できます。以下同様に同じ計算を繰り返すことで、次々に\(s(\theta)\)、\(c(\theta)\)の値が分かっていきます。先にも述べた通り、この計算は近似計算であることには注意してください。\(\Delta\theta\)を\(0.001\)、\(0.0001\)と\(0\)に近づけていくことでその近似の精度は高まり、\(s(\theta)\)、\(c(\theta)\)の真の値に近づいていきます。
このように計算を続けていくと、\(s(\theta)\)が正から負に変わる瞬間があります。その時の\(\theta\) が\(\pi\) の近似値になっているのです。
\(\Delta\theta=0.01\)として、実際にエクセルで計算してみました。
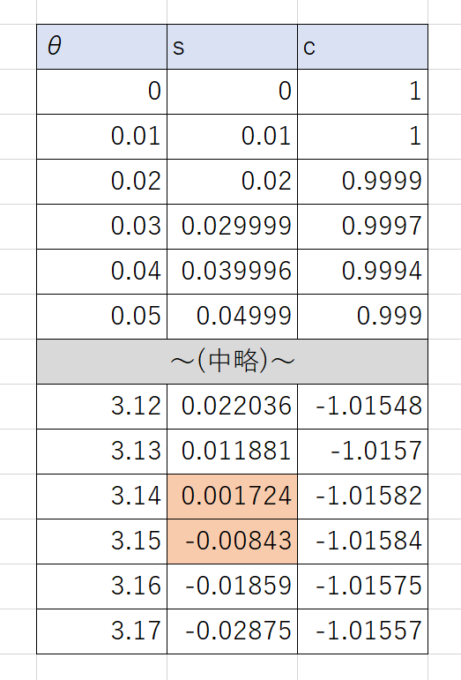
たしかに、\(\theta\)が\(3.14\)を超えると\(s(\theta)\)が負に変わることが分かります!\(\Delta\theta\)を\(0\)に近づけることで、より高い精度で\(\pi\)を計算することができます。
\(\pi\)というとてつもなく神秘に満ちた数を、エクセルで一から簡単に計算できます!みなさんもぜひやってみてください!
<文/松中>