平均値と中央値の差は標準偏差以下になることの証明

ロマンティック

公開日

2021年7月10日

更新日

2021年7月10日

こんにちは。和からの数学講師の岡本です。今回は、前回お話した「平均値と中央値の差」に関する話題です。

実はこの2つの指標は、必ずそのデータの標準偏差以下になるということを紹介しました。今日はそのことを「数学を使って」証明していこうと思います。

この記事の主な内容

１．復習

前回はいろんなデータに関して、平均値と中央値の差が標準編差以下になることを確認しました。果たしてどんなデータに対しても成り立つのでしょうか？まずは、この性質の意味からお話します。
「平均値と中央値の差が標準偏差以下である」とは、言い換えると、平均から±標準偏差広げたエリア内に必ず中央値が入っていることを意味します。

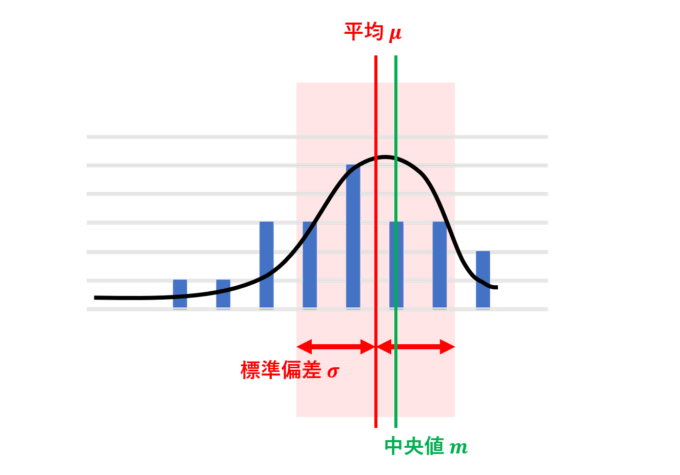
図のように、データの平均値を $\mu$ , 中央値を $m$ , 標準偏差を $\sigma$ とすると、示したいのは以下の不等式です。

$\begin{align*} |\mu-m|\leq \sigma. \end{align*}$

２．不等式の証明に使う道具

次に、不等式を示すのに必要な道具をそろえておきましょう。まずは利用する不等式についてです。
①三角不等式： $n$ 個の実数 $a_1, a_2, \ldots, a_n$ に対し次が成り立つ。

$\begin{align*} |a_1+a_2+\cdots+a_n|\leq |a_1|+|a_2|+\cdots+|a_n|. \end{align*}$

これは、「寄り道すると遠くなる」を表す三角不等式と呼ばれる不等式です。

②コーシー・シュワルツの不等式： $2n$ 個の実数 $a_1, a_2, \ldots, a_n$ と $b_1, b_2, \ldots, b_n$ に対し次が成り立つ。

$\begin{align*} (a_1b_1+a_2b_2+\cdots+a_nb_n)^2\leq (a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2). \end{align*}$

これらの不等式は証明なしで使っていくことにします。また不等式に関しては以下のマスログで詳しく解説しているので、興味のある方は是非ご覧ください。

さらに、もう一つ必要な道具があります。
③中央値の特徴： $n$ 個の量的データ $x_1, x_2, \ldots, x_n$ に対して中央値を $m$ とし、次の関数を定義する。

$\begin{align*} f_2(x):=\sum_{i=1}^{n}|x_i-x|. \end{align*}$

このとき、 $x=m$ で $f_2(x)$ は最小値をとる。

このような中央値の性質に対しては以下のマスログで詳しく解説しています。併せてご覧ください（下記マスログにあわせて $f_2(x)$ としました）。

３．不等式の証明

$n$ 個の量的データ $x_1, x_2, \ldots, x_n$ に対して平均値を $\mu$ , 中央値を $m$ , 標準偏差を $\sigma$ として話を進めましょう。
[ステップ１] まずは $|\mu-m|$ から三角不等式を使って評価していきます。

$\begin{align*} |\mu-m|&=\frac{1}{n}|(x_1+\cdots+x_n)-nm|\\ &=\frac{1}{n}|(x_1-m)+\cdots+(x_n-m)|\\ &\leq\frac{1}{n}(|x_1-m|+\cdots+|x_n-m|)\\ &\leq\frac{1}{n}(|x_1-\mu|+\cdots+|x_n-\mu|). \end{align*}$

最後の不等式は、 $f_2(x)$ が $x=m$ で最小であることを用いました。
[ステップ２] 次に少しテクニカルですが、 $a_i=1, b_i=|x_i-\mu|$ として、コーシー・シュワルツの不等式を考えます。

$\begin{align*} (|x_1-\mu|+\cdots+|x_n-\mu|)^2\leq(1^2+\cdots+1^2)(|x_1-\mu|^2+\cdots+|x_n-\mu|^2) \end{align*}$

ここで、両辺に平方根を取ると

$\begin{align*} |x_1-\mu|+\cdots+|x_n-\mu|&\leq\sqrt{n(|x_1-\mu|^2+\cdots+|x_n-\mu|^2)}\\ &=n\sqrt{\frac{1}{n}(|x_1-\mu|^2+\cdots+|x_n-\mu|^2)}\\ &=n\sigma. \end{align*}$

この結果と[ステップ１]の不等式を併せることで

$\begin{align*} |\mu-m|\leq\frac{1}{n}(|x_1-\mu|+\cdots+|x_n-\mu|)\leq\frac{1}{n}n\sigma=\sigma. \end{align*}$

となり、示したい不等式が得られました。

４．さいごに

いかがでしたでしょうか？数学を使うことによって、どんな量的データに対しても、一般に平均値と中央値の差が標準編差以下になることが証明されました。数学は偉大ですね!このように数学は統計学をはじめ、様々な科学の世界に貢献してきています。特に統計学では、数学がわかるとデータの捉え方や扱い方など理解の質が変わります！皆さんもぜひ数理統計の世界へ挑戦してみてはいかがでしょうか！数理統計学のオススメ書籍をいくつかピックアップしておきます。

数理統計学―基礎から学ぶデータ解析鈴木武(著), 山田作太郎(著) 内田老鶴圃