モデルプラン：【発展】110分×15回
楕円曲線入門
公開日
2021年6月10日
更新日
2021年8月8日
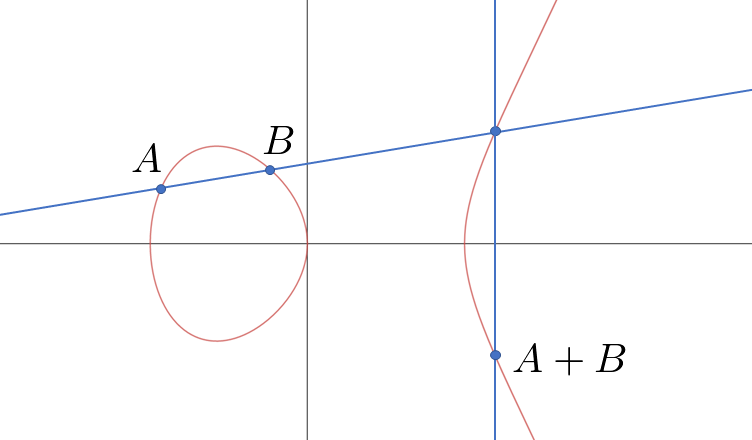
楕円曲線とは、フェルマーの最終定理を導くことになった志村-谷山予想や、ラングランズ予想、虚数乗法論など数学の様々な分野に登場する基本的なアイテムです。最近では、暗号理論との関係でも注目されています。
受講内容
テキスト「楕円曲線論入門」の第一章から三章の解説をします。
第一章 「幾何と算術」・・・楕円曲線を定義し、楕円曲線に群構造を導入します。
第二章 「有限位数の点」・・・楕円曲線上の有限位数の点（何倍かすると単位元になる点）の性質を調べる
第三章 「有理点のなす群」・・・非特異楕円曲線の有理点のなす群が有限生成であること（Mordellの定理）の証明をする
※「楕円曲線論入門」は第六章までありますが、本講座では前半の第三章までを対象とします。
※内容はお客様のご要望等によって変更することがあります。
受講対象
・楕円曲線に興味のあるが、一人では学習の継続が難しい方
・フェルマーの最終定理の証明や志村-谷山予想、ラングランズ予想に興味のある方
必要な数学知識
発展
モデルプラン
【110分×15回】
・3次曲線の書き方、3次曲線に群構造を入れる、3次曲線が群になる条件
・射影幾何、Weierstrassの標準形、非特異になる条件
・加法公式、２倍公式
・位数２、3の点、実数体上の楕円曲線、複素数体上の楕円曲線
・Weierstrassのp 関数
・3次式の判別式、Nugell-Nutsの定理
・Nugell-Lutsの定理の証明
・Nugell-Lutsの定理の応用、Mazurの定理
・Mordellの定理
・Mordelllの定理の証明（アウトライン）
参考テキスト
