楕円曲線入門(有限体上の3次曲線、虚数乗法編)
公開日
2021年8月8日
更新日
2021年8月8日

本講座では、「有限体上の3次曲線」と「虚数乗法」の基礎を学びます。また、ガロア理論の初歩についても同時に勉強していきます。
第4章「有限体上の3次曲線」では、x^3+y^3+z^3≡0 (mod p)(pは素数)の解の個数をガウスの方法を用いて決定します。ガウスは、有限体上の2次式の研究の後、3次式についても研究をすすめ、特別な3次式について解の個数を決定しました。ガウスの後、有限体上の3次曲線(楕円曲線)の解の個数については、ヴェイユ予想(合同ゼータ関数に対するリーマン予想)として一般化され、最終的には楕円曲線のみならず極めて広い対象(非特異射影多様体)において成り立つことが、1974年ドリーニュにより証明されました。本セミナーで取り扱う3次曲線は、このヴェイユ予想の出発点となった最も基本的な3次式で、解の個数を具体的に決定します。つまり、ヴェイユ予想の最も簡単な具体例を学ぶことになります。
また、第6章「虚数乗法」では、ある特別な楕円曲線の等分点をガウス数体Q(√−1)に付加すると、Q(√−1)のアーベル拡大となることを証明します。また、逆に、Q(√−1)のアーベル拡大は、ある特別な楕円曲線の等分点を付加することによってできることも証明します。これは、いわゆる「クローネッカーの青春の夢」の最も簡単な例であり、同時に、類体論の簡単な事例とみることもできます。また、その証明にはガロア表現を用いていますので、ガロア表現の入門としても最適です。
更に、第6章では、ガロア理論の基礎を用いますので、第6章を読むまでにガロア理論の初歩についても併せて学んでいきます。(本セミナーではガロア理論は前提とはしません。)特定のテキストは用いませんが、本セミナーの前半に講師作成のプリントを用いてガロア理論に入門します。
このように、本セミナーでは、①ガロア理論の初歩、②(ヴェイユ予想の元になった)有限体上の3次式の解の個数の決定、③(クローネッカーの青春の夢や後に類体論につながる)Q(√−1)のアーベル拡大の構成について理解することを目標とします。
受講対象
・楕円曲線に興味のあるが、一人では学習の継続が難しい方
・ガロア理論、ガロア表現に興味がある方
・類体論の初歩を知りたい方
・クローネッカーの青春の夢に興味がある方
・フェルマーの最終定理、ラングランズプログラムに興味がある方
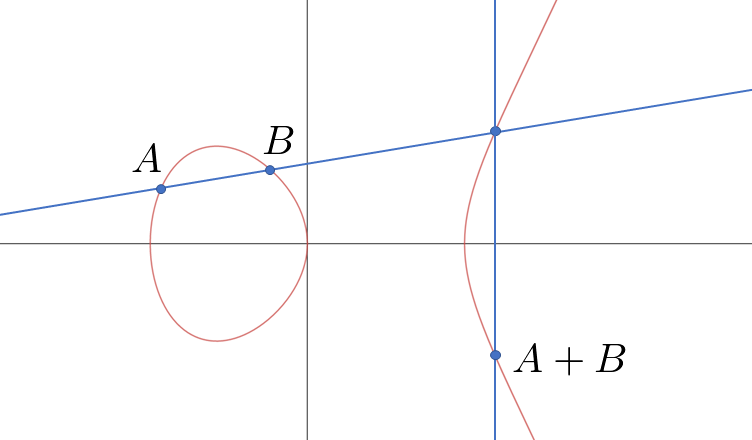
※群論の基礎については、ある程度の知識があることが望ましいです。また、楕円曲線が群をなすこと(「楕円曲線論入門」の第1章の内容)については前提とするものの、第2章、第3章の内容については必ずしも必要ありません。一部、第2章、第3章の内容を参照しますが、本講座において理解できるように解説を行う予定です。