「タンジェント」の不思議な等式とその証明③

公開日

2025年7月2日

更新日

2025年6月26日

こんにちは！和からの数学講師の岡本です。今回は、前回・前々回と続けて扱ってきた「タンジェントの不思議な等式」の証明シリーズの第3弾として、図形（幾何学）を用いた証明を紹介します。これまでの解析的アプローチとは異なる、美しく直感的な手法です。ぜひ一緒に体験してみてください。

この記事の主な内容

１．タンジェントの不思議な等式（復習）

まずは目標である“不思議な等式”について振り返ってみましょう。

まずは今回も、目標となる不思議な等式を確認しましょう。角度 \(\alpha, \beta, \gamma\) が \(\alpha + \beta + \gamma = \pi\) を満たすとき、次の等式が成り立ちます：

\begin{align*}
\tan \alpha \tan \beta \tan \gamma = \tan \alpha + \tan \beta + \tan \gamma
\end{align*}

前回は、複素数やオイラーの公式といった解析的な手法を用いてこの等式を証明しました。今回は、図形の性質に基づいた幾何学的な手法で証明してみます。ただし、証明上の都合により、角度 \(\alpha, \beta, \gamma\) がすべて \(0 < \alpha, \beta, \gamma < \frac{\pi}{2}\)（鋭角）である場合を考えることにします。

２．直角三角形を用意する

まず、3つの角度 \(\alpha, \beta, \gamma\) の和が \(\pi\) となるような状況を図形で表現します。以下の【図１】のように、順番に①から⑥までのステップで直角三角形を組み合わせて構成していきます。

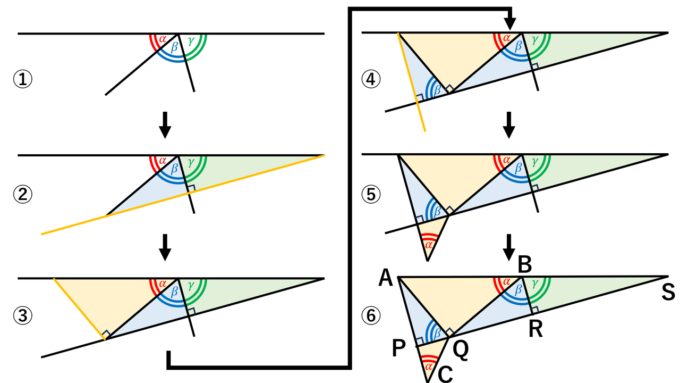
この図形から、三角形ABQと三角形QCPが相似、また三角形BQRと三角形QAPも相似であることがわかります。これらの相似関係を利用すると、辺BRとPCの長さが等しくなることが示され、これを 1 と設定しておきます。

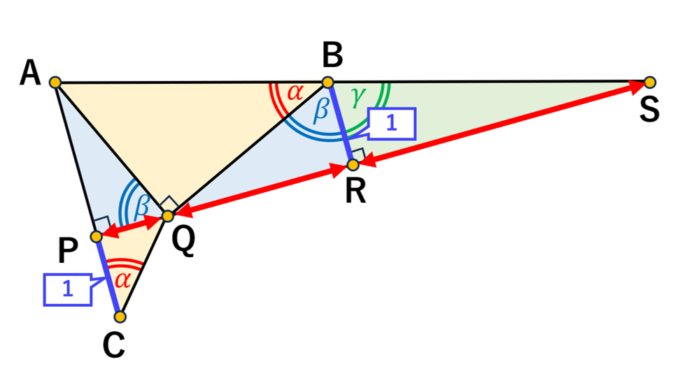
３．図形を用いた等式の証明

ここから、図形的にタンジェントの等式を証明していきます。図２の構造をもとに、それぞれの辺の長さを三角比で表現してみましょう。

\begin{align*}
PQ &= PC \times \tan \alpha = \tan \alpha \\
QR &= BR \times \tan \beta = \tan \beta \\
RS &= BR \times \tan \gamma = \tan \gamma
\end{align*}

よって、直線PSの長さは：

\begin{align*}
PS = PQ + QR + RS = \tan \alpha + \tan \beta + \tan \gamma
\end{align*}

一方で、PSは次のようにも表現できます：

\begin{align*}
PS &= \frac{PS}{AP} \cdot \frac{AP}{PQ} \cdot \frac{PQ}{PC} \cdot PC = \tan \gamma \cdot \tan \beta \cdot \tan \alpha \cdot 1
\end{align*}

これにより、

\begin{align*}
\tan \alpha + \tan \beta + \tan \gamma = \tan \alpha \tan \beta \tan \gamma
\end{align*}

という、まさに示したかった不思議な等式が得られました！代数ではなく図形の構成から導き出されるのがこの証明の面白い点です。

４．さいごに

一つの等式を、解析、代数、幾何と異なる手法で何通りも証明できるのは、数学の奥深さを感じさせる魅力のひとつです。今回紹介した図形を使った方法は視覚的で理解しやすく、数学の「美しさ」を感じられるものとなっています。今後もこうした証明の多様性や、数学に潜む構造の面白さを紹介していきますので、ぜひ引き続きご覧ください！

和からのセミナーで、数学をより深く楽しもう！

和からでは、こうした数学の奥深さやおもしろさを体験できる「高校数学の学び直しセミナー」を開講中です。全48回で、高校3年間分の数学を体系的に学び直すことができ、数学の背景や歴史、現代社会との関わりまで丁寧に紹介します。途中からの参加や動画での復習も可能なので、自分のペースでじっくり学びたい方にもおすすめです！

▼高校数学学び直しセミナーはこちら▼