78×72は?2桁の掛け算を一瞬で計算できる確率を上げる方法
公開日
2020年6月18日
更新日
2025年9月16日

こんにちは。和からの数学講師の岡本です。みなさんは「九九」って覚えていますか。1~9までの数の「掛け算の計算表」のことです。小学生の頃、苦労して覚えた方も多いのではないでしょうか。インドでは2桁同士の掛け算を覚えるとか。。。足し算や引き算、掛け算、割り算など社会人になっても不意に必要になることがあり、今でも苦労されてる方も多いようです。こうした大人のための算数については、以前のマスログで紹介していますので、是非参考にしてください。
実は先日、友人との会話の中で「78×72ってなんだっけ?」と聞かれました。「10×30=300」や「60×70=4200」などのように、本質的に九九の計算にゼロを2つ付けるだけの計算なら素早くこたえられそうですが、「72×78」はそれに比べてやや複雑です。みなさんはどれぐらいのスピードで答えられますか?
この記事の主な内容
1.72×78=5616
72×78の答えは5616です。実は、次の条件を満たすペアの掛け算が劇的に早く計算ができます!
素早く計算ができる2桁の数の条件
(条件2)1の位の数は足すとちょうど10になること。
例えば、(56, 54), (62, 68), (33,37) などは条件を満たしています。これらの掛け算は
$$56\times 54=3024 $$
$$62\times 68=4216$$
$$33\times 37=1221$$
となり一瞬で計算ができます。なにか規則に気づきましたか?実は下2桁に注目すると、1の位同士の掛け算がそのまま現れていることがわかります。
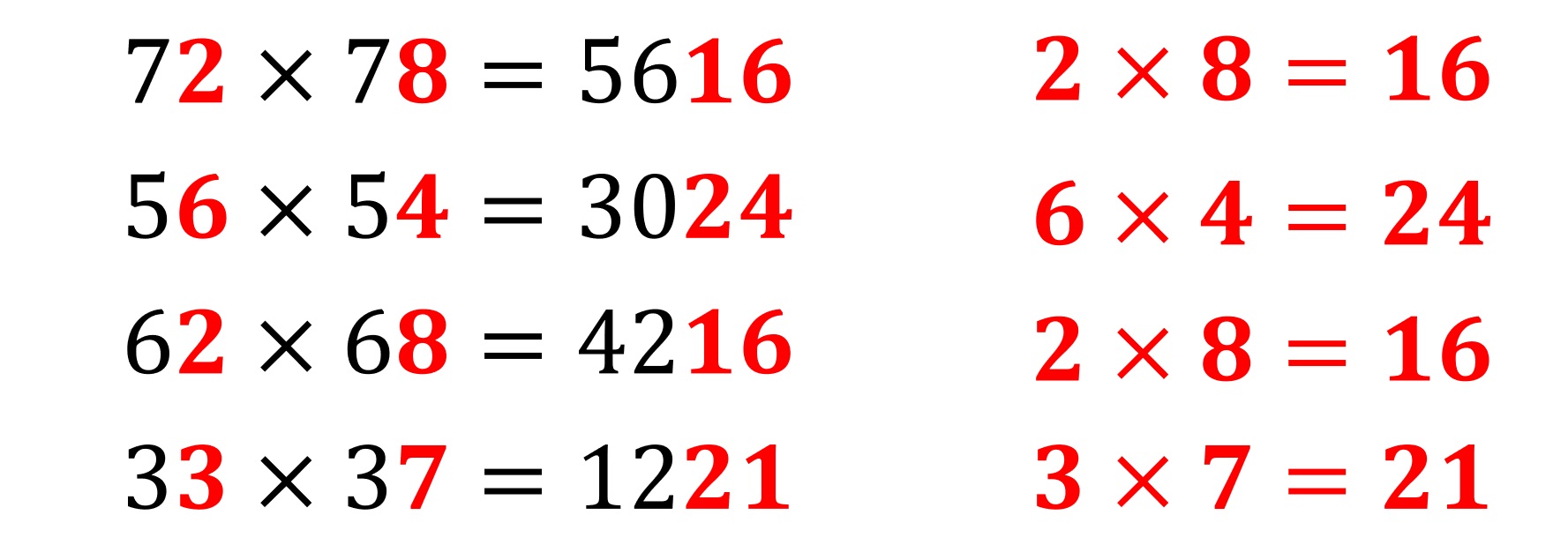
驚きの法則ですね!では上2桁はどう計算されるのでしょう?
もう一度観察してみます。「72×78」の場合、1の位の情報以外の情報は「7」しかありません。この情報だけで「56」をどう導き出すか。他の掛け算も同様に考えてみます。
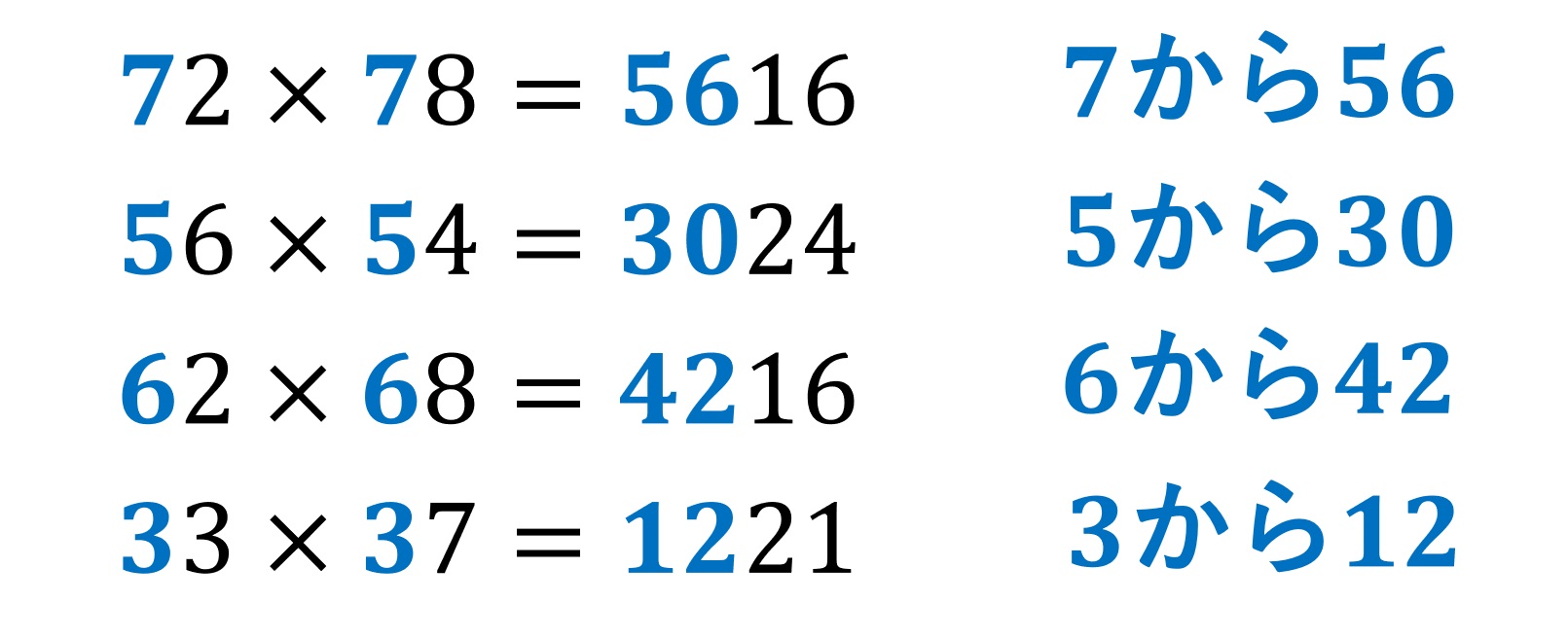
実は10の位の数とその数よりも1つ大きい数との掛け算で計算できます。例えば「7」の場合「7×8=56」。「5」の場合、「5×6=30」といった具合です。
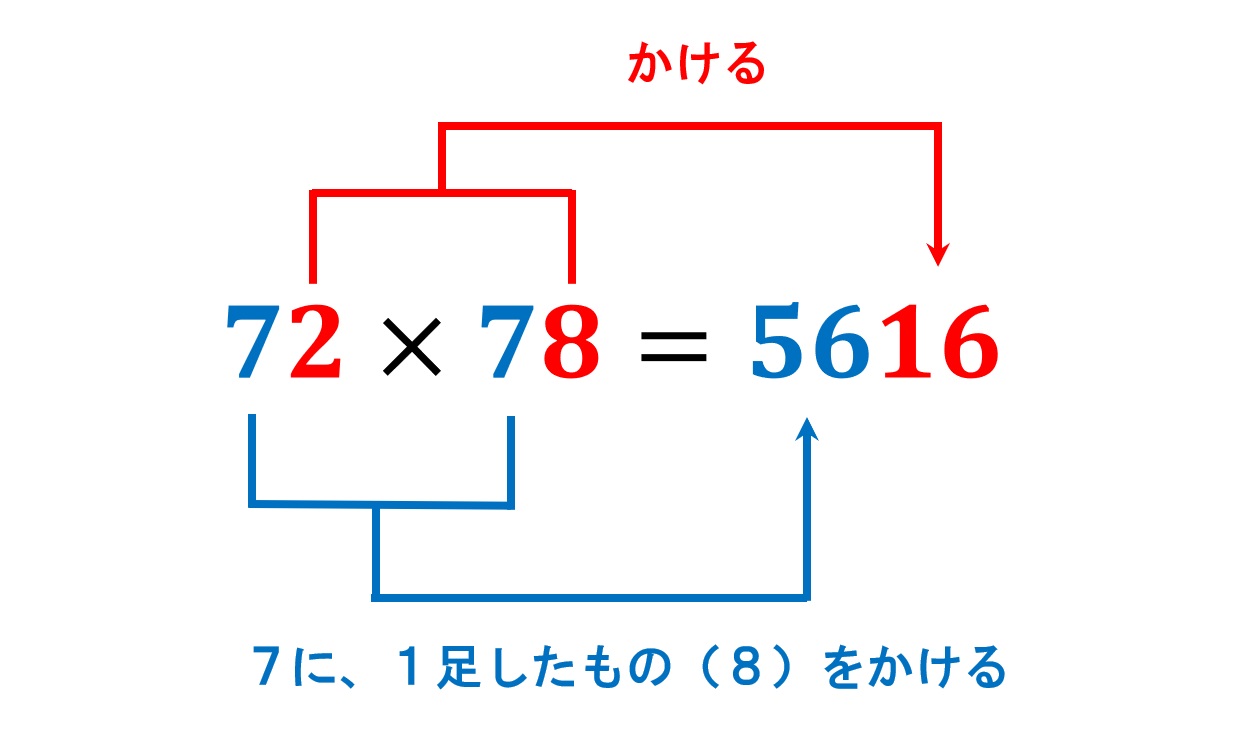
この魔法のような”裏技”を使えば、例えば「47×43=2021」と簡単に計算できます!
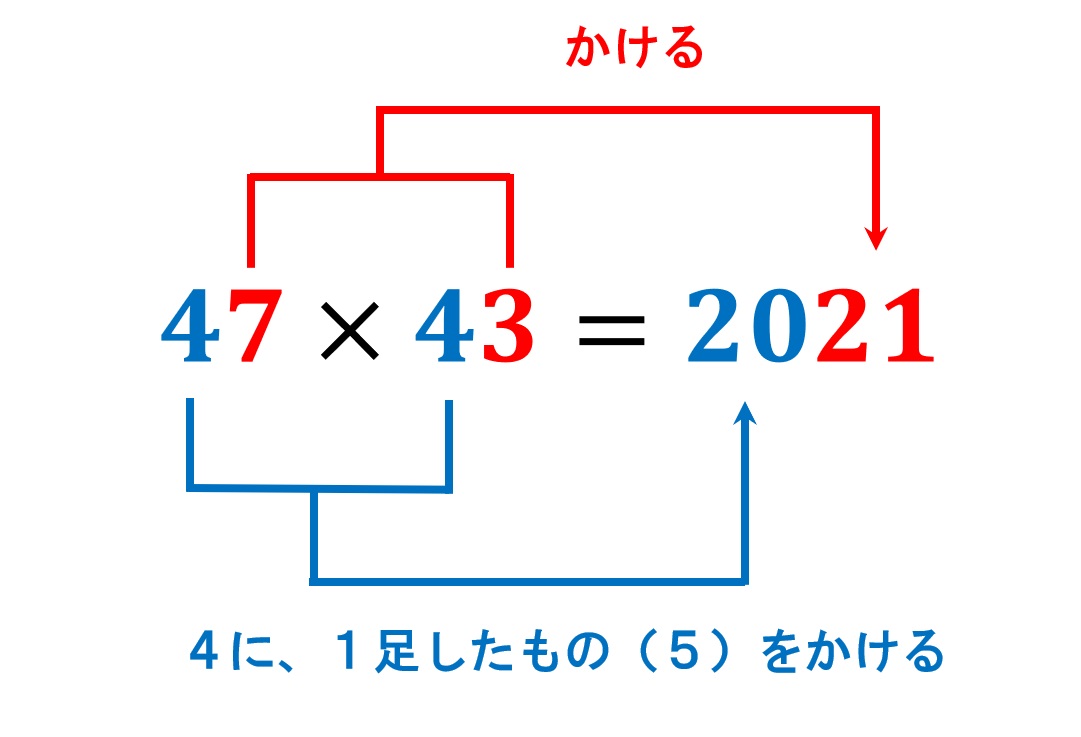
2.どうしてこんな計算で求められる?
なぜこれで正しい計算ができているのか気になる方のために、数学的な証明をしようと思います。文字の式を見るのが苦手な方は読み飛ばしていただいて構いません!
2つの条件を満たすペアは1~9までの数\(a\), \(b\)を使って
$$(10a+b, 10a+(10-b))$$
と一般的に表せます。これらの掛け算をそのまま行うと、
\begin{align*}(10a+b)(10a+(10-b))&=100a^2+10a(10-b)+10ab+b(10-b)\\
&=100a(a+1)-10ab+10ab+b(10-b)\\
&=100a(a+1)+b(10-b)\end{align*}
となり、たしかに上2桁は\(a\times (a+1\))で表され、下2桁は1の位同士の\(b\times (10-b)\)となっています。こうして条件を満たすペアに関して簡単に計算できることがきちんと証明されました!美しいですね!
3.素早く計算できる確率が2倍に!?
さて、この計算方法、早く試してみたいですよね!ということで、誰かに2桁×2桁の掛け算の問題を適当に出してもらいましょう。ただし、全ての場合についてこの方法で計算できるわけではありません!
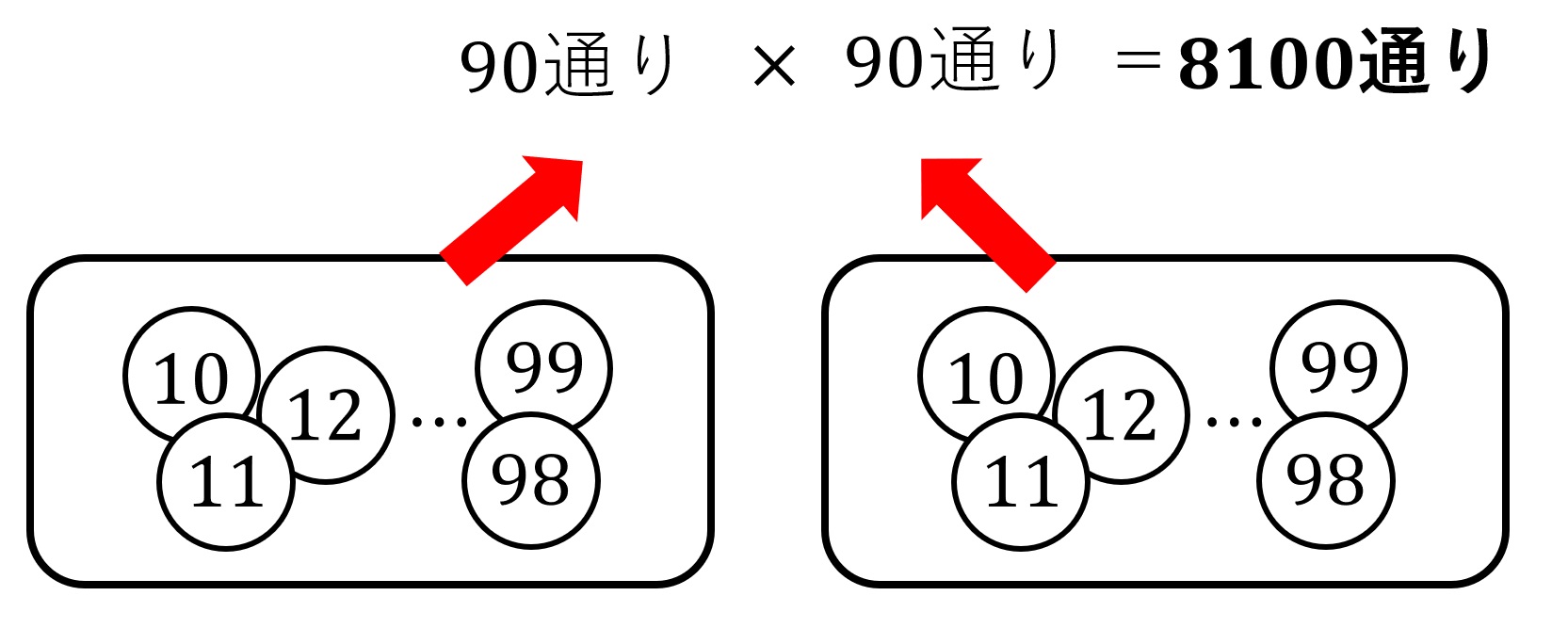
「2桁同士の掛け算がランダムに出題される」とは「10から99までの数をランダムに2つ選ぶこと」と同じです。このとき、全ての場合の数は90×90の8100通りです。
さてこの中でまず簡単で計算できるペアは「10×10」、「10×20」、…などの10の倍数ペア!これらは全部で9×9=81通り(九九と同じ)です。これまでだと81/8100=1%の確率でしか素早く答えることしかできなかったのですが、今回の”裏技”が利用できるペアが加わりました。どれだけ計算できる組み合わせが増えたか数えてみましょう。10の倍数以外の2桁の数(全部で90-9=81個)1つに対して、条件を満たす数は1通りに決まることがわかります。例えば「67」に対して条件を満たす数は「63」と決まってしまいます。このことから条件を満たす数のペアは全部で81通りであることがわかります。
以上の考察から、8100通りある2桁の数のペアの中で、瞬時に計算できるペアは81+81=162通りあることがわかりました。つまり162/8100=2%の確率で掛け算を瞬く間に計算することができるようになりました!
なんということでしょう!2倍になりました!この計算が必要になったらぜひ裏技を利用してください。
4.さいごに
ここでご紹介した計算方法ですが、いわゆるインド式計算法と呼ばれる、「なぜそうなるか」に基づき「早く」「楽に」計算する方法の特殊な場合です。今以上に瞬時に計算できる確率を高めたい方はインド式についても触れてみてはいかがでしょうか。なおインド式計算法に関するオススメの書籍として下記の本を挙げておきます。大人から子どもまで、楽しみながら計算を学ぶことができます!
和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つSPI対策まで、幅広く対応いたします。ご興味がある方はぜひ集団セミナー、無料個別カウンセリングにご相談ください。
<文/岡本健太郎>











