次元の呪い➁-高次元データの判別-

統計・機械学習トピック

公開日

2022年8月24日

更新日

2022年8月24日

↓↓↓動画で見たい方はこちら↓↓↓

みなさんこんにちは。和からの数学講師の伊藤です。今回も高次元データに関するお話ということで、機械学習の世界でよく扱われる「近傍法」という内容を扱っていきたいと思います。高次元データに対する諸問題（次元の呪い）の一つとして、これも有名な例になります。高次元の世界ならではの不思議な現象を、イメージから掴んでいただければと思います！

↓↓↓高次元データに関する記事はこちら

高次元データとは？-高次元統計解析-

この記事の主な内容

１．機械学習で使われるデータの判別問題

まずは、最近傍法と呼ばれるデータの判別問題について考えてみましょう。今回は次のようなデータを考えてみます。

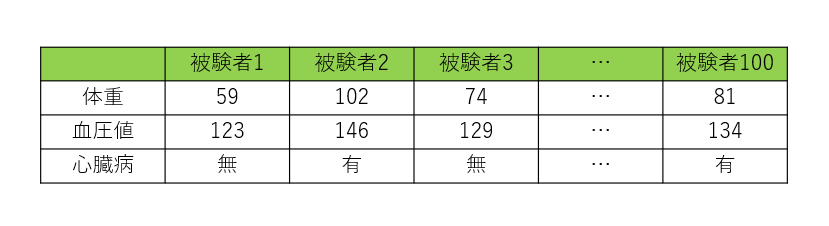
これは、言ってみれば”横長”のデータです。このデータを可視化してみましょう。実際に平面上にプロットしたものが次の図になります。

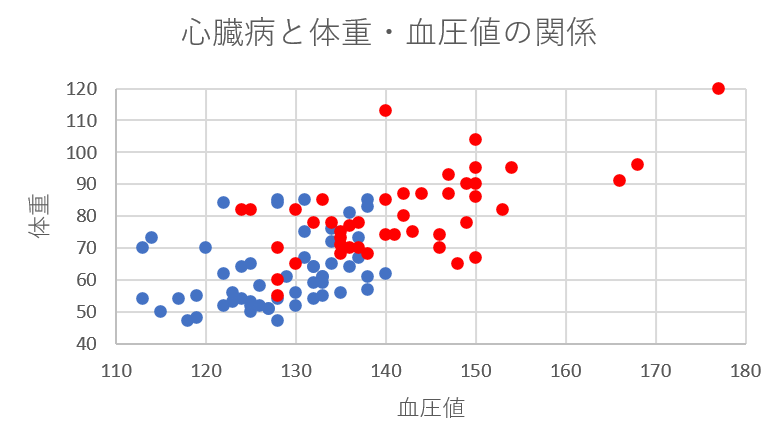
青色のデータが健康な人、赤色のデータが心臓病を患っている人のデータです。さて、ここに新たに1人、Aさんという人が検査を受けにやってきました。この方は体重が92kg、血圧の項目が127だったとしましょう。今回の問題は、この方が健康と考えられるか心臓病を患ってしまうと考えられるか、属するグループを判別するというものです。

さて、こういった場合の一つの考え方として、この人に最も近いデータの被験者と同じ診断結果にするというものがあります。これが、機械学習で使われる“最近傍法”と呼ばれる手法です。つまり、Aさんのデータを座標平面に黒い点でプロットすると以下の位置になります。

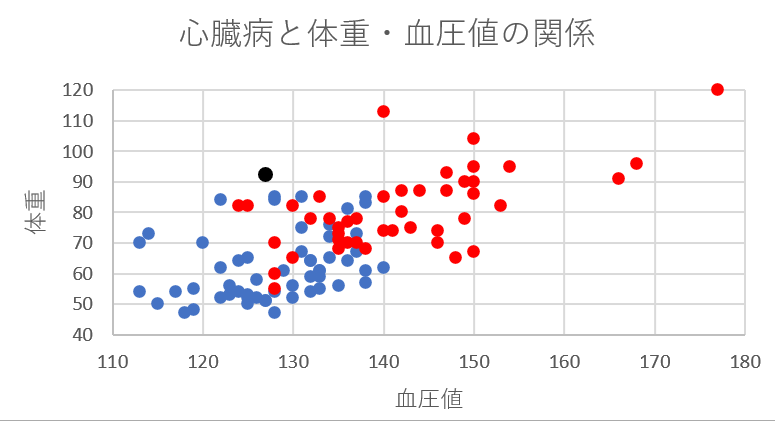
このデータでは、Aさんのデータと最も近いのは青色のデータです。ということは、Aさんは心臓病を発症しにくいグループであると判別することができるのです。最近傍法はデータの判別において有効な手法ですが、この方法を高次元データに適用しようとすると、問題が発生してしまうのです。この現象について解説していきます。

２．データの扱い

高次元データに近傍法を適用する前に、項目が複数あるデータの扱い方についてまとめておきます（前回の記事と似ているので、ご存じの方は読み飛ばしていただいても問題ありません）。

高次元データに限らず、複数の項目のデータは、次のような形（ベクトル）で表されます。

観測した項目の一つ一つを（）の中に格納しているような形です。項目が2個ある場合は2次元、10個ある場合は10次元のベクトルの形をしているという言い方になります。ここに、ベクトルの距離という考え方も導入しておきます。たとえば2次元のベクトルの場合は、ベクトルどうしの距離は次のように計算します。

要は、この値が小さければ小さいほど類似したベクトルで、大きければ大きいほどベクトルどうしが遠い、つまり似ていないということになります。2次元ベクトルの場合、これは座標平面上にプロットしたときの点と点の距離を表しています。

３．高次元データの振る舞い

それでは、先ほどの近傍法の問題に戻ってみましょう。高次元データの代表例ということで、人の遺伝子のデータを考えてみます。心臓の遺伝子の情報をデータにすることで、一人の被験者から数万という項目のデータを取得できるので、この大量の情報を医療に活かさない手はありません。先ほどと同じように100人の被験者を集め、それぞれの被験者のデータを次のように取得します。

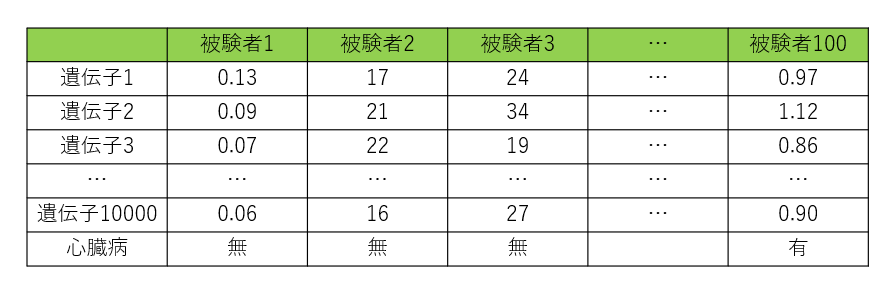
先ほど扱ったデータと違い、こちらは“縦長”のデータになります。さて、ここで新たに一人、Bさんという方の遺伝子データを取得したとします。データの距離を2章でお話した方法で計るとすると、このデータと最も近い人と同じ診断結果にすれば問題はなさそうです。しかし、実は高次元データに対しては、こういった判断をするのは望ましくないのです。というのも、Bさんに「一番近い」データというのが、距離で見ると全然近くないという現象が起こるからなんです。2次元のデータ間の距離を計算するとあまり大きな数字にはならないのですが、高次元データどうしの距離を計算すると、たいていの場合桁違いに大きな数字になっており、もはや「近い特徴」などとは言えなくなってしまうということです。

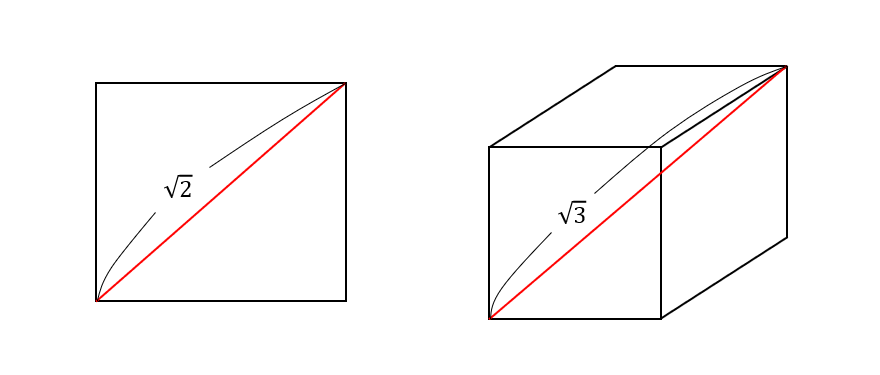
以下、この現象を図形的に見てみます。データが2次元（つまり2項目）であれば、データは平面上にプロットされます。ここで、1辺の長さが1の正方形の端から端までの長さを考えてみると、\(\sqrt{2}\)になります。つまり、1辺の長さが1の正方形の中に100個のデータをプロットする場合を考えると、端から端までの長さが\(\sqrt{2}\)の領域の中でデータが散らばることになります。

ではデータが3次元になると、今度は3次元の空間内にデータがプロットされますが、1辺の長さが1の立方体は、端から端までの長さは\(\sqrt{3}\)です。このように次元が上がれば上がるほど、データが存在する領域の端から端までの長さは大きくなっていくのです。正確には、1辺の長さが1の\(d\)次元立方体の対角線の長さは、\(\sqrt{d}\)になります。

ということは、1万次元のデータを考えてみると、その世界の立方体は端から端までの長さが100と非常に長く、この広大な世界の中に、たった100個のデータが散らばっているということなのです。つまり世界が広すぎて、一番のご近所さんまでの距離が全然近くない…という現象が起こっているということです。このような場合には、特徴が「一番似ている」はずの遺伝子の情報は、距離で見ると全然似ていないため、その被験者と同じ診断結果を下すのはあまりにも無理がある…というのが、高次元における近傍法の問題点なのでした。