↓↓↓動画で見たい方はこちら↓↓↓

みなさんこんにちは。和からの数学講師の伊藤です。前回のマスログでは、高次元データと呼ばれる現代ならではのデータをご紹介しました。そして高次元データは、従来の統計学では扱えないことが多いという点にも触れていきました。

高次元データとは？-高次元統計解析-

今回は、従来のデータと高次元データの振る舞いの違いをお話していきます。どうして従来通りの分析が通用しなかったのか、そのイメージを持っていただければと思います！

１．統計学における重要な法則

従来の統計学では、サンプルの数が大きければ大きいほど、標本平均は母集団の平均付近に集中するという大前提がよく使われていました。こういった法則のことを大数の法則と呼びます。そしてこれに関連して、標本平均の振る舞いを捉えることができる、中心極限定理と呼ばれる統計学の大定理があります。大数の法則と同じように、これも標本平均が母平均の近くで分布しているという主張になっています。こういった理論を使うことで、収集したデータの母集団の特徴を数学的に特定することが可能だったわけです。

データの次元が大きい場合もこういった方法で母集団の特徴を把握したいのですが、実は高次元データを扱う際には、こういった理論では太刀打ちができなかったのです。高次元データを扱う際にはどんな問題が起こるのか、次の章以降で見ていきましょう。

２．複数の項目があるデータの扱い方

高次元データに限らず、複数の項目のデータは、次のような形（ベクトル）で表されます。

観測した項目の一つ一つを（）の中に格納しているような形です。項目が2個ある場合は2次元、10個ある場合は10次元のベクトルの形をしているという言い方になります。この塊が1つのデータとなるので、100人のデータを得た場合はこの（）が100個できあがります。

データの標本平均や母平均も、同じくベクトルの形になります。

それから、ベクトルの距離という考え方も導入しておきましょう。たとえば2次元のベクトルの場合は、ベクトルどうしの距離は次のように計算します。

要は、この値が小さければ小さいほど類似したベクトルで、大きければ大きいほどベクトルどうしが遠い、つまり似ていないということになります。データどうしでなくても、標本平均と母平均の距離も考えることもできます。

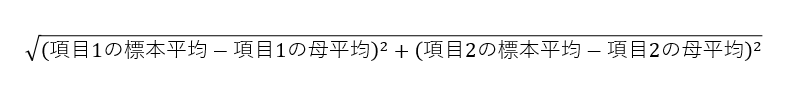
こういった道具を使って、高次元データの振る舞いを見ていきましょう。

３．高次元データの振る舞い

さて、このデータについて、例えば一番最初の観測項目だけに注目してみると、先ほどの大数の法則や中心極限定理といった理論はそのまま使えます。つまり、100人分の“観測項目1の平均値”は、“観測項目1の母集団の平均”に近い値になります。

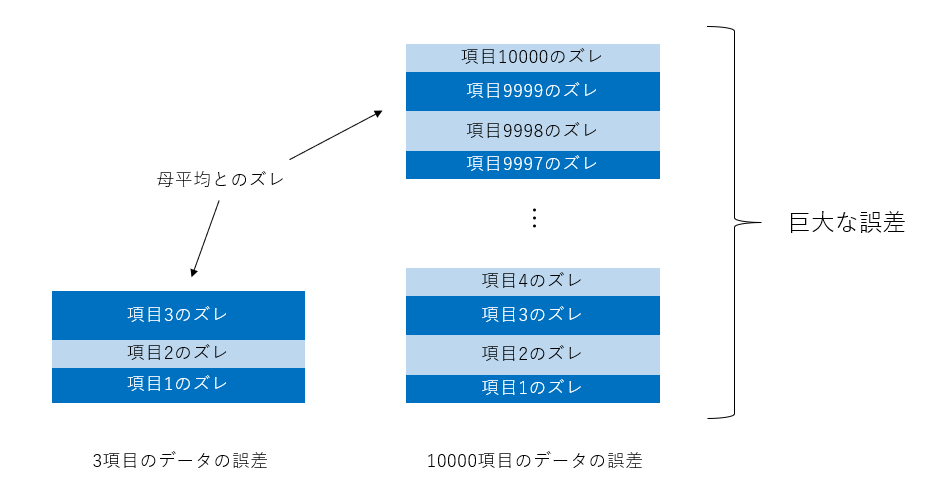
しかし高次元データにおいて問題なのは、データ全体を見てみると、全く母平均に近くない、という点にあります。どういうことかというと、標本平均ベクトルと母平均ベクトルの距離を考えてみると、項目の数が多ければ多いほど、距離が大きくなりやすいということです。つまり、1つ1つの項目は母平均付近に集中するのに、全体で見ると全く母平均に近くないという一見わけの分からない結論になってしまうのです。

しかし、これは直観的に理解することができます。というのも、確かにデータ1つ1つは母平均の近くに集中してはいますが、どれも微妙にずれているわけです。この微妙なズレが数万項目も積み重なると、データ全体で見たときには結構ずれている…という、ちりも積もれば山となる、のような現象が起こっていたのです。これが、「標本平均は母平均の近くで分布する」という統計学の前提が使えないことのイメージです。

4. 高次元データの攻略方法

ここまで、高次元データを扱う際にでてくる問題点をまとめました。では、統計学では高次元データには全く太刀打ちできないのか…というと、そんなことはありません。高次元データに対しても、新たな分析手法が提案されてきているのです。

そのうちの一つが、この「標本平均が母平均から離れる」という現象を利用してしまおうという逆転の発想です。実は高次元データを分析してみると、完全に不規則に母平均の遠くに分布するのではなく、一定の半径をもつ球面上に分布していることが見えてくるのです。この球面の半径にあたる部分を詳しく解析することで、データの振る舞いをうまく特定することができるのです。

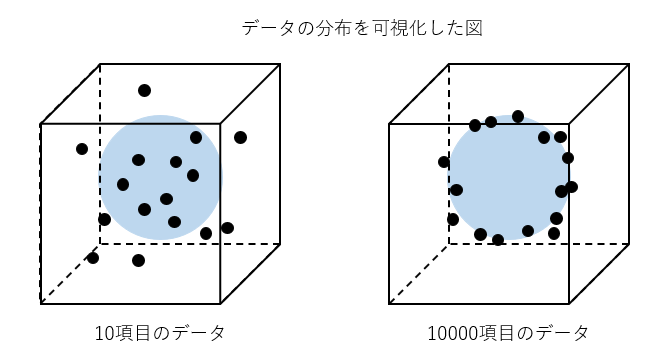
データが球面上に分布する現象は「球面集中現象」と呼ばれ、扱いが非常に厄介だと言われていたのですが、球の形をしていることを利用するという発想が、高次元データを扱う際の鍵になってきます。

5．まとめ

いかがでしたでしょうか。従来の統計学の限界と、高次元データの独特な振る舞いについて解説してきました。高次元データならではの振る舞い（次元の呪い）は他にもたくさんあるので、ぜひ統計学を勉強する際には、「次元が高くなるとどうなるかな？」と考えてみてください。思わぬところで、分析上の問題点が浮かび上がってくるかもしれません！

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/伊藤智也>

Introduction to High-Dimensional Statistics　Christophe Giraud(著)　Chapman and Hall/CRC