こんにちは。和からの数学講師の岡本です。今日は初等幾何の有名（マニアック）な話題である「モーリーの奇跡」について語っていきたいと思います。

１．フランク・モーリーの発見

古代ギリシャの時代から数多くの幾何学の問題が考察され、解決されてきました。特に三角形の合同や相似、角度や長さを使って証明されるものは「初等幾何学」と呼ばれています（注：「初等」とは「簡単」であるという意味ではありません。「初等的」とは、簡単にいうと「高度な道具を使わない」というだけのニュアンスなので、超難しい初等幾何学の問題も多く知られています。）難しい問題があるといっても、初等幾何学の問題は解決されつくされたように思われていました。
しかし、なんと1899年につぎのような定理がアメリカの数学者フランク・モーリーによって証明されました。

言葉だとわかりづらいので図で考えてみましょう。

２．定理の内容をイメージしてみる

まず適当な三角形ABCを用意します。テキトーです。

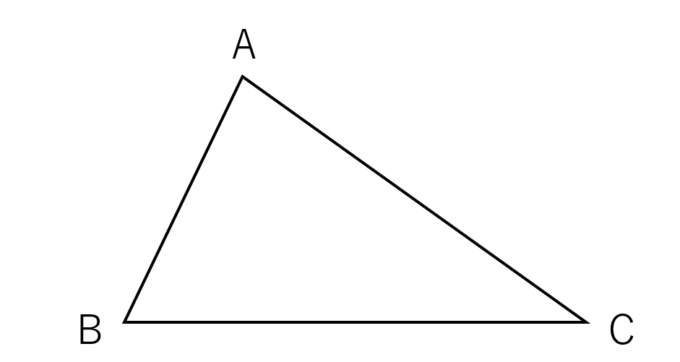
そして、各頂点から角の3等分線を引きます。

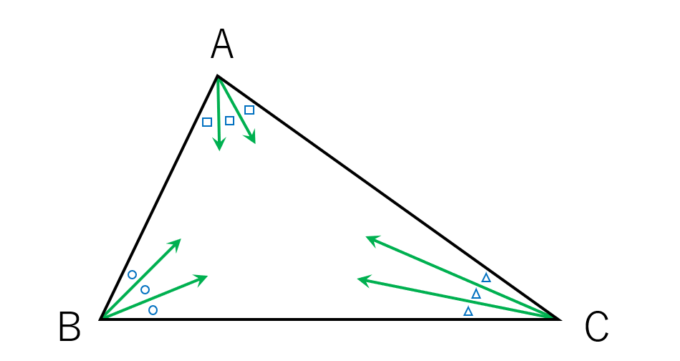
すると、隣り合う3等分線の交点ができるはずです。

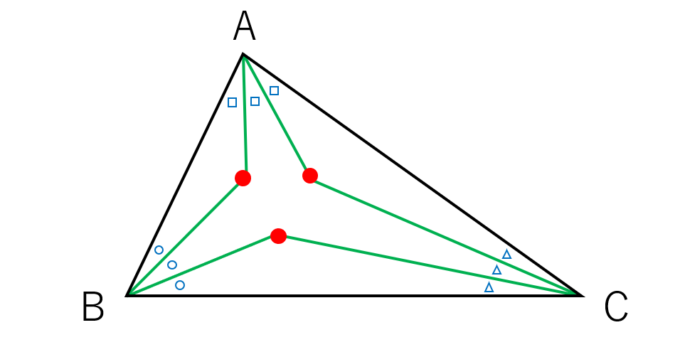
この交点を結んでみます。

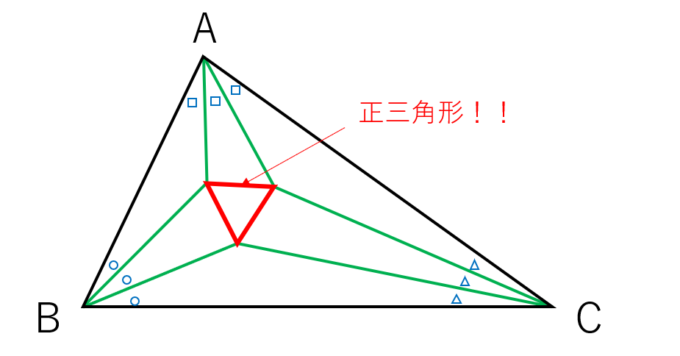
何やら綺麗な三角形ですね。そうです。これは必ず正三角形になるのです！！
えー！！！！！！！！そんなバカな！！！と思いませんでしたか？僕は最初にこの定理を見たときに思いました。

３．モーリーの奇跡

他の三角形でも試してみましょう。例えば以下のような三角形でやっています。

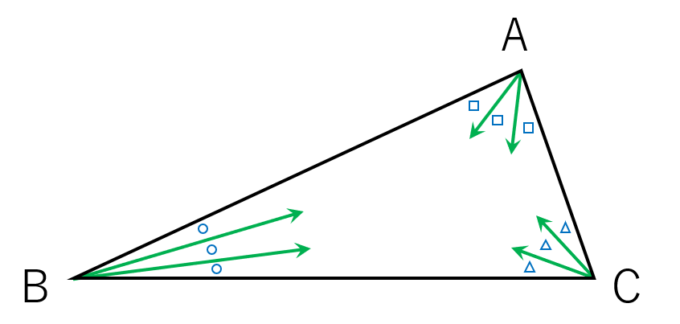
三等分して、

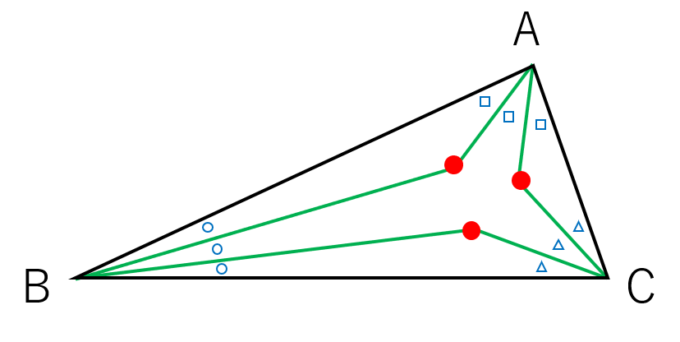
交点を結ぶと

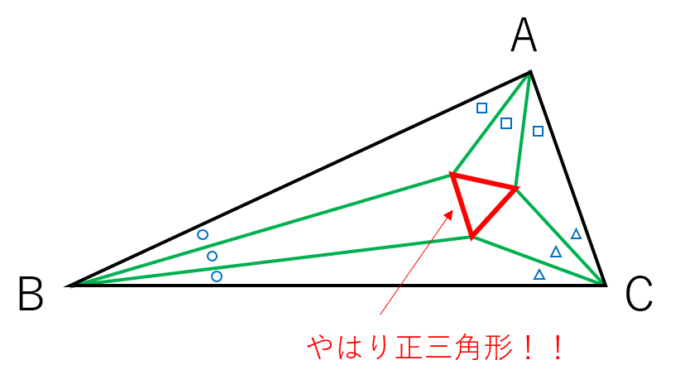
やはりそれらしい三角形が現れます！
何かすごいかって、こんなシンプルな結論が、古代ギリシャの時代から1899年までの間に誰一人として発見＋証明をされずに残っていたことです！このことから、この定理は「モーリーの奇跡」とも呼ばれています。

４．さいごに

モーリーの定理の証明はいろいろ知られていますが、意外と一筋縄にはいきません。次回、三角比を使った証明を載せてみようと思います。お楽しみに！

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングをご利用ください。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>