↓↓↓動画で見たい方はこちら↓↓↓

相関分析と回帰分析

2変数データの関係の分析の準備として初めに2変数データの定義について確認します。まず、クラス全員の得点のデータや体重のデータ、身長のデータはそれぞれ1変数データです。1変数データの分析では、平均値・中央値・最頻値や標準偏差・変動係数などを求めて分析することが多いです。
対して、2変数データは体重と身長の組のデータや気温と湿度の組のデータなどを指します。具体的に、30人のクラスにいる生徒の一人一人の身長と体重を集計すると、\(30×2=60\)個のデータが得られます。
得点のみ、身長のみのデータを考える1変数データに対して、身長と体重・気温と湿度といった２つの組のデータを集計しているため、これらは2変数データと呼ばれます。

一般的に、2変数データの関係を分析する方法として相関分析と回帰分析が存在します。この記事では、相関分析で用いる共分散と相関係数について解説します。
相関分析では、2つのデータの相関関係を評価します。対し、回帰分析では将来の値を予測することを目的にしています。相関関係とは、２つの種類のデータの関係性のことです。相関関係は片方のデータの変化に対してもう片方のデータがどのように変化するかを評価します。

共分散とは

2つの変数の関係を数値化するために、共分散が計算されます。
1変数データで用いた分散の計算では、それぞれのデータの平均からの距離（\(x_i – \bar x\)）を用いてデータの散らばりを数値化しました。2変数データの関係を調べるときは、この偏差の積を用います。
\((x_i – \bar x)(y_i – \bar y)\)
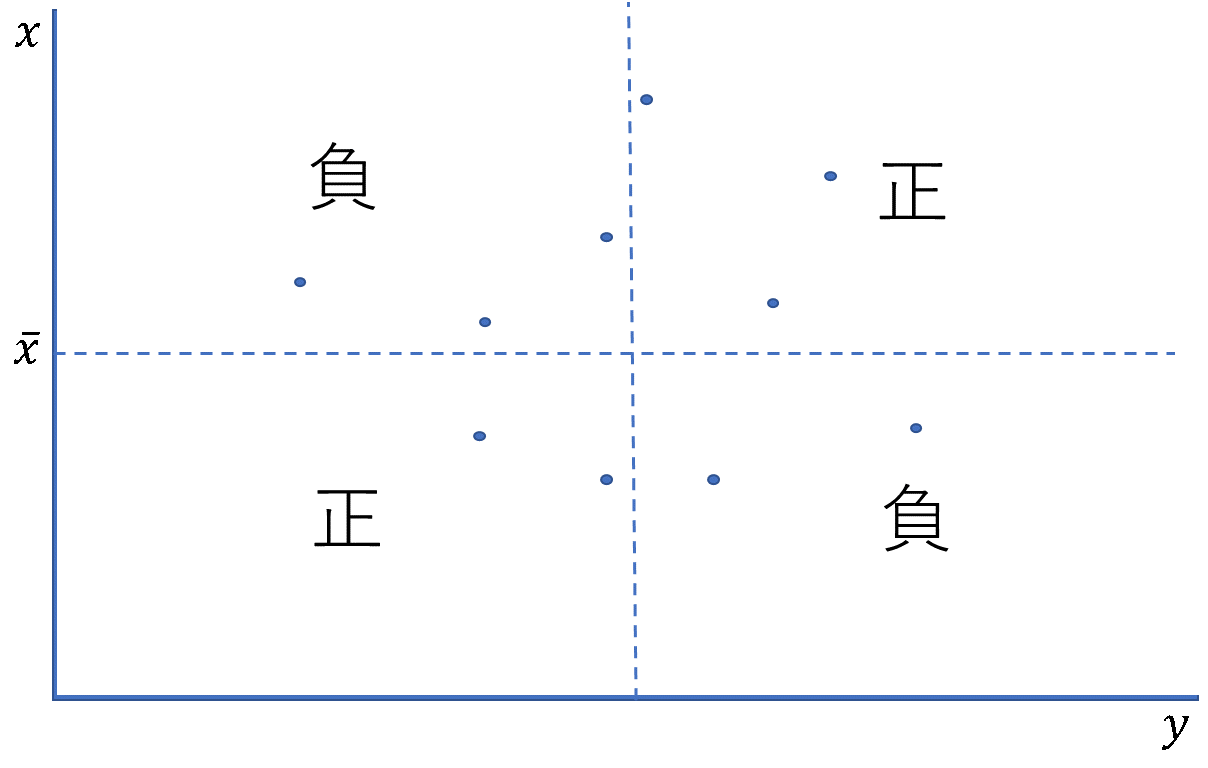
偏差の積は、\(i\)番目の\(x\)と\(y\)両方が平均を上回る/下回るとき正になります。
反対に、\(i\)番目の\(x\)が平均を上回る/下回るものの、\(y\)が平均を下回る/上回るとき負になります。

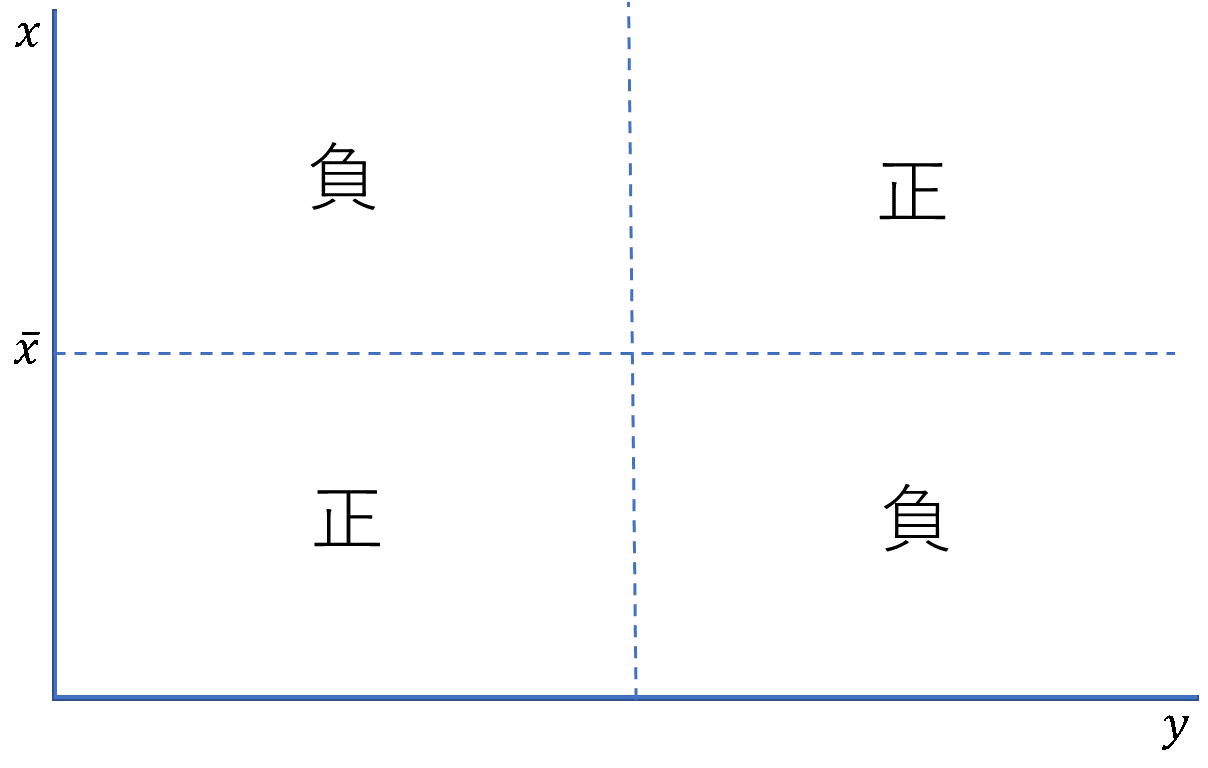
偏差の積の平均を取ることで、データの相関関係が分かります。偏差の積の平均を共分散と呼び、共分散の正負を用いて相関関係を解釈します。
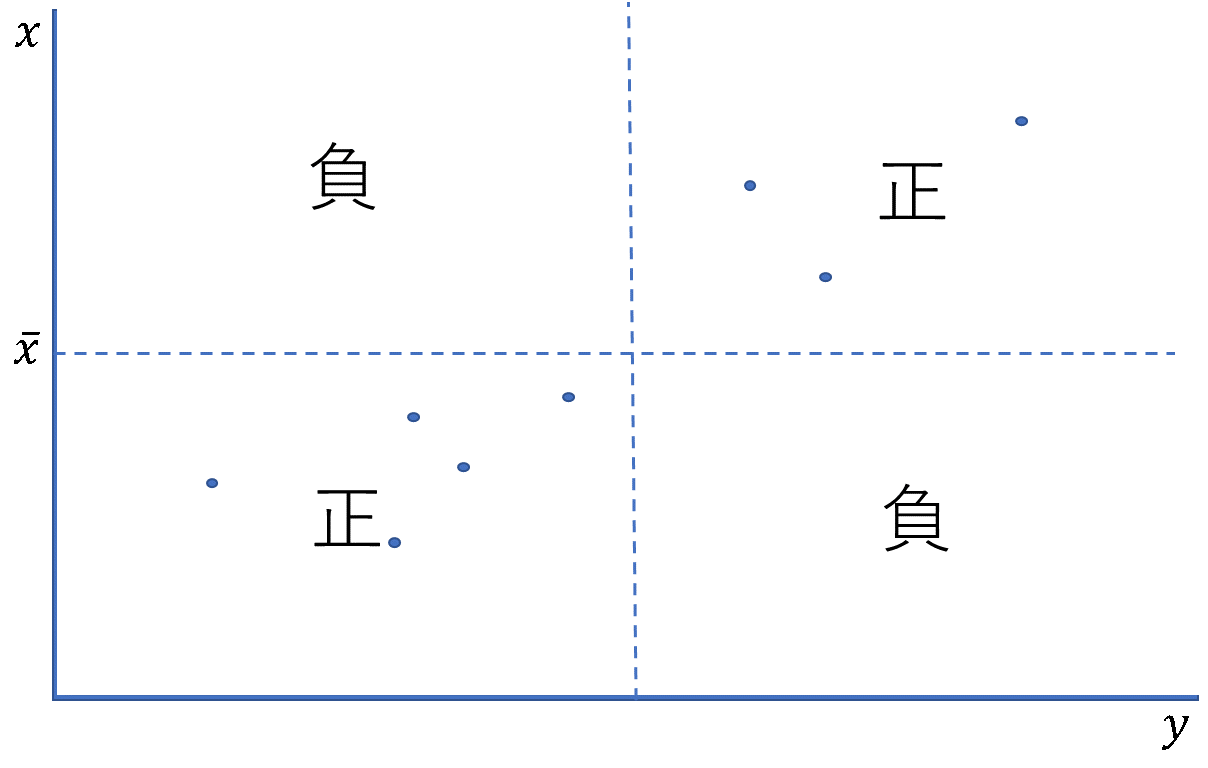
共分散が正であるとき、多くのデータについて偏差の積が正となります。\(x\)が上昇すれば\(y\)が上昇する関係が見て取れるため、正の相関があるといいます。

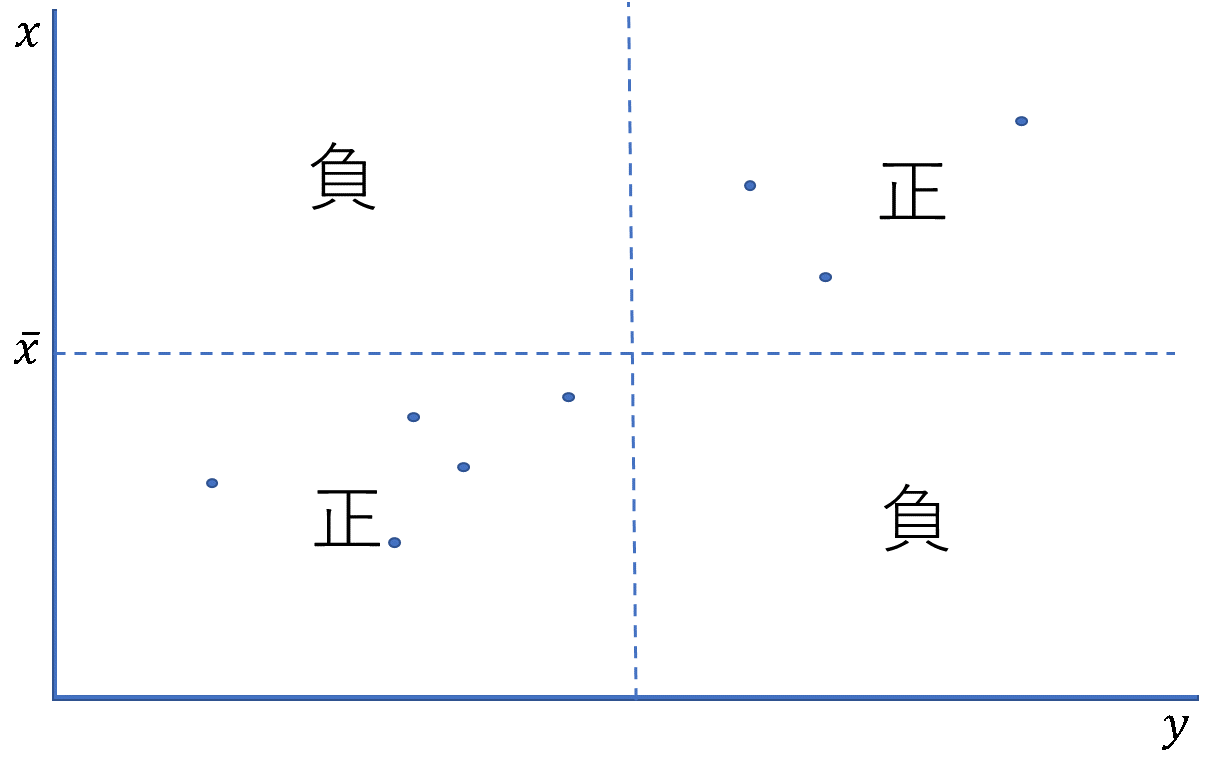
反対に、ほとんどのデータについて偏差の積が負のとき、共分散はそれらの平均であるため同じく負になります。このとき、片方が上昇するともう片方が下降する関係にあり、負の相関があるといいます。

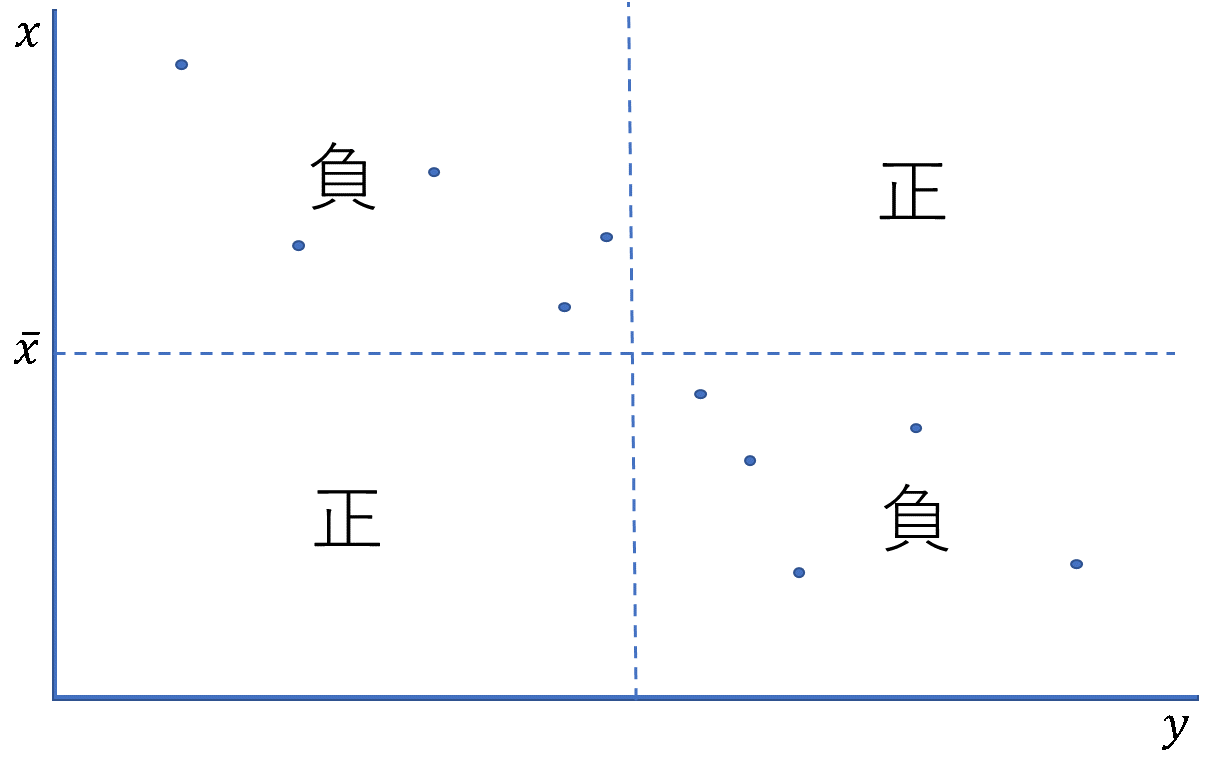
最後に、偏差の積が正のものと負のデータが同じくらいあり、平均してほとんど\(0\)であるとき共分散は\(0\)に近くなります。このとき、データは無相関であるといいます。

相関係数とは

前のセクションでは共分散を用いて正・負の相関や無相関が判別できると説明しました。しかし、共分散のみでは相関関係を比較することが難しいです。
例えば、身長と給与に関して共分散を計算するとき、給与は何百万といった単位であるため共分散は必然的に大きい値になりやすくなります。
データの種類や性質によって共分散の大きさが変わってしまうため、客観的に相関関係を評価したい場合や比較を行いたい場合は相関係数が用いられます。

相関係数は共分散を\(x\)と\(y\)の標準偏差で割ることによって計算されます。相関係数は共分散と同様に正であれば正の相関、負であれば負の相関、\(0\)に近ければ無相関を表します。
また、相関係数は必ず\(-1\)から\(1\)の間に収まるという性質を持っています。そのため、\(1\)に近ければ近いほど正の相関が強く\(-1\)に近ければ近いほど負の相関が強いと判断できます。
実際に、相関係数が\(1\)、\(-1\)である場合にはデータが一直線に並ぶことが知られています。

まとめ

この記事で解説した共分散と相関係数は2変数データの代表的な分析方法である回帰分析に用いられる計算にも用いられます。相関分析では、2つのデータの相関関係を評価します。対して、回帰分析は過去のデータに基づいて予測することを目的にしています。また、回帰分析を因果推論に応用することも可能です。因果関係は片方が原因となってもう片方の変数に影響を与えるという関係です。このような因果関係の有無を推定する学問を因果推論と呼び、経済学で近年トレンドとなっている学問分野です。　

●お問い合わせフォームはこちら

<文/須藤>