↓↓↓動画で見たい方はこちら↓↓↓

最頻値とは

最頻値とは、データの中で最も頻繁に現れる数です。例えば、度数分布表であれば最頻値は度数が最も大きい階級になります。また、サイコロを振って\(6\)の目が\(3\)回、\(5\)の目が\(2\)回、\(1\)の目が\(1\)回出たとすると、最頻値は\(3\)回現れた\(6\)です。
最頻値はデータの代表値の一つです。沢山あるデータを端的に表すことができるのが代表値の特徴で、他には平均値や中央値が有名です。最頻値は最も多く現れた数を提示するため、そのデータの中で出やすい値が何かが分かります。
以下では、最頻値の求め方とその解釈の方法を解説します。

最頻値の求め方

最頻値の求め方のポイントは一度データを並び替えてから重複する数を数えるということです。具体的には、データを小さい数から大きい数に並び替えると良いでしょう。
例えば、
\(1,2,4,5,4,2,3,4,1,6,4,7,3,2,7\)
というデータを考えてみましょう。このデータを小さい方から並び替えると、
\(1,1,2,2,2,3,3,4,4,4,4,5,6,7,7\)
このように並び替えると\(1\)が\(2\)個、\(2\)が\(3\)個、\(3\)が\(2\)個、\(4\)が\(4\)個、\(5\)が\(1\)個、\(6\)が\(1\)個、\(7\)が\(2\)個あると分かります。重複する数が一番多いのは\(4\)なので、\(4\)が最頻値と分かります。
また、
\(1,3,4,1,6,4,7,3,2,7\)
というデータを並び替えると
\(1,1,2,3,3,4,4,6,7,7\)
となります。この場合\(1,3,4,7\)がそれぞれ\(2\)つずつあり、最も多いので最頻値は一つには定まりません。そのため、最頻値は\(1,3,4,7\)と求められます。
最後に、
\(1,2,3\)
というデータの最頻値を考えてみましょう。この場合重複して出現する数はないため、最頻値は全ての数（\(1,2,3\)）になります。

最頻値の考え方

最頻値の求め方が分かったところで、最頻値の使い方や解釈について考えてみましょう。最頻値は平均値や中央値と同じように、データの特性を見るために使われます。下のような分布のデータがあったとき、中央値と平均値は最頻値の右に位置します。このように最頻値・中央値・平均値はデータの代表値であるものの、値が大きく異なることがあります。

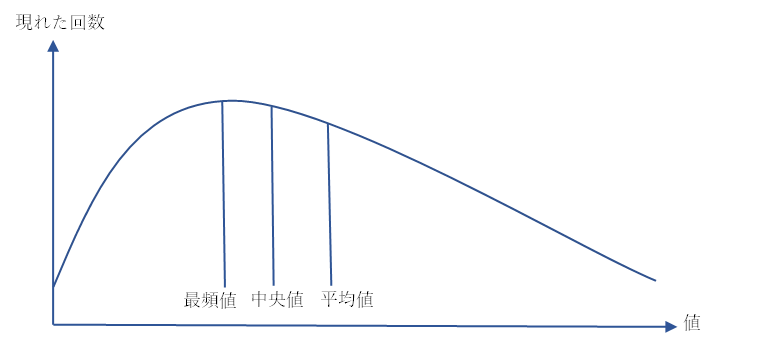
また、下のような分布を見てみると、出現数が多い部分が2つあることに気づきます。値が小さい所と値が大きい所に\(2\)つ山があるため、中央値・平均値はその間にあります。

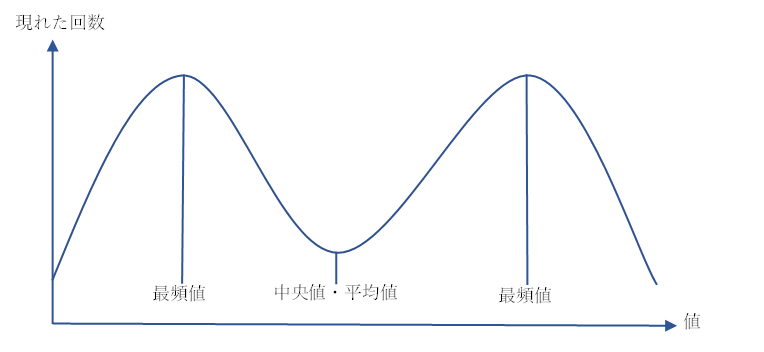
最頻値を用いることで、どの部分のデータが多く存在しているかが分かります。また、中央値や平均値と合わせて最頻値をみることによって、データの分布についてイメージすることができます。

まとめ

この記事では、最頻値の計算方法とその考え方を紹介しました。例を挙げると、最頻値を求めることでアンケート結果の集計であれば回答者の多数の意見を把握することができます。
また、統計分析で用いられることの多い代表値として、最頻値の他に平均値と中央値があります。ぜひこの機会にこれらの代表値の性質や求め方も確認してデータを見る力を鍛えましょう。

●お問い合わせフォームはこちら

<文/須藤>