↓↓↓動画で見たい方はこちら↓↓↓

度数分布表とは

度数分布表とは、データを複数の区間に分割して、それぞれの区間にいくつデータが存在するかを調べ上げた表です。分割したそれぞれの区間のことを階級と呼び、そこに属するデータの数を度数と呼びます。\(0\)以上\(10\)未満、\(10\)以上\(20\)未満、\(20\)以上\(30\)未満、\(30\)以上\(40\)未満の階級を持つ度数分布表を考えましょう。各階級の一番大きい数字と小さい数字の差はそれぞれ\(10\)（\(=20-10\), \(=30-20\),…）なので、階級の幅が\(10\)であると言います。階級の幅が階級ごとに異なると各階級に対して度数の大小が分からなくなってしまうため、階級の幅は通常一定です。最後に、階級の階級値は階級の真ん中の値となります。同じ例を用いると、それぞれ\(5\)、\(15\)、\(25\)、\(35\)です。このように、度数分布表は階級と度数が対応しており、階級の性質を把握するため階級値や階級の幅を参照します。

度数分布表の見方

下のグラフは\(25\)人の生徒が\(100\)点満点のテストを受けた際の度数分布表です。

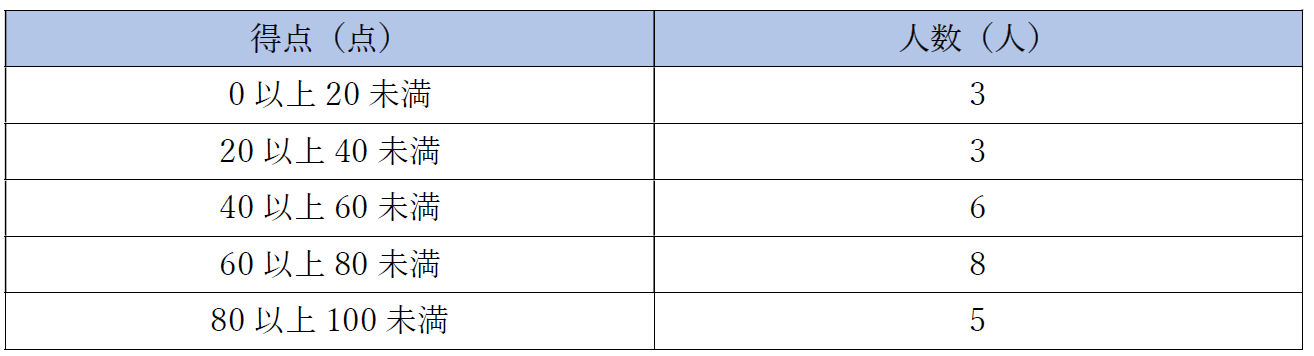
得点が\(5\)つの区間に分けられているので、階級は左側の列にある\(0\)以上\(20\)未満、\(20\)以上\(40\)未満、…の欄に対応すると分かります。また、階級ごとのデータの数は人数で表されるため度数は右側の列にある\(3\)、\(3\)、\(5\)、…の欄に対応すると分かります。階級の幅はそれぞれの階級に着目して、\(20-0=20\)、\(100-80=20\)などと求められます。最後に、階級値は中央の値を選択すればよいので、上から順に\(10\)、\(30\)、\(50\)、\(70\)、\(90\)となります。

これらの基本的な情報を抑えたうえで、次に度数分布表からデータの特性について考えます。\(60\)以上\(80\)未満の階級は最も度数が高く、続いて\(40\)以上\(60\)未満、\(80\)以上\(100\)未満の階級となっています。また、\(0\)以上\(20\)未満、\(20\)以上\(40\)未満の階級は他の階級と比べて度数が低いため、得点が低かった人が多くないことが分かります。
加えて、度数分布表を見ることによって中央値がどの階級に属するかを確認することができます。\(25\)人の得点を低い順に並べたとき、中央値となるのは\(13\)番目の生徒の点数です。そのため、度数分布表の度数を下の階級から順に足し合わせることで中央値の階級が分かります。\(0\)以上\(20\)未満、\(20\)以上\(40\)未満はそれぞれ度数が\(3\)なので、\(40\)点以下を取った生徒は\(6\)人です。次に、\(40\)以上\(60\)未満の階級の度数は\(6\)なので、\(60\)点以下の点数の生徒は\(12\)人です。次に高い点数の生徒は次の階級である\(60\)以上\(80\)未満に属しているため、\(13\)番目に低い点数＝中央値の階級が分かりました。
中央値と違い、平均値の階級は計算によって求められるケースがあれば求められないケースもあります。そのため、度数分布表から平均値を概算するための方法があります。度数分布表のデータだけではそれぞれのデータの正確な値が分からないため、近似的に属する階級の階級値をデータの値だとします。上の度数分布表の例の場合、\(10\)点の生徒が\(3\)人、\(30\)点の生徒が\(3\)人、\(50\)点の生徒が\(6\)人、\(70\)点の生徒が\(8\)人、\(90\)点の生徒が\(5\)人いると考えることができるため、
平均値　\(≒10×3+30×3+50×6+70×8+90×5=57.2\)
となります。

度数分布表の活用

度数分布表を利用することで、データを簡単にまとめることができます。\(25\)人のテストの個別の得点を眺めているだけでは高得点層の人数が多いことや中央値が\(60\)以上\(80\)未満点の階級に属することは分かりません。反対に、前述したように中央値や平均値の具体的な値を度数分布表から計算することはできないためデメリットも存在します。
また、度数分布表を作成することで、度数分布表を視覚的に見やすい形で表現するヒストグラムや他のデータとの比較の際に有用な度数分布多角形を作成することができます。このように、表やグラフを用いてデータを要約する手段を習得していきましょう。

●お問い合わせフォームはこちら

<文/須藤>