ハッピーな数?―数たちの知られざる性質―
公開日
2020年7月14日
更新日
2020年7月14日

こんにちは。和からの数学講師の岡本です。みなさんは数を見て「ハッピーだ!」なんて感じることありますか?僕はあります。例えば、不意に目に入った数が素数だったらなんだかうれしいです
その他にも、ロマンティック数学ナイトのプレゼン時間でおなじみの「完全数」。(完全数とは、その数以外の約数を全て足し和わせると元の数に一致するような特殊な数です。弊社で開催している数学のプレゼン交流会「ロマンティック数学ナイト」の一人当たりのプレゼン時間は3番目の完全数である496秒を採用しています。)
このような「特別な性質」を持った数には特別な感情を抱きます。今日ご紹介するのは、「ハッピー数」と言われる数についてです。名前からしてハッピーですね!一体どんな数なのでしょうか!
この記事の主な内容
1.ある操作
まず、皆さんになんでもいいので数を一つ選んでもらいます。例えば\(57\)など、なんでも構いません。次に選んだ数の各桁の数を全て2乗してあげます。\(57\)を選んだ場合、\(5\)と\(7\)をそれぞれ2乗して\(25\)と\(49\)を値作り出します。その後、それらの数を足し合わせます。\(57\)を選んだ場合、\(25+49=84\)となります。この操作で数\(57\)は、新しく\(84\)へと移り変わりました。以下、この操作のことを「\(F_2\)」と書くことにします。
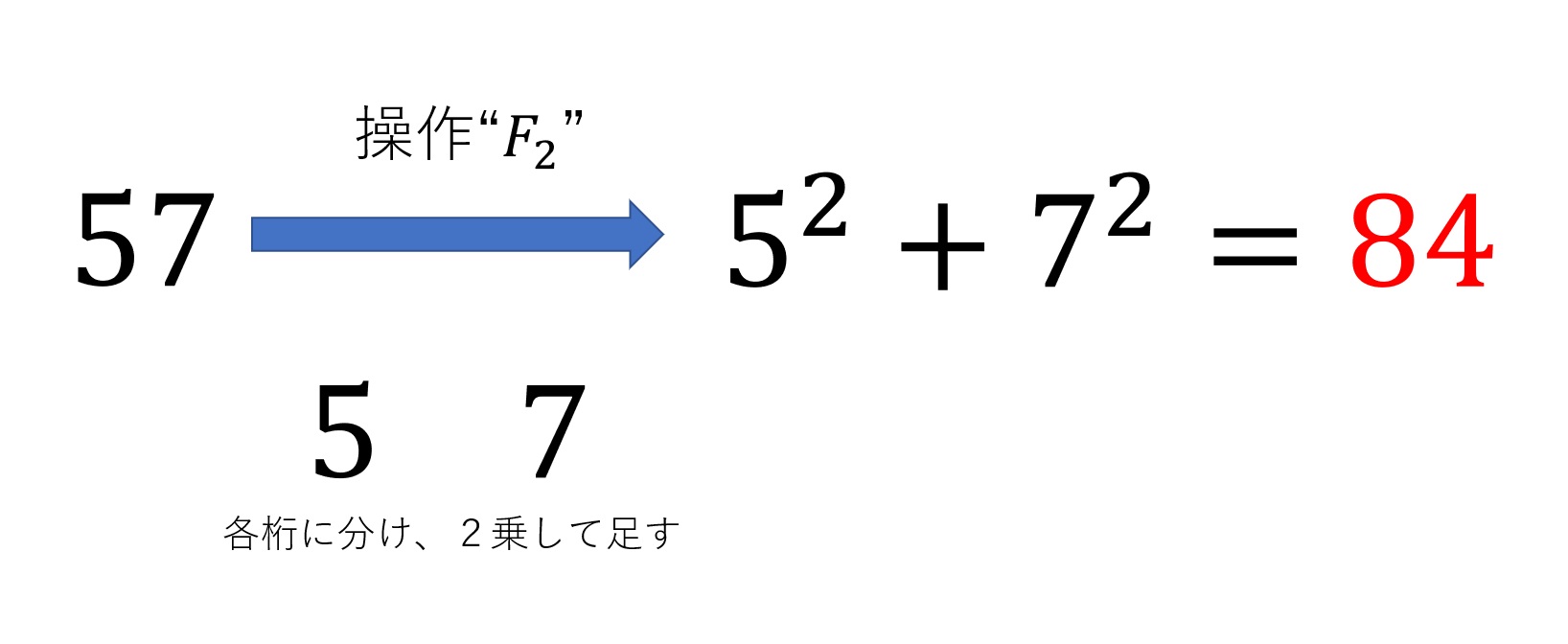
続いて今の操作\(F_2\)をもう一度繰り返します。つまり、\(84\)に対してもう一度同じ計算を行います。\(8\)と\(4\)の2乗の和は\(64+16=80\)となり、\(84\)は\(80\)へと移ります。
みなさんはこの操作\(F_2\)をずーーーっと繰り返してみてください。初めに\(57\)を選んだので、このまま続けていきます。

2.行き着く先は?
いかがでしたか。ずーっと続けると「あるパターン」に陥ると思います。\(57\)を選んだ場合、操作\(F_2\)を続けると\(4\)に移りました。その後操作を続けると\(16\), \(37\), \(58\), \(89\),…となり、途中に現れた、\(89\)に戻ってきました。つまり、「無限ループ」に陥ってしまったのです。

もしかするとこの操作を行って\(1\)になった方もいらっしゃるかもしれません。例えば\(23\)を選ぶと、\(4+9=13\), \(1+9=10\), \(1+0=1\)となり、1度\(1\)に到達してしまうとそこから動きません!つまり、「ゴール」にたどり着いたのです。

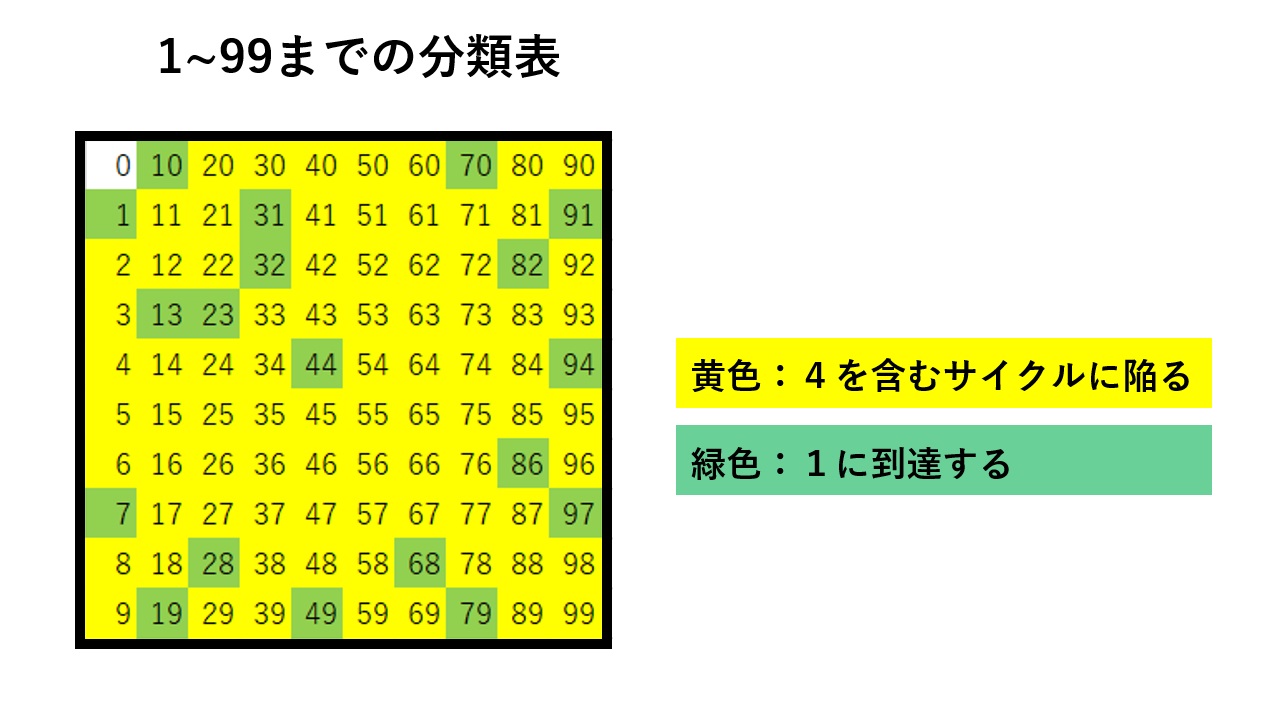
実はどんな数でも、「各桁を2乗して足す」という操作を繰り返していくことで、「4を含むサイクル」に陥るか、「1」に到達するかの2通りしかないことが知られています!
何度か操作\(F_2\)を施して「1」というゴールにたどりつく数のことを「ハッピー数」といいます!実際、ほとんどの数が「4を含むサイクル」に陥てしまうので、ある意味「1」にたどり着く数は“貴重”なのです。こういった意味で「ハッピー数」と名前が付けられています。
3.2通りしかないことの証明
前節では「4を含むサイクル」に陥るか、「1」に到達するかの2通りしかないという驚くべき結論をご紹介しましたが、やはりなぜなのか気になりますよね。ここで簡潔にその証明をしていこうと思います。
まず、10進法で\(n\)桁の数を\(A=a_1a_2\cdots a_n\)と表します。このとき\(A\)に操作\(F_2\)を施すと
\begin{align*}A \longrightarrow a_1^2+a_2^2+\cdots+a_n^2=A’\end{align*}
となります。ここで、各桁の数は0~9までの数であることに注意すると、\(A’\)は
\begin{align*}A’\leq 9^2+9^2+\cdots+9^2=81n\end{align*}
となります。例えば、10桁の数\(X\)があったとしましょう。すると、どんなに\(X\)が大きくても、操作\(F_2\)を施すと高々\( 81 \times 10=810\)(少なくとも3桁以下の数)にしかならないことがわかります。
つまり、ある程度桁数が大きい数は、基本的に操作\(F_2\)を施すと、元の数よりも大幅に小さなな数になることがわかります!
しかし、\(89\)のように、ある程度小さい桁の数は操作\(F_2\)により、\(8^2+9^2=145\)と、元の数よりも大きくなることがあります。つねに元の数よりも小さくなる桁の境目がどこなのかを求めるには対数を使って計算することができます。対数に関しては以前のマスログ記事(海難から人々の命を救う数学-対数の発見-)に詳しい解説が載っていますので合わせてご覧ください!
さて、「ある程度大きい桁」とはどれぐらいなのか、対数を使った不等式を考えます。つまり
\begin{align*}n \geq \log_{10}(81n)\Leftrightarrow n\geq 4\log_{10}3+\log_{10}n=1.9084\cdots +\log_{10}n\end{align*}
を満たす最小の\(n\)を探せばOKです。普通に不等式で解けないので、\(n\)に値を代入していきます。\(n=3\)のとき
\begin{align*}3\geq 1.9084\cdots +\log_{10}3=1.9084\cdots +0.4771\cdots\end{align*}
より、不等式が成り立ちます。つまり、3桁の数は、操作\(F_2\)により、必ず2桁以下に数になることがわかりました。しかし\(n=2\)の場合、
\begin{align*}2<1.9084\cdots +\log_{10}2=1.9084\cdots +0.3010\cdots\end{align*}
となるので、2桁の数は操作\(F_2\)によって必ずしも桁が下がらないことがわかります。
ここまでの議論としてわかったことをまとめると、「3桁以上の数は、操作\(F_2\)を何度か繰り返すといつか2桁の数まで落ちてくる」ということがわかったのです!つまり、あとは2桁の数をしらみつぶしに見ていけばいいのです!無限にある数の分類が、1~99までの数についての考察で済んでしまう。。。数学の偉大さを感じます!
なお、Excelを使って2桁の数を入れると操作\(F_2\)を行ってくれる関数を作り、実際に1~99までの数について、「4を含むサイクル」パターンか「1」到達パターンか調べてみました。

実際にこの2パターンしかないことがわかります。以上で、任意の数に対して証明が終了しました。
4.一般化の妖精
数学好きな人は「一般化」を考えたくなってしまいます。僕も一般化を考えたくて仕方ありません。「2乗じゃなくて、3乗だったらどうだろう?」こう耳元で”一般化妖精さん”がささやきます。
たしかに3乗だとどうなるのか考えてみたくなりますね。たとえば、\(25\)という数に対して、各桁を3乗する操作\(F_3\)を考えます。すると\(2^3+5^3=8+125=133\)となります。この操作\(F_3\)は実は一気に複雑になります。2乗の場合、「4を含むサイクル」か「1」になるかの2通りでしたが、3乗の場合、全部で9通りの結果になることが知られています。
サイクルは「919を含むサイクル」、「136を含むサイクル」、「55を含むサイクル」、「160を含むサイクル」の4種類。しかも「1」以外にも、到達パターンが「153」、「370」、「371」、「407」と5種類現れます。例えば「153」に対して、操作\(F_3\)を行うと

非常に不思議ですよね。実は一般に\(n\)乗する場合、サイクルがいくつで、到達パターンがいくつになるか全くわかっていないのです…!
さらに“一般化妖精さん”は負い打ちを書けるようにこう言います。「10進法にこだわらなくてもいいよね?」
たしかに…!「各桁の数を~」って言っている時点で10進数表示を仮定していました。。。これは一般に「N進数表示の数の各桁」の数を何乗かして、足し上げ、N進数表示にする。。。完全に死角でした。
そして“一般化妖精さん”はこうも言います。「2乗する、3乗するだけじゃなくて、一般に整数から整数への写像を考えてもいいよね?」
あああああ。。。とんでもなく一般化されてしまった!!!たしかに「2乗する」という操作は「整数から整数へ移す」操作の特殊な場合です!!このように数学というのは、いくらでも「一般化」することができます。ただし、むやみに一般化するのもあまり良くありません。通常では、一つの体系として統一的に整理できるような「うまい一般化」というものを見つけ出し、研究が行われます。
なお、一般化妖精さんによる一般化の結果は多分ほとんど知られていないので、みなさんぜひ解き明かしてください!
5.さいごに
いかがでしたでしょうか。比較的簡単な操作によって、数の分類ができる例として今回はハッピー数というものを紹介いたしました。そのほかにも数にはいろんな性質があります。数の性質は面白いお話についてまとめられた本として、デイヴィッド・ウェルズの「数の事典」がおすすめです。
もう少しポップな話題としては「数字マニアック」という本もあり、1~200までの数字に関するトリビアがまとまってあり、非常に面白いです。
また、今回ご紹介した数の性質や構造というものも、デザインやアートに活かすことができます。例えば、フィボナッチ数からできる模様、ユークリッドの互除法からできる模様など様々です。こうした数学を使ったアートやデザインに関する無料セミナー(オンライン)も開催していますので、ご興味のある方は是非一度お越しください!
また、岡本の数学アート作品、デザイングッズはこちらから
和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。
<文/岡本健太郎>
















