さて、前回に引き続き、「フランス式指電卓」のお話をしていきたいと思います。

フランス式指電卓ってなに？という方は前回の記事をご覧ください。

ドラマで数学！フランス式指電卓とは？≪前編≫

両手の指を使って、一桁同士の掛け算が簡単にできる指電卓。
九九を覚えている人にはあまり実用性はないかもしれませんが、今回は「なぜそんなことができるのか？」ということに焦点を当て、実際に計算が正しいことを証明していきたいと思います。

１．フランス式指電卓の証明

まず注意したいのは、このフランス式指電卓が有効なのは5より大きい数同士の一桁の掛け算です。これは、カウントを小指から折り返した後に「立っている指」の本数を見る必要があるからです。
　ではさっそく数式を使って証明してみましょう！前回は９×７を例にしましたが、今回は５より大きい２つの（一桁の）数をa, bとして、掛け算a×bを考察していきます。

まずは十の位について考えてみます。
十の位は、“立っている指”を足し算することで計算できますが、そのためにはまず“立っている指”が何本かを求める必要があります。

[左手の立っている指] ａ－５
[右手の立っている指] ｂ－５
◎十の位の数　（ａ－５）＋（ｂ－５）

次に一の位について考えてみましょう。
一の位は、“折れている指”を掛け算することで計算できます。
“折れている指”の本数を求める時は下のような式になります。

[左手の折れている指] １０－ａ
[右手の折れている指] １０－ｂ
◎一の位の数　（１０－ａ）×（１０－ｂ）

さて、ここまで来たら2桁の数にするだけですね。
例えば十の位が６、一の位が３なら　（６×１０）＋３＝６３　となりますので、同じように組み立てていきます。

｛（ａ－５）＋（ｂ－５）｝×１０＋（１０－ａ）×（１０－ｂ）

これを計算していくと、

＝１０ａ＋１０ｂ－１００＋１００－１０ａ－１０ｂ＋ａｂ
＝ａｂ

つまり「ａ×ｂ」という掛け算に収まることになるのです。

２．計算の注意点

注意点として、「一の位の数」を決める計算が10より大きくなる場合があります。たとえば「６×６」に対してフランス式指電卓の方法を使うと、立っている指の数は共に１本なので、「十の位の数」として１＋１＝２を考えます。
次に、折れている指は共に４本なので、掛け算により４×４＝１６となります。本来はこれが「一の位の数」になるはずですが、１６は１０より大きいので、１６の一の位の数６を採用し、十の位の１を先ほどの２と足し合わせることで、「３６」という数字が出来上がります。

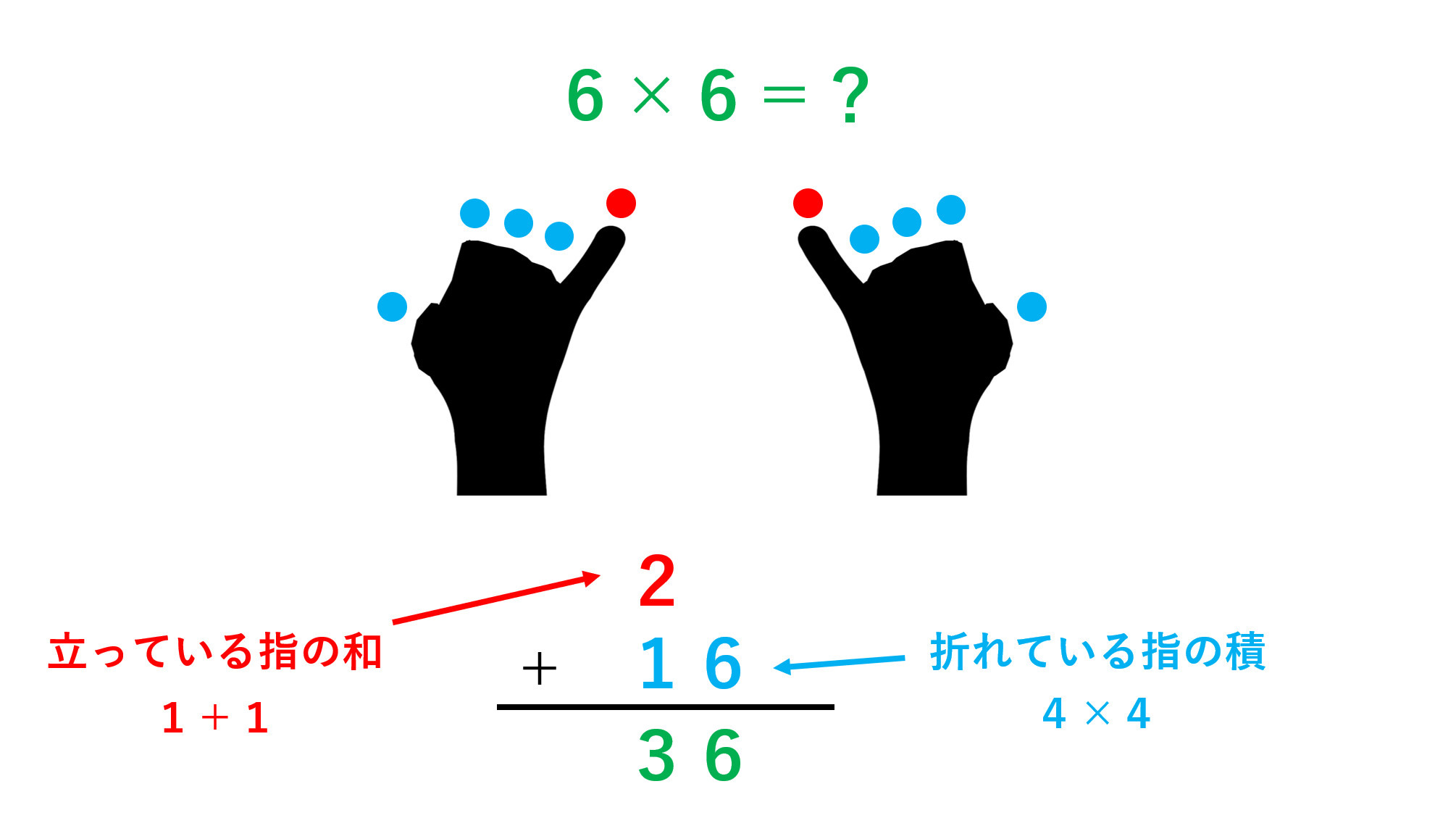
まとめると、フランス式指電卓とは、５より大きい数同士の九九の計算を、５以下同士の九九の計算で実現できるように工夫された計算方法と言えます。

３．まとめ

今回は指電卓の証明に挑戦してみましたが、いかがでしたでしょうか？

ドラマを見ていただけだったのが、思いがけず新しい発見になり、私自身楽しかったです。
（和からに入社して以来、あらゆる「数学」の話題に敏感になります笑）
みなさんにとっても新鮮な気づきになっていれば嬉しいです。

少し複雑に感じた方は、是非自分の指を使って一つ一つ確認しながら計算してみてください！

<文/池下>