必見!?ホールの結婚定理!~結婚できるとは言っていない~
公開日
2021年9月2日
更新日
2021年9月2日
こんにちは。和からの数学講師の岡本です。今回は「ホールの結婚定理」という、ものすごい名前の定理をご紹介しようと思います。この定理はグラフ理論、組み合わせ理論に関する有名な定理であり、イギリスの数学者フィリップ・ホールに由来します。グラフ理論に関する話題は以前マスログでいくつかご紹介しました。
この記事の主な内容
1.マッチング問題
次のような問題を考えてみます。
男性5人、女性5人の合計10人の集団に対して、男女のペアを5つ構成しようと思います。

また、ペアを作るときの参考として、あらかじめ女性側の要望としていくつペアとなる相手の候補を聞いておきました。
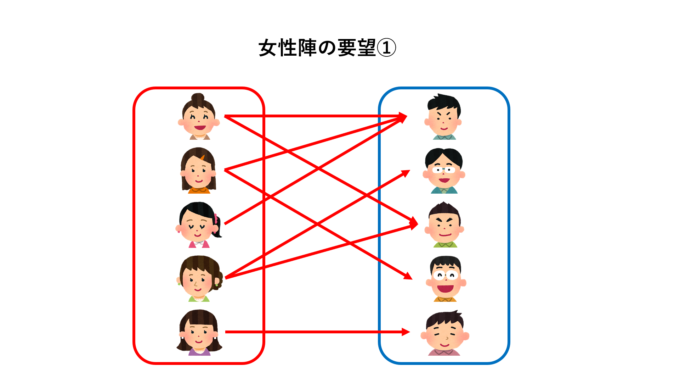
上のような要望①の場合、例えば次のような緑の矢印でペアを決められます。
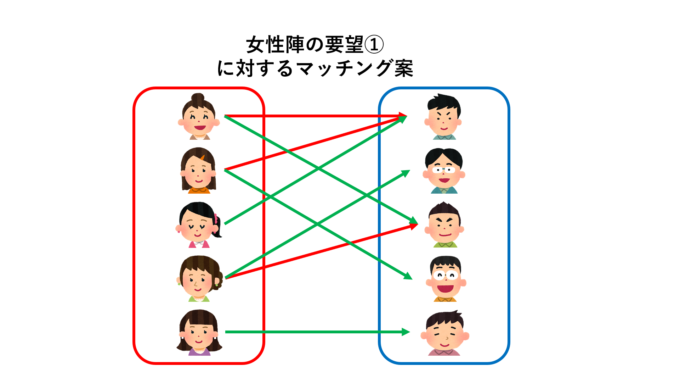
では、次の要望②に応えられるようなペア(マッチング)は組めるでしょうか?
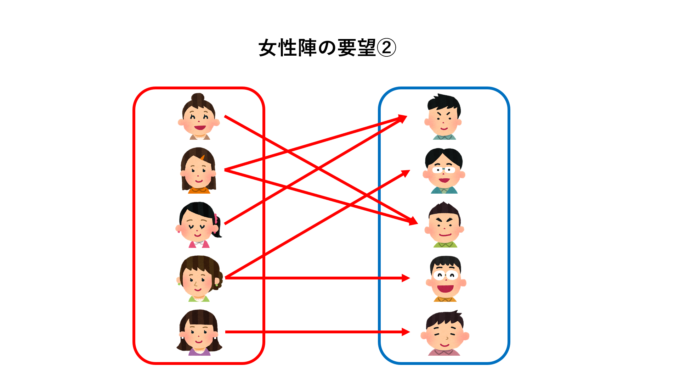
ここで重要なのは、「どう組み合わせるか」ではなくて「要望に応えられるかどうか」に対するYESかNOの2択問題であるという点です。
2.グラフを使って整理してみる
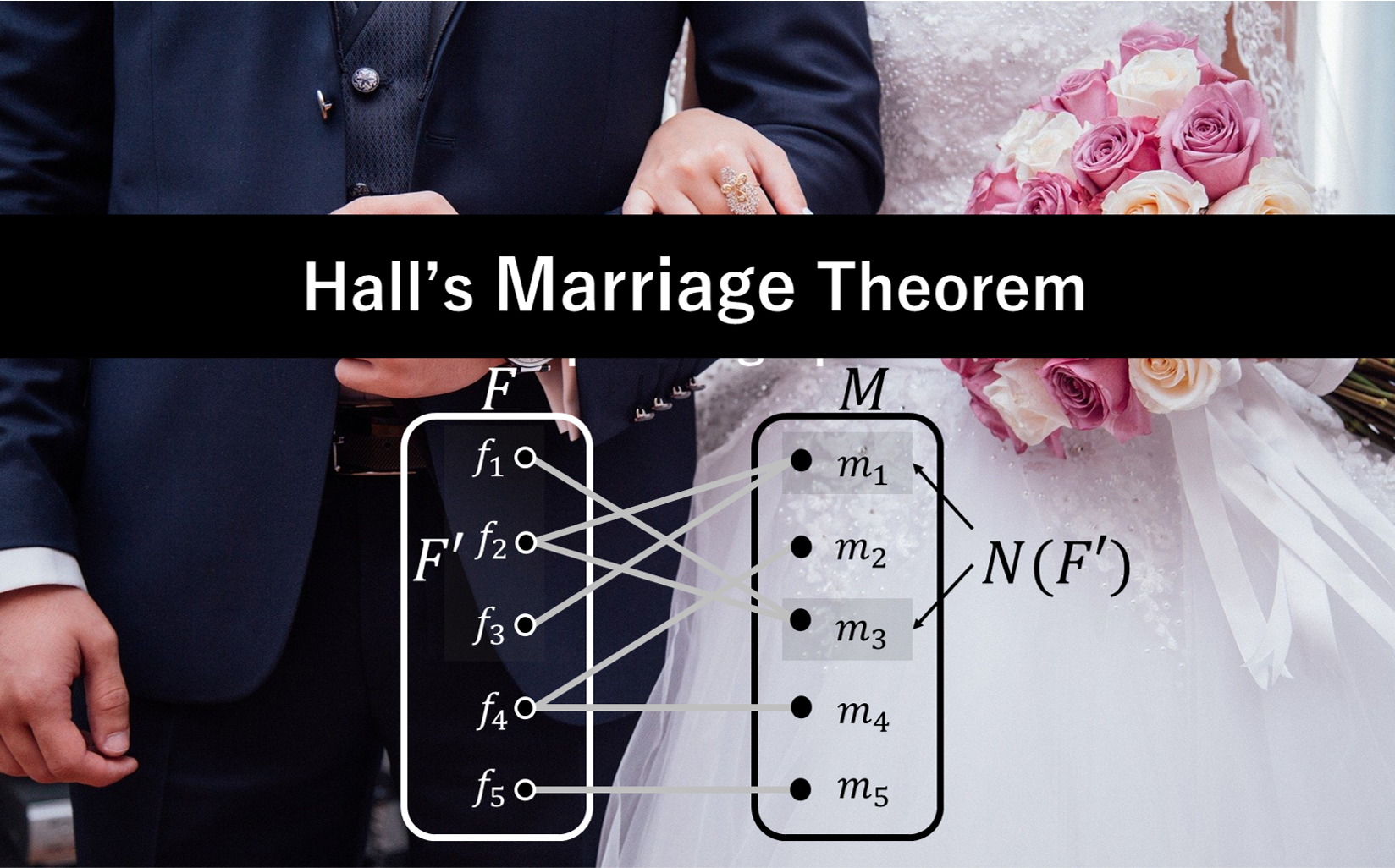
上の状況を一般的に扱えるように文字を使って整理してみましょう。まず、女性グループの集合を\(F=\{f_1, f_2, f_3, f_4, f_5\}\)、男性グループの集合を\(M=\{m_1, m_2, m_3, m_4, m_5\}\)とします。次に女性の要望を以下のように「グラフ」で表現します。
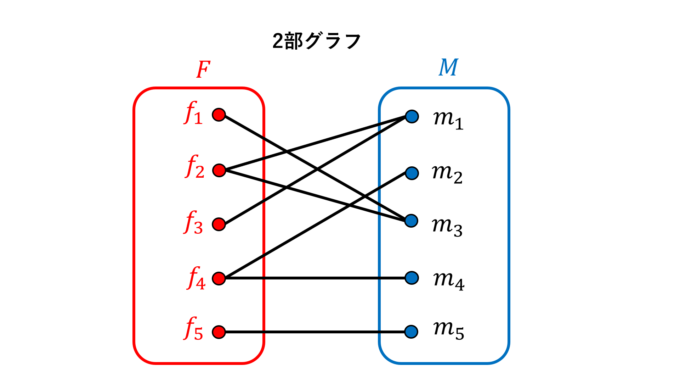
このように、全体を\(F\)と\(M\)の2つに分けることができ、辺が\(F\)と\(M\)のみをつなぐ(\(F\)や\(M\)内でのつながりがない)ようなグラフを2部グラフ(bipartite graph)と呼び、今回のマッチング可能性はこの2部グラフに関する議論になります。
もう少し、記号の準備を行います。例えば、集合\(X\)に対して、\(|X|\)で要素数を表すことにします。例えば、\(F\)の中の\(f_3, f_4, f_5\)で構成される部分集合\(F’\)は要素数3なので、\(|F’|=3\)と表します。また、おなじ\(F’\)で表される女性たちの要望相手の集合を\(N(F’)\)と書くことにします。これは、グラフにおいて、\(F’=\{f_3, f_4, f_5\}\)とつながっている男性の集合\(\{m_1, m_2, m_4, m_5\}\)を表します。

3.ホールの結婚定理
いよいよ、ホールの結婚定理の主張を述べます。
\(F\)の全ての部分集合\(F’\)において常に
\begin{align*}
|F’|\leq|N(F’)|
\end{align*}
が成り立つことと、女性の要望に沿ったマッチングが存在することは同値。
やばくないですか!?
部分的な要望と要素数の大小関係を見るだけで、要望に沿うマッチングが可能かどうかが決定します!!
例えば要望②の例で確認してみましょう。
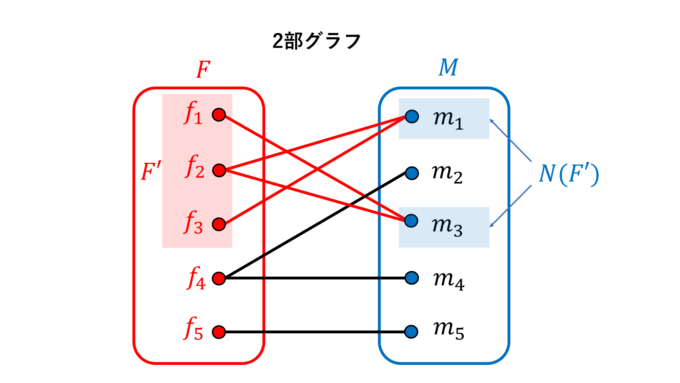
例えば\(F’=\{f_1, f_2, f_3\}\)について考えましょう。このとき\(N(F’)=\{m_1, m_3\}\)となり、要素数が
\begin{align*}
|F’|>|N(F’)|
\end{align*}
となってしまい、結婚定理の条件を満たしません。したがって女性陣全員の要望に沿うようなマッチングは存在しないことがわかります!マッチングが存在することを保証するには、\(F\)の全部の部分集合について大小関係を調査しなければいけません。しかし、結婚定理のすごいところは、1つでも不等号が逆になるものが存在すれば、ただちにマッチングが存在しないことが言えてしまう点です!数学って面白いですね!
4.さいごに
いかがでしたでしょうか?今回は適切なマッチングの可能性を、グラフ理論を使ってその必要十分条件を説明しました。こうした問題は男女のマッチングだけではなく、仕事の振り分けなど、様々な応用が考えられます。なお、実際にマッチングを構成する方法は別の話になるのですが、今後このあたりについての記事もまとめていこうと思います。
今回参考にしたのは、グラフ理論の記事ではもはやおなじみになった和からの講師仁平先生の「グラフ理論序説」です!(個人的にこれはバイブルです)
グラフ理論序説 仁平 政一(著),西尾 義典(著) プレアデス出版
結婚や婚活に興味のある方はこちら
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>















