こんにちは。和からの数学講師の岡本です。今回はゲームについてお話します。例えば囲碁や将棋などはまさに、戦略がものをいいます。現代では、AI（人工知能）を使って「最良の手」などが解析されています。しかしながら、一手一手の手数の組み合わせの数は途方もなく多く、なかなか人間の頭の中で「必勝法」を確定するのは難しいようです。

今回は一例として「石取りゲーム」という１対１のゲームについて考えていきます。

１．石取りゲームとは

　まず、なるべく多くの石を用意します。その石をいくつかの「山」に分けて盤上に置きます。２人のプレイヤーは交互に「山」から石を取っていきます。ただし、取っていく石は何個でも構いませんが、必ず１個以上は取ることと、取る場合は１つの山からのみとします。

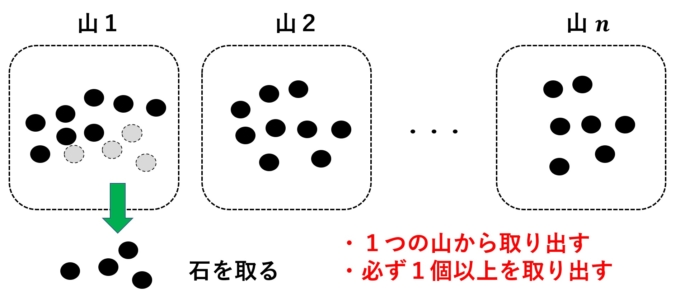
つまり、複数の山から少しずつ石を取っていくことはできません。このルールのもと、最後に石を取ったプレイヤーが勝利とします。
　最も簡単な例として山が１つの時を考えます。

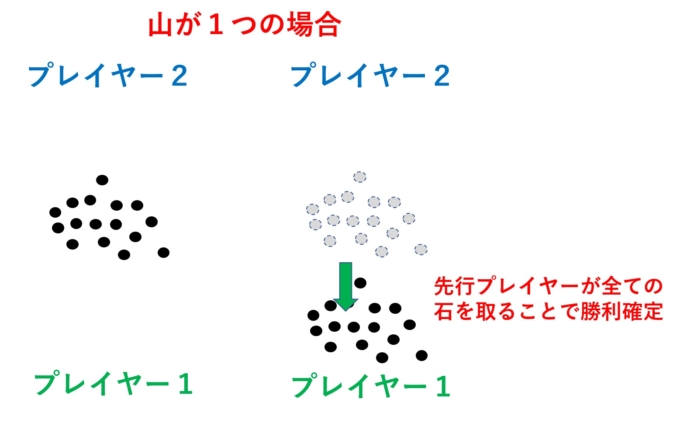
この場合は先手必勝です。最初のプレイヤーが全ての石をもっていけばゲーム終了となり、全く面白くありません。なので、山は２つ以上で考えていくことにします。

２．山が２つの場合でやってみよう！

　山が２つの場合を考えましょう。例えば、石の数7個の山Xと4個の山Yという具合に分けておき、Aさん→Bさんという順番で石取りゲームを始めます。

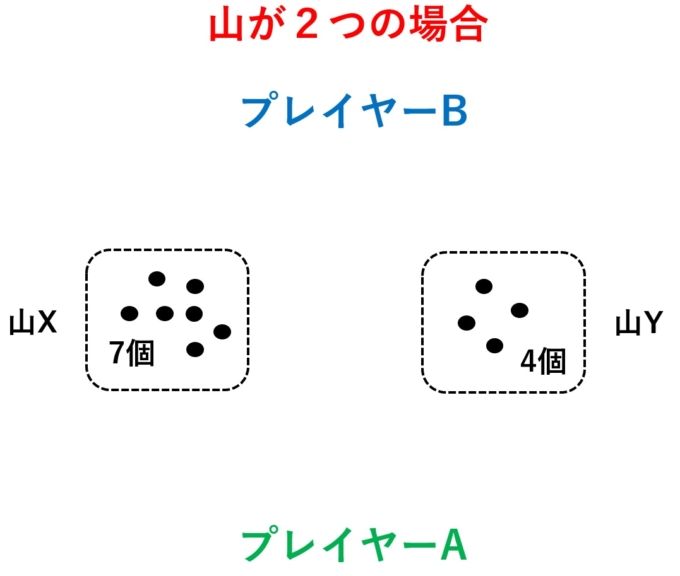
Aさん「まず、山Xから石を２個取ることにします。」

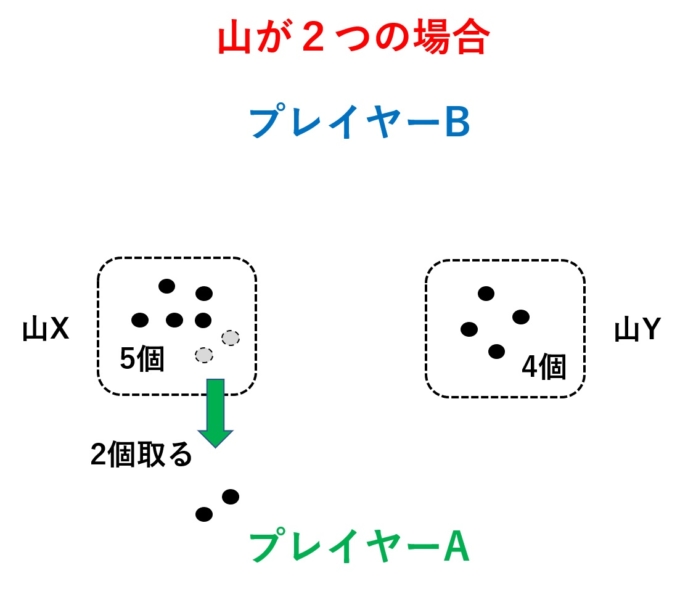
Bさん「では、Xから石を4個取ることにします。」

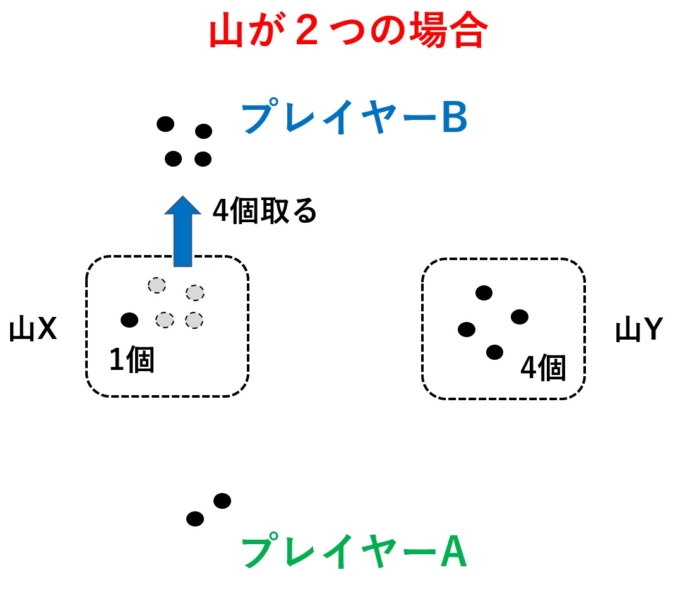
Aさん「う～ん。あ！ひらめいた！では、次はYから3個頂きます！」

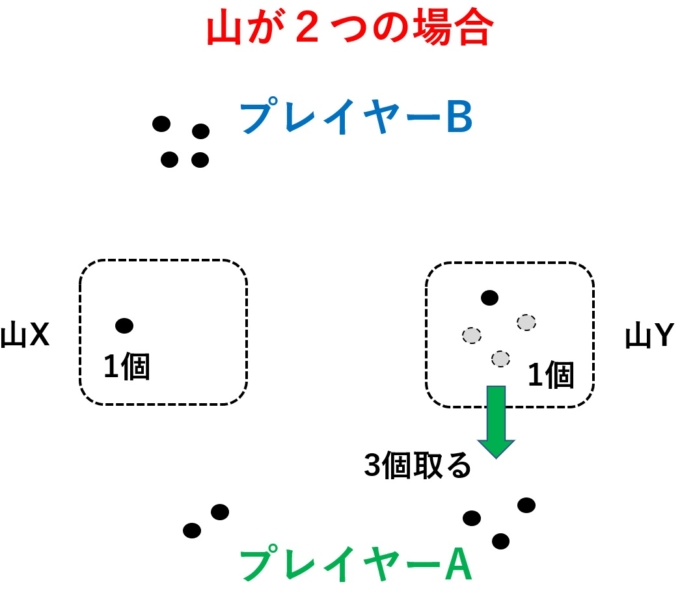
Bさん「あ…、しまった…（泣く泣くYから1個を取る）」

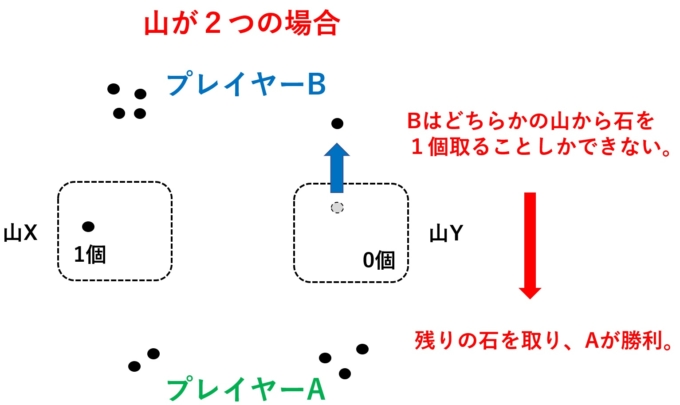
Aさん「では、いただきます！（最後の１個を取り、Aさんの勝利）」

という具合でAさんが勝利しました！

３．戦略を考えてみる

　では、戦略について解説していきましょう。２節のシチュエーションの場合、先方のAさんが優位なのです。それどころか、戦略がわかっていれば、Aさんは必ず勝利できます。

実はこのゲームの必勝方法は「石の数を同じにすること」です。つまり、最初のAさんが７個ある石のうち３個を取ることで石の数のペアを(4, 4 )にします。

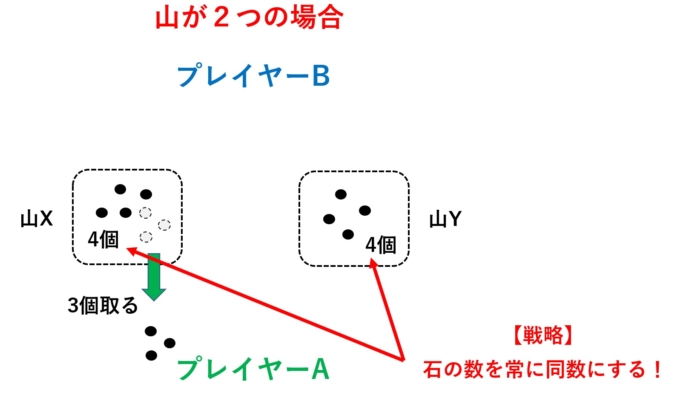
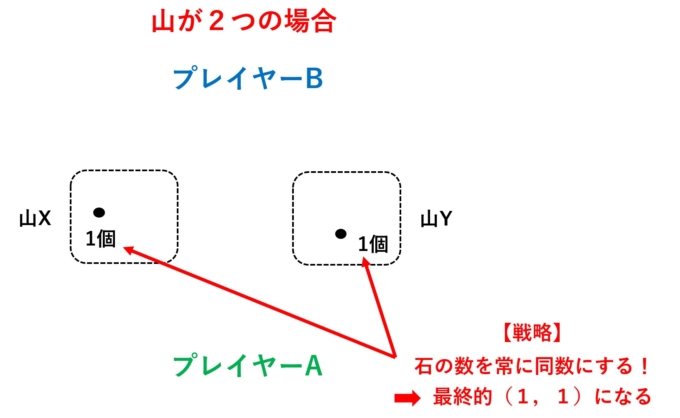
この後、Bさんがどんな手を使っても、Aさんはそれを真似して石の数の多い山から石を取り、同数にすることができます。これを繰り返していくことで、いつか必ず石の数のペア(1, 1)でBさんの番となるはずです。ここまでくれば、もうAさんの勝利は確定します。なぜならBさんは必ず１つ以上の石を取らなくてはいけませんし、１つの山からしか取れないというルールのため、Bさんはどちらかの山から１個石を取ることしか選択肢がありません。よってAさんが最後の石を取ることで勝利します。このような戦略に関する数学的な研究分野として「ゲーム理論」というものがあります。次回以降にもう少し詳しくお話していこうと思います。

５．さいごに

いかがでしたでしょうか？今回は山が２つの場合について、その必勝方法を解説してきました。でもまだまだ物足りないですよね？次回は山が３つ以上の場合について考えます。面白くなってくるのはここからです！果たして最良の手があるのか？「神の一手」は存在するのか！？ぜひ次回もお楽しみに！！

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。

<文/岡本健太郎>