単純比較じゃダメ?“境目分析”で因果を探る回帰不連続デザイン【Part1】
公開日
2025年9月17日
更新日
2025年9月19日

この記事の主な内容
因果推論って何?
私たちが日々のビジネスで直面する大きな課題のひとつが、「施策の効果をどうやって測るか」という問題です。広告、キャンペーン、値引き、クーポン、SNS施策、どれも成果を上げるために取り組みますが、施策の効果、つまり「その施策がなければ結果はどうなっていたのか」 を知ることは難しい問題となります。
この「もし施策をしなかったらどうなっていたか?」を推定する学問分野が 因果推論(Causal Inference) です。因果推論は単なる相関や平均の差ではなく、「施策が結果を変えたのか?」を見極めるための枠組み なのです。
単純な比較だとだめなの?
施策の効果を測るためには施策のあり、なしで結果がどうなるかを比較すれば良いように思えます。このような単純な比較で施策効果を測ることは多くの場合問題があることが知られています。
たとえば、ある企業が広告キャンペーンを実施したとしましょう。広告を出した店舗の平均売上は、出していない店舗よりも高かったとします。一見すると「広告の効果があった」と思えますが、実はそう単純ではありません。

この方法で施策の効果を見積もってしまうと正しい見積もりにならない可能性が高いです。なぜならば比較する対象が全く同じだと考えることができないからです。
- 店舗規模の違い:広告を出したのは大型店で、もともと売上が高い
- 顧客層の違い:クーポンを送ったのは上位顧客で、購買頻度が高い
- 立地条件の違い:広告実施店舗が駅前に多い
両者に施策の有無以外の違いがあった場合、売上の差が「広告の効果」なのか「もともとの条件の違い」なのかが分からなくなるのです。このように単純に2つのグループを比較するだけでは、本当の因果効果を正しく測れないのです。
では、どうすれば正しく因果効果を測れるの?
そこで登場するのが、ランダム化(Randomization)という考え方です。ランダム化とは、施策の「あり/なし」を無作為に割り当てる方法で、たとえば店舗をランダムに2つのグループに分け、一方にのみ広告を実施するといった形です。
ランダムに分けることで、店舗規模や立地、顧客層といった施策以外の要素が2つのグループ間で平均的に等しくなると期待されます。つまり、施策の有無以外の条件が揃った状態になるため、売上の差が施策の効果によるものだと、より自信を持って言えるようになるのです。
このような「ランダム化比較試験(Randomized Controlled Trial, RCT)」は、因果推論の中でも最も信頼性が高い方法とされています。医学やマーケティング実験などでも多く使われています。
しかし、現実のビジネスの現場では、全ての場面でランダム化を行うことは難しいことも多いでしょう。倫理的な制約やコスト、運用上の制限があるため、ランダムにグループ分けできないケースがたくさんあります。
そこで登場するのが、「自然に起きた違い」をうまく利用して因果関係を推定する手法です。たとえば、特定の数値を境に施策の対象が変わる場合に活用できるのが、次に紹介する回帰不連続デザイン(Regression Discontinuity Design)です。
回帰不連続デザイン
この手法の発想はシンプルで、「境目(しきい値)」に注目して比較する というものです。
例えば、上記の状況で
・「従業員が50人以上の店舗だけ広告を実施する」
というルールで施策を行っていた場合、つまりある数値に閾値を設定し、その数字が閾値を超えるか否かで施策の有無が決まるという場合に回帰不連続デザインを使用することができます。
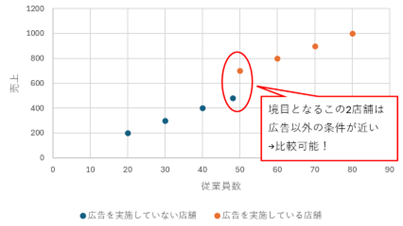
今回の状況では、施策を行った店舗は平均的に従業員が多く、施策を行わない店舗は従業員が少ないという違いが存在するので、単純な比較をすることは良くないでしょう。
そこで注目するのは ギリギリ広告なしに振り分けられた店舗(従業員が50にギリギリ満たない) と ギリギリ広告ありに振り分けられた店舗(従業員がギリギリ50を超える) です。
両者の従業員数はほとんど同じですから、従業員数に関しては両者は似ています。従業員数が同じような店舗が、1人、2人のわずかな従業員数の違いによって施策を行うグループに入ったり、施策を行わないグループに入ったりと、2群はある程度偶然性をもって作成されていると考えることができるでしょう。つまりこの境界の付近ではランダム化が行われているとみなして比較を行うのです。この「境目の前後だけに注目して因果効果を推定する」という考え方が、回帰不連続デザインの考え方です。
例えば従業員数が49人の店舗と50人の店舗を集めて、これらの2群を比較します。2つのグループは疑似的なランダム化が行われているとみなしますから、2群に結果の差が表れていればそれは施策の影響だろうと考えるのです。
アイデアをとらえることが重要
このような因果推論の手法は数学を元に成り立っています。そのため、これを数学的に学ぼうとすると初学者の方には非常にとっつきにくく感じてしまうかもしれません。
しかし、回帰不連続デザインに限らずに、データ分析の手法は問題を解決するためのアイデアからスタートし、それを数式で表現するような成り立ちが多いです。
そのため初学者の方は、いきなり数学から学ぶのではなく、その手法を特徴づけるアイデアから学ぶことをお勧めします。今回の回帰不連続デザインだと、「2群は似ているとは言えないが、ある数値の境目の前後は似ているだろう」というアイデアがもとになっています。
データ分析の手法を学ぶ際には、この点をとらえることを意識するとより良いのではないかと思います。
因果推論の多くの手法は数学に支えられています。そのため、数式から学び始めると初学者の方にはとっつきにくく感じられがちです。とはいえ、回帰不連続デザインに限らず、データ分析の方法は「現実の問題をどう解くか」という発想が先にあり、のちにそれを数式で定式化してきたものが少なくありません。だからこそ学び始めは、数式よりもまず“その手法を成立させているアイデア”に焦点を当てることをおすすめします。
たとえば回帰不連続デザインのアイデアは、「集団全体では二つの群は同質とは言えないが、ある数値の境目(閾値)の直前と直後にいる対象は条件がほぼ同じとみなせる」という考え方です。
この
“発想 → 数式化 → 推定手順”
の順で理解していくと、理解が速く、応用もしやすくなります。
データ分析の手法を学ぶ際には、この観点を意識して進めるとよいでしょう。
セミナーのご案内
今回ご紹介した「回帰不連続デザイン」は、ビジネスや政策評価の現場で大きな力を発揮する因果推論の代表的な手法です。
当社では、回帰不連続デザインを実務データで体験できるセミナー を開催しています。数学が苦手な方でも安心して学べるように、数式を極力使わずに直感的な理解を重視したカリキュラムになっています。実際のマーケティングデータを題材に、Rを用いた実装まで体験できますので、学んだ知識をそのまま業務に応用していただけます。
ぜひこの機会に、因果推論の考え方と回帰不連続デザインの実践を体験してみませんか?
詳細・お申込みは以下のリンクからご覧いただけます。












