「収束性」の華麗なる言い換え
公開日
2021年3月29日
更新日
2021年3月29日

こんにちは。和からの数学講師の岡本です。今回は以前お話した「収束」に関する話題です。
数列\(a_n\)が点\(\alpha\)に「収束する」ということは、極限記号を使って
\begin{align*}
\lim_{n\to \infty}a_n=\alpha
\end{align*}
と表すことができますが、\(\varepsilon\)-\(N\)論法を使うことで次のようにより厳密に表現できます。
\begin{align*}
\forall \varepsilon >0, \exists N \in \mathbb{N}, \mathrm{s. t.} n\geq N \Longrightarrow |a_n-\alpha|<\varepsilon .
\end{align*}
しかし、この表現方法は収束先\(\alpha\)がわかっていることが大前提であり、「数列\(a_n\)がどこかに収束すること」を表現することはできません。大学入試問題でも収束先(極限値)を求める問題があるぐらいで、収束先がわからないことは少なくありません。そこで、今回の記事では、「数列(完備距離空間内の点列)の収束」の別表現について解説していきます。なお、数列の収束(\(\varepsilon\)-\(N\)論法)に関しては以前のマスログをご覧ください。
この記事の主な内容
1.Cauchy列
次のような性質をもつ数列\(a_n\)をCauchy列とよびます。
\begin{align*}
\forall \varepsilon >0, \exists N \in \mathbb{N}, \mathrm{s. t.} n, m\geq N \Longrightarrow |a_n-a_m|<\varepsilon .
\end{align*}
これは、「フランスのGauss(ガウス)」とも称されたフランス人数学者オーギュスタン=ルイ・コーシー(下図)に由来しています。

さて、Cauchy列、なんだか\(\varepsilon\)-\(N\)論法による数列の収束性ににています。日本語に訳してみると、「任意の正の実数\(\varepsilon\)に対して、ある自然数\(N\)が存在し、\(n,m\)がこの\(N\)より大きい番号であれば数列間の差\(|a_n-a_m|\)は\(\varepsilon\)より小さくなる」と言っています。つまり、「どれだけ小さなものさし\(\varepsilon\)を持ってきても、ある程度大きな番号同士の差はこのものさしより短くなる」(→「どんぐりの背比べ」と思っても大丈夫です)という意味です。実は数列\(a_n\)が\(\alpha\)に収束する場合、\(a_n\)はCauchy列となることが容易に分かります。実際に
\begin{align*}
\forall \varepsilon >0, \exists N \in \mathbb{N}, \mathrm{s. t.} n, m\geq N \Longrightarrow |a_n-\alpha|<\varepsilon , |a_m-\alpha|<\varepsilon
\end{align*}
となるので、同じ\(\varepsilon\)と\(N\)に対して
\begin{align*}
|a_n-a_m|=|a_n-\alpha+\alpha-a_m|\leq|a_n-\alpha|+|a_m-\alpha|<2\varepsilon
\end{align*}
となり、\(\varepsilon\)が任意であることから\(2\varepsilon\)も任意なので、数列\(a_n\)はCauchy列となることがわかります。
このように、収束列であればCauchy列であるという関係がわかりました。イメージとしては収束列の外側をCauchy列たちが囲む感じです。
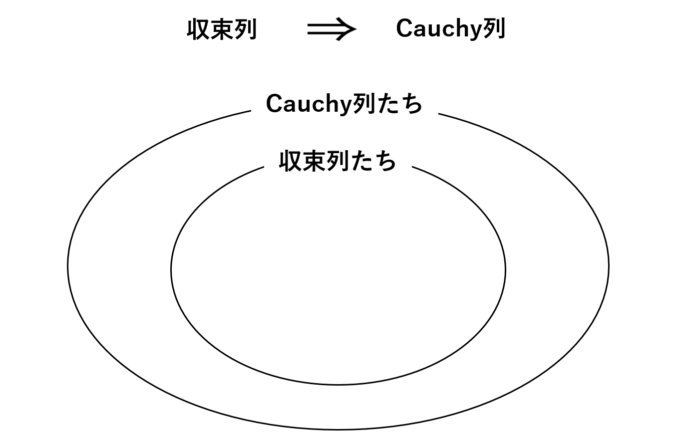
しかし、次節で衝撃の事実が発覚します…!
2.Cauchy列ならば、収束列である
タイトルにもあるように、なにを隠そう、Cauchy列であれば収束列となることが証明できます…。つまり、この事実により「Cauchy列であることと収束列であることが同値」であることが従います。衝撃ですよね。この内容を知った当時、食べていたポッキーを床に落としてしまったほど衝撃を受けました。
考えてみれば、Cauchy列の定義には収束先の情報がありません。つまり、どこに収束するかわからなくてもCauchy列の流儀を使って数列の収束性を厳密に表現することが可能なのです!!
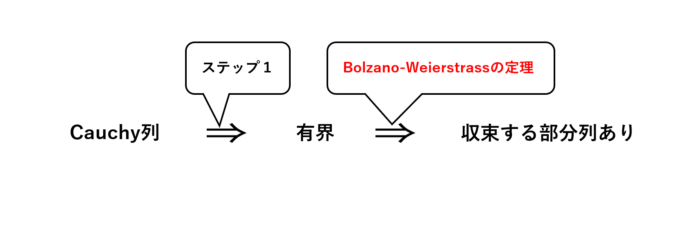
3.脅威のBolzano-Weierstrassの定理
Cauchy列であれば収束列であることの証明の概略をお話します。その際に何度も助けてくれる頼もしい助っ人をご紹介します。その名も「Bolzano-Weierstrass(ボルツァーノ・ワイエルシュトラス)の定理」。その定理の内容は以下です。
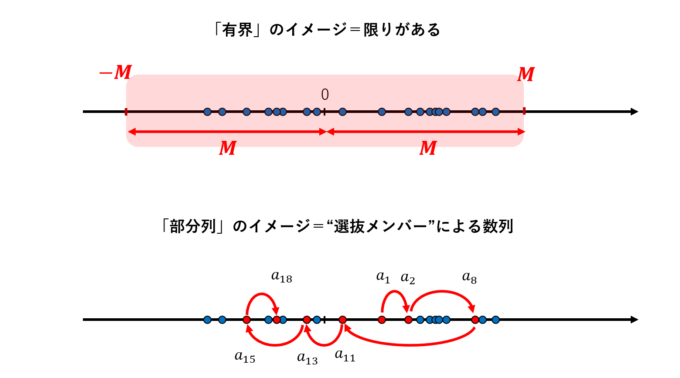
有界な数列は収束する部分列をもつ。
かっこいいですね…。シンプル過ぎて何言ってるのかわからなくなってしまいますが、間違いなく「大定理」の1つです。すこし補足してみます。まず「有界」というのは、「限界が有る」ということです。つまり、「数列が有界である」とは「プラス方向やマイナス方向に行きすぎず、必ず限度があるということ」(→「袋のなずみ」と考えても大丈夫です)です。数式を使うと、ある実数\(M>0\)が存在し、\(|a_n|>M\)という具合に数列たちを\(\pm M\)で閉じ込めることができることを意味します。次に部分列についてですが、以下の図のように、数列の一部を取り出してできる「部分的な列」つまり「“選抜メンバー”による数列」のことをいいます。
では、Bolzano-Weierstrassの定理を使って「Cauchy列ならば収束列」の証明の概略を説明します。論理(ロジック)の律動(リズム)に酔いしれましょう…!
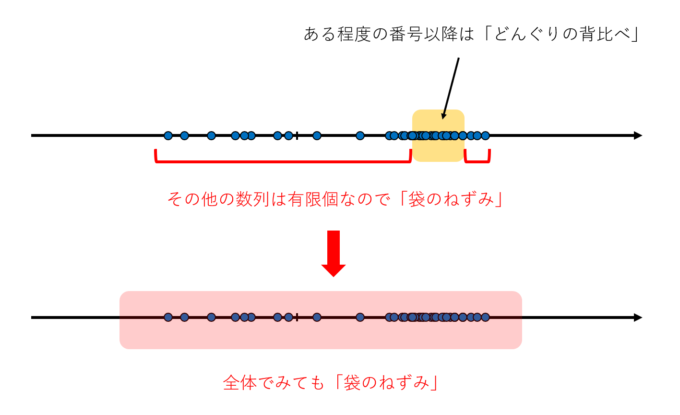
【第1ステップ】まず、数列\(a_n\)がCauchy列であるとします。このとき、どんな\(\varepsilon>0\)に対しても\(N\)番目以上の番号の差は\(\varepsilon\)で押さえられます。言い換えると、「ある程度大きい番号同士は“どんぐりの背比べ”」という感覚です。また、\(N\)番目未満の数列に対しても高々有限個なのでやはり「袋のねずみ」です。つまり、Cauchy列は有界であることがわかります。
【第2ステップ】Cauchy列\(a_n\)は有界であることがわかったので、Bolzano-Weierstrassの定理により、\(a_n\)はある値(例えば\(\alpha\)としましょう)に収束する部分列を持つことが保証されます。
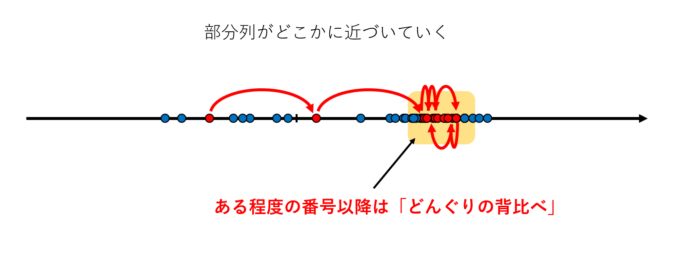
【第3ステップ】Cauchy列が\(\alpha\)に収束する部分列を持つとしましょう。このとき収束性の定義から、ある程度大きい番号の部分列は\(\alpha\)周辺に入っていきます。しかし、\(a_n\)はCauchy列なので、ある程度大きい番号同士の差は限りなく小さくなります。つまり、\(a_n\)自身も自動的に\(\alpha\)に近づいていくことがわかります…!!
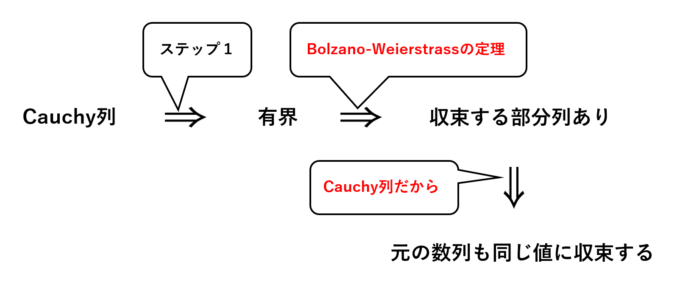
以上のステップにより、\(a_n\)はCauchy列であれば収束列であることが証明されます!たまらんですね…!
4.さいごに
いかがでしたでしょうか?今回は大学で習うような収束性に関する話題をご紹介しました。このような論理の美しさを1から味わっていきたい方は是非和からの個別授業を!
今回の内容に関してオススメの参考書はこちら!
大学初年度の微分積分の内容が詰まっていて非常に面白いです!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>