こんにちは。和からの数学講師の岡本です。前回に引き続き、ウミガメのスープについてお話をしていきます。前回のマスログでは、ウミガメのスープのルールについて簡単に解説いたしました。今回は数学を使った「グラフ理論版ウミガメのスープ」についてお話をしていきます。なお、このゲームは岡本オリジナルです。

１．ウミガメのスープの復習

さて、まずはウミガメのスープについて簡単におさらいしておきます。このゲームは出題者と、複数の回答者に分かれて行います。詳しいルールについては前回の記事をご覧ください。ざっくりいうと、出題者はある大きな出来事を部分的に説明し、全容がどうなっているのかを問います。もちろん一発ではなかなか答えられないので、ヒントを散りばめて答えに導いていきます。

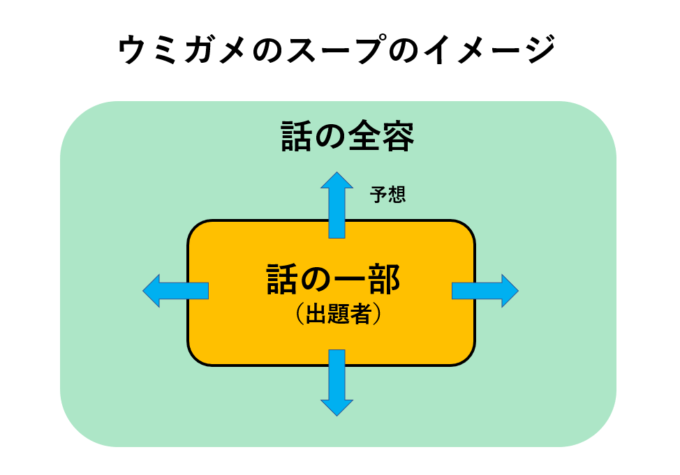
これをグラフ理論バージョンとして発展させていきます。

２．グラフ理論版を考える

グラフとは以前もマスログ何度か取り上げましたが、「頂点と辺とそのつながり具合の情報」の事を言います。それをビジュアル化したのが以下のようなものです。この図のことを単に「グラフ」と呼んでも構いません。

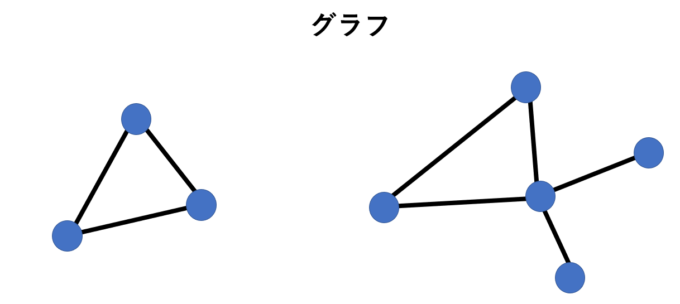
さて、グラフ理論版のウミガメのスープとは、シンプルに説明すると以下のような流れです。

①出題者は１つのグラフを用意します。
②出題者はグラフの簡単な特徴を一部公開します（例えば頂点の個数や辺の個数）
③回答者は元のグラフの形を予想します。
④先に正しいグラフの形を解答した人が勝利です。

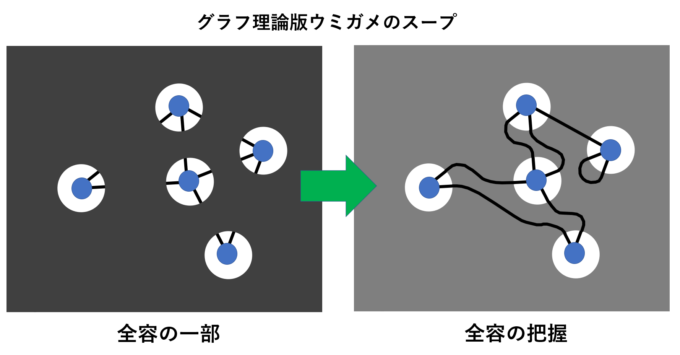
いかがでしょう？意外とシンプルではないでしょうか。しかし、「グラフの特徴」を利用するわけですから、グラフの基本的性質や知識が必要になってきます。

３．グラフ理論入門

この節ではグラフを数学的に扱います。まず、頂点(vertex)の集合を\(V\), 辺(edge)の集合を\(E\)とします。先ほどの説明の通り、グラフとは、頂点と辺のつながり具合の情報を表します。そこで、辺を２つの頂点のペアとして考えます。こうすることで、頂点の集合\(V\)とそのつながりの情報を含んだ辺の集合\(E\)のペアがグラフ(graph)となり、\(G=(V,E)\)と表します。
例えば、\(V=\{v_1, v_2, v_3\}\)とし、辺を\(E=\{v_1v_2, v_2v_3, v_3v_1\}\)と表します。すると\(G\)は

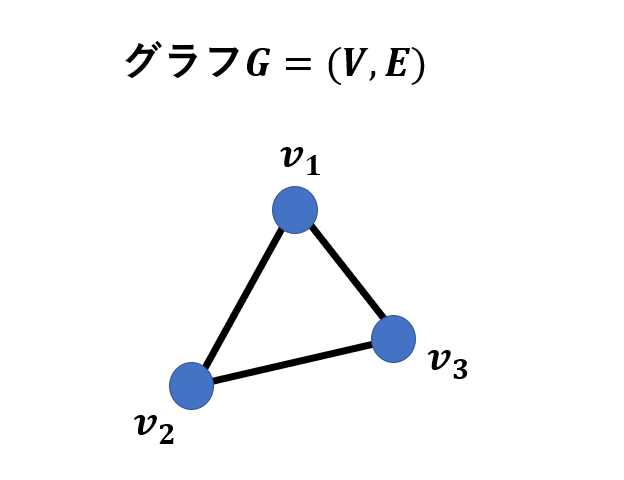
という形に対応します。なお、グラフとはあくまで「つながり」の情報しかないので、辺の長さや、頂点の位置は全く気にしなくても構いません。例えば、以下の図はどれも上の例のグラフ\(G\)を表します。

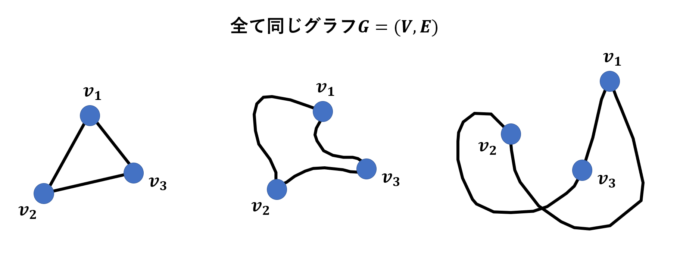
さらにグラフについて基本的な用語をまとめておきましょう。同じ頂点から同じ頂点に帰ってくる辺のことをループ(loop)といい、２つの頂点を結ぶ辺が複数存在するとき、多重辺(multi-edge)といい、多重辺を含むグラフを多重グラフ(multigraph)と呼びます。頂点、辺の数がともに有限個であるようなグラフを有限グラフ(finite graph)と言います（今回は有限グラフのみを扱います）。また、頂点から出ている辺の本数をその頂点の次数(degree)といい、ループの場合は２とカウントします。

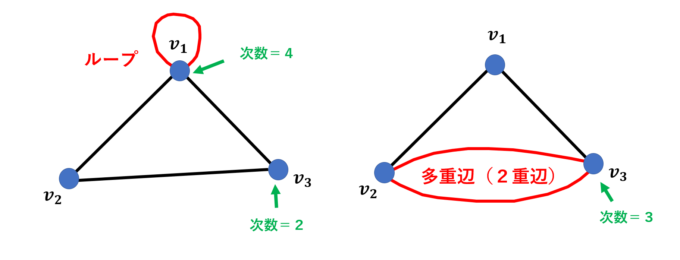
グラフ内の辺を連続して結んだものを道(path)と呼び、始点と終点が同じになるような道をサイクル(cycle)と言います。そして、与えられたグラフの任意の頂点を結ぶ道が必ず存在するとき、そのグラフは連結(connected)であると言います。

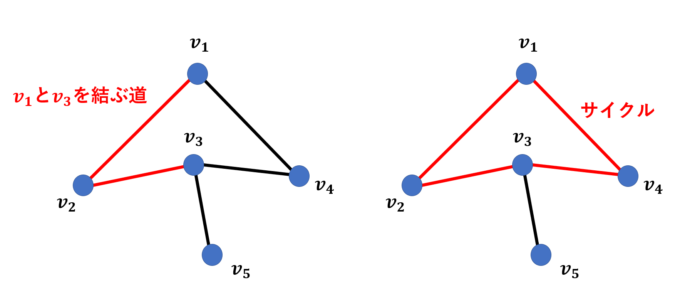
次に、２つのグラフ\(G\)と\(H\)を考えます。つながり具合を保存したまま\(G\)の頂点を\(H\)の頂点に１対１に対応させることができるとき、グラフ\(G\)と\(H\)は同型であるといいます。シンプルに言うと、「形が同じ」というだけです。

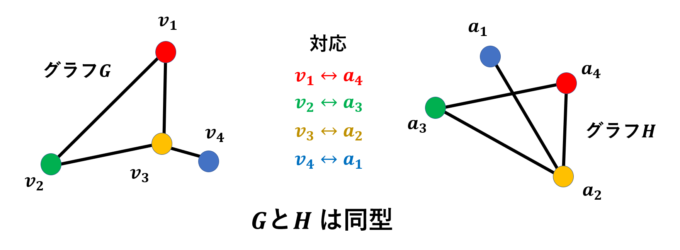
これらの用語を駆使することで、グラフ理論版ウミガメのスープが実現できます。

４．グラフ理論版ウミガメのスープ『グラフのスープ』

ではいよいよ、３節で解説したグラフの用語を使い、ゲームを行っていきます。出題者の最初の説明により、無数のグラフの候補はやや絞られます。ヒントが増えていくごとに、候補の上限が下がり、最終的なグラフの形が決定できます。そのため、候補が縛られたところでいかに早く正確なグラフを描写できるかにかかっています。また、上限は数学用語で、「sup（スープ）」と表すことから、このゲームは岡本によって『グラフのスープ（sup）』と名付けられました。

では「グラフのスープ」の仮想対戦をもって終わりにしたいと思います。

回答者１「このグラフはconnectedですか？」

出題者「Yes！グラフはつながっています」

回答者２「このグラフはcycleを含みますか？」

出題者「No！いい質問です！このグラフにサイクルはありません」

回答者１「回答します！グラフはこれですか？」

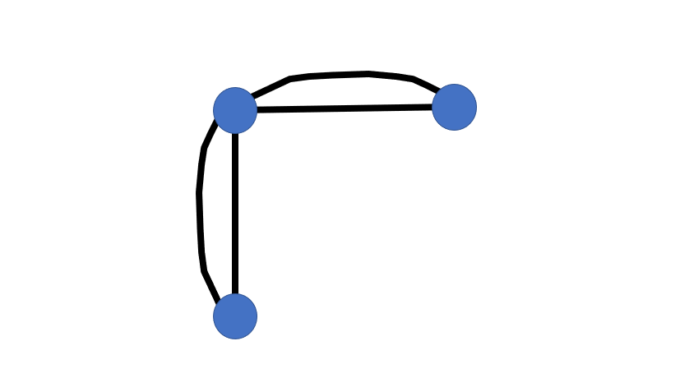
出題者「残念！！違います！回答者１さんは１回休みです。」

回答者２「このグラフにはloopがありますか？」

出題者「Yes！ループは必ずあります！」

回答者２「回答します！グラフはこれですか？」

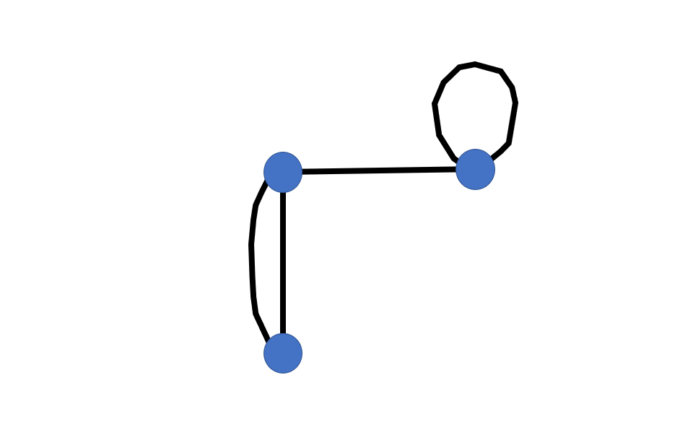
出題者「残念！！違います！回答者２さんは１回休みです。」

回答者１「このグラフにはmulti-edgeがありますか？」

出題者「No！いい質問です！実は多重辺はありません！」

回答者１「回答します！グラフはこれですか？」

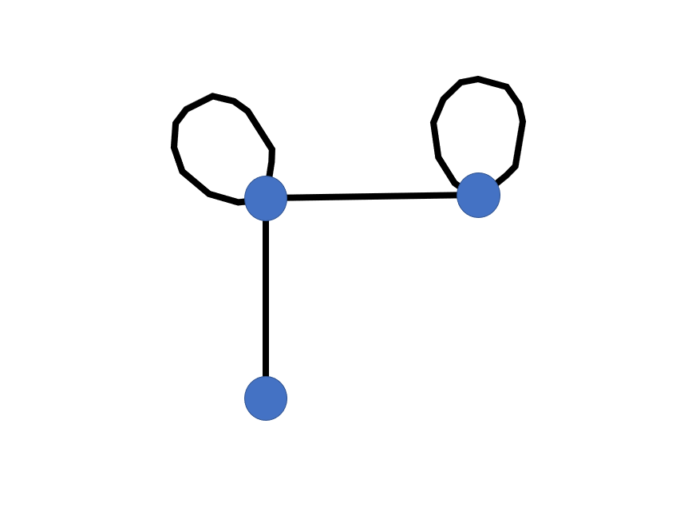
出題者「お見事！同型です！！」

ということで、出題者が設定していたグラフは上のような形だったわけです。全容がわかると確かに回答者と出題者の問答が正しいことがわかります。なお、グラフの形は見た目上一通りではないので、同型なグラフを導きだすことがゴールとなります。そのため回答者が正解したときは「同型です！」と高らかに叫びます。

５．さいごに

いかがでしたでしょうか？「ウミガメのスープ」も面白いゲームでしたが、この「グラフのスープ」もいい線いっているんじゃないかと個人的には思います。なお、このゲームはグラフ理論の理解にもつながるので、いつかアプリゲーム化できたらいいなと思っています。グラフ理論の本のオススメとして以下の書籍を挙げておきます。

レクチャー離散数学 木本 一史 (著) サイエンス社

グラフの基本的な性質をわかり易くまとめてあります。

<文/岡本健太郎>