こんにちは！2020年5月30日(土)にロマンティック数学ナイトがなんと初のオンラインで開催されました。

全国から数学好きが参加！初のオンライン開催！ロマンティック数学ナイト！

今回はプレゼンターの一人、弊社講師兼切り絵アーティストの岡本の発表内容をご紹介します。

 

１　席替えとは

皆さんは席替えと聞いてどんなことが浮かびますか？ドキドキ？わくわく？人によっては、青春の甘酸っぱい思い出の１ページにもなっているかもしれません。今回はこの「席替え」について数学的に考察していきます。

さあ、数学的に考察といえば、まずは定義！早速Wikipediaで調べてみました。

席替え

ちゃんと定義があったんですね！びっくりです。難しく書いてますが、たとえば単純に考えて１～４と番号のついた箱を並べ変えることと同じです。

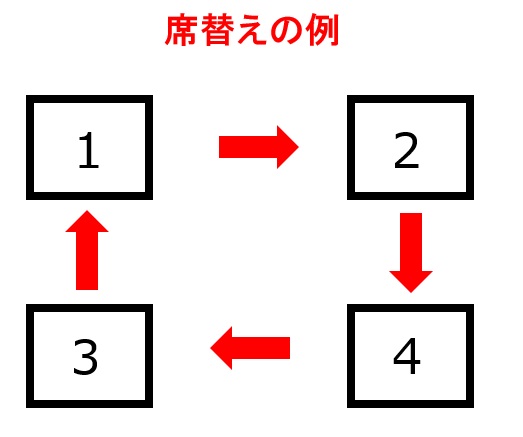
ではここで問題です。

これは実は４！通りあります！「！」は階乗の記号です。つまり４！＝２４通りということです。感嘆符と混同しないようにしましょう！（感嘆符）

では次の問題はどうでしょう？

これは結構難しくて、答えは９通りなんですね。もう少し一般に次のような結果が知られています。

\(n\)席の入れ替えについて

意外と難しい数学の世界に入ってきました。ちなみに「適当に席替えをしたとき、全部の席が入れ替わっているような確率」は

\begin{align*} \frac{M_n}{n!}=\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}+\cdots +(-1)^{n}\frac{1}{n!} \end{align*}

となり、\(n\)が十分大きいとき、この確率は\(e^{-1}\)=約36.7％に近づきます。\(e\)はネイピア数です。つまり、クラスで（公正な）席替えが行われた場合、36.7％の確率で全員が席を動くことになります。面白いですね！

２．メインの話はここから

ここまでで十分に数学の問題として面白い（実際にモンモール数は難関大の入試問題にも現れます）のですが、まだまだ序章にすぎません。いままでの席替えは始まりの位置と結果の位置のみにしか注目していませんでした。

 

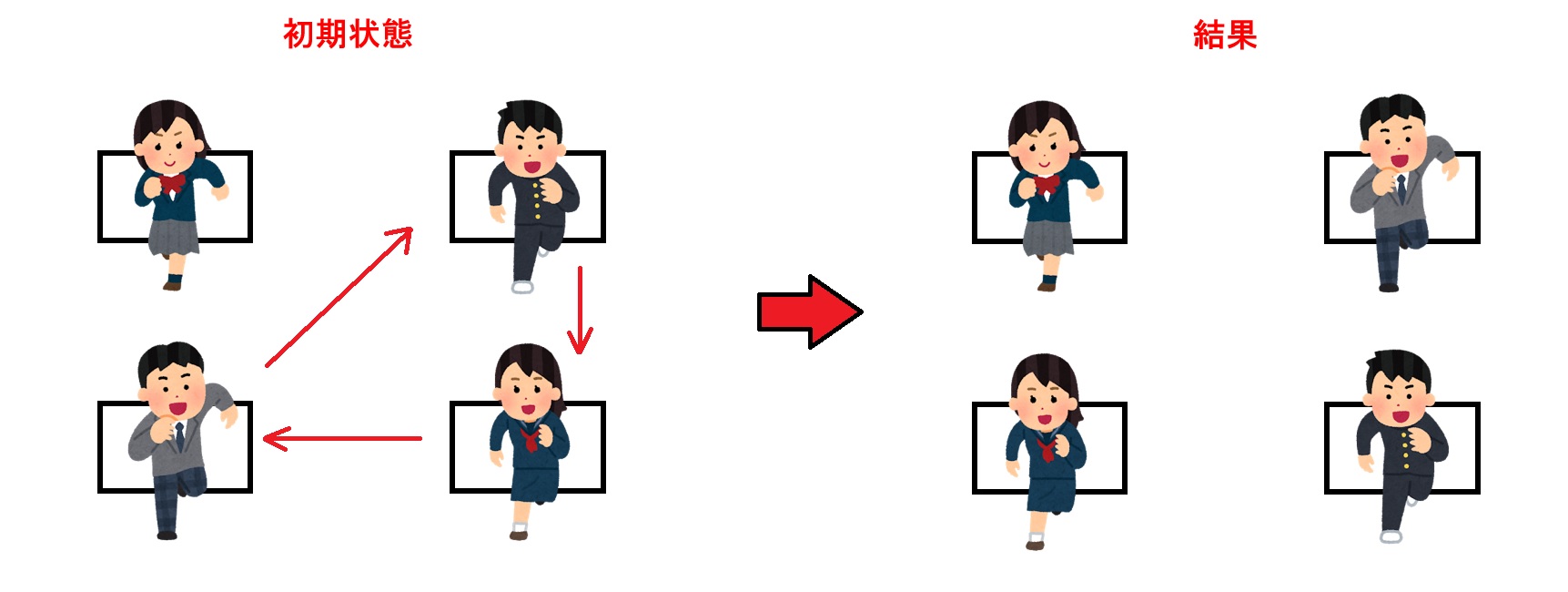
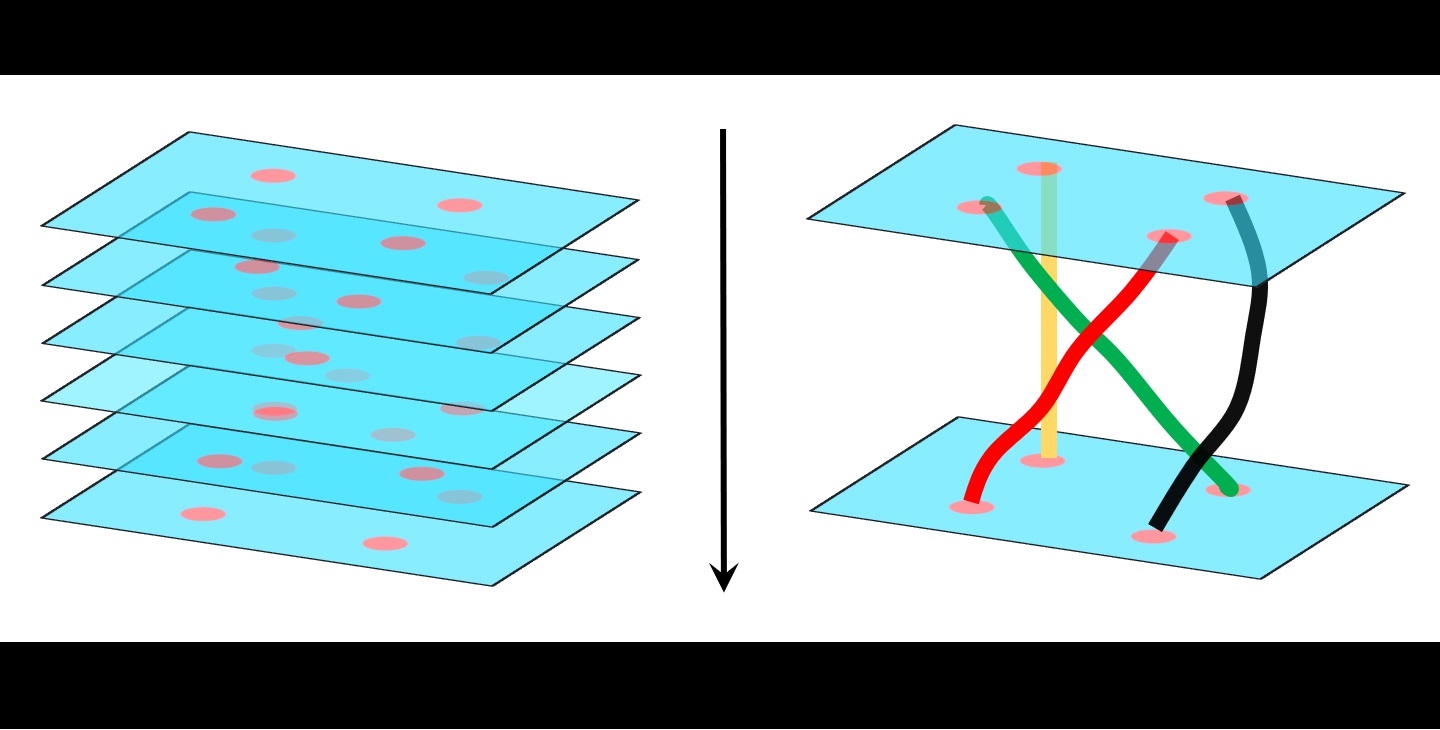
ここでは次のステップとして「時間変化」を考えます。つまり席を移動している生徒の途中の動きの情報も込みで考えます。たとえば次の２つの動きを考えます。

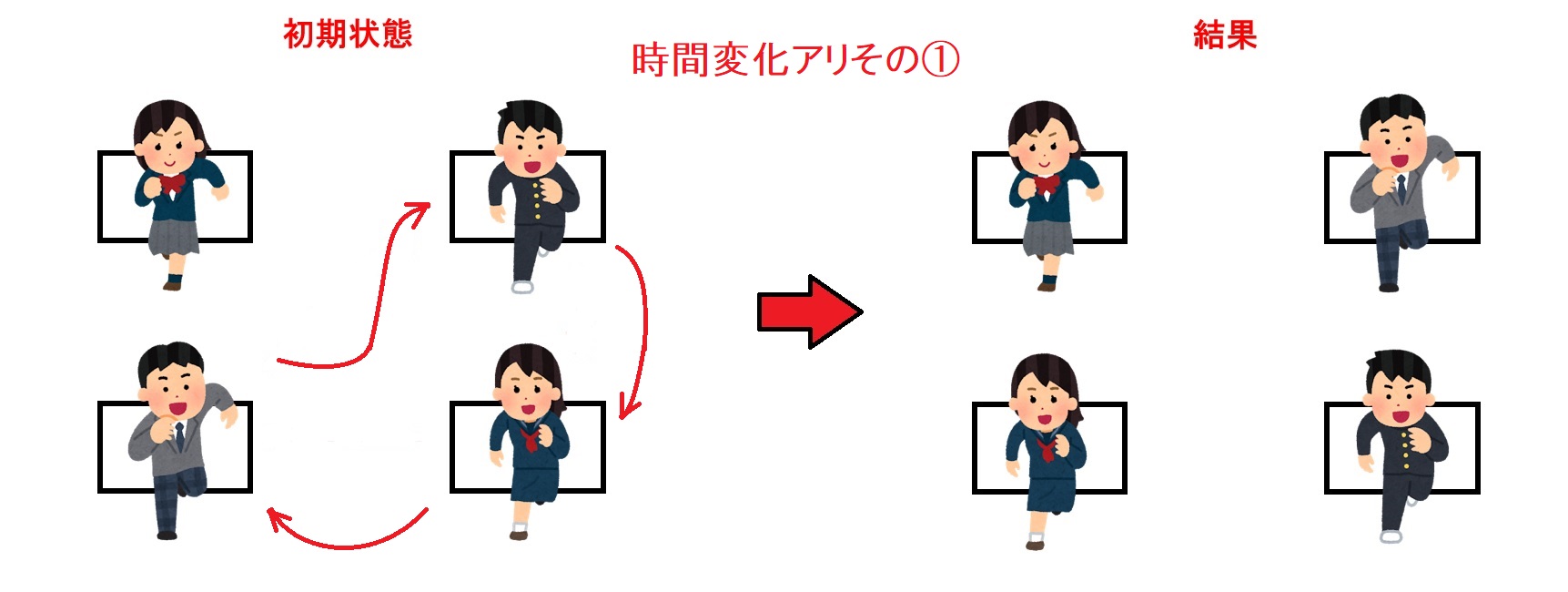
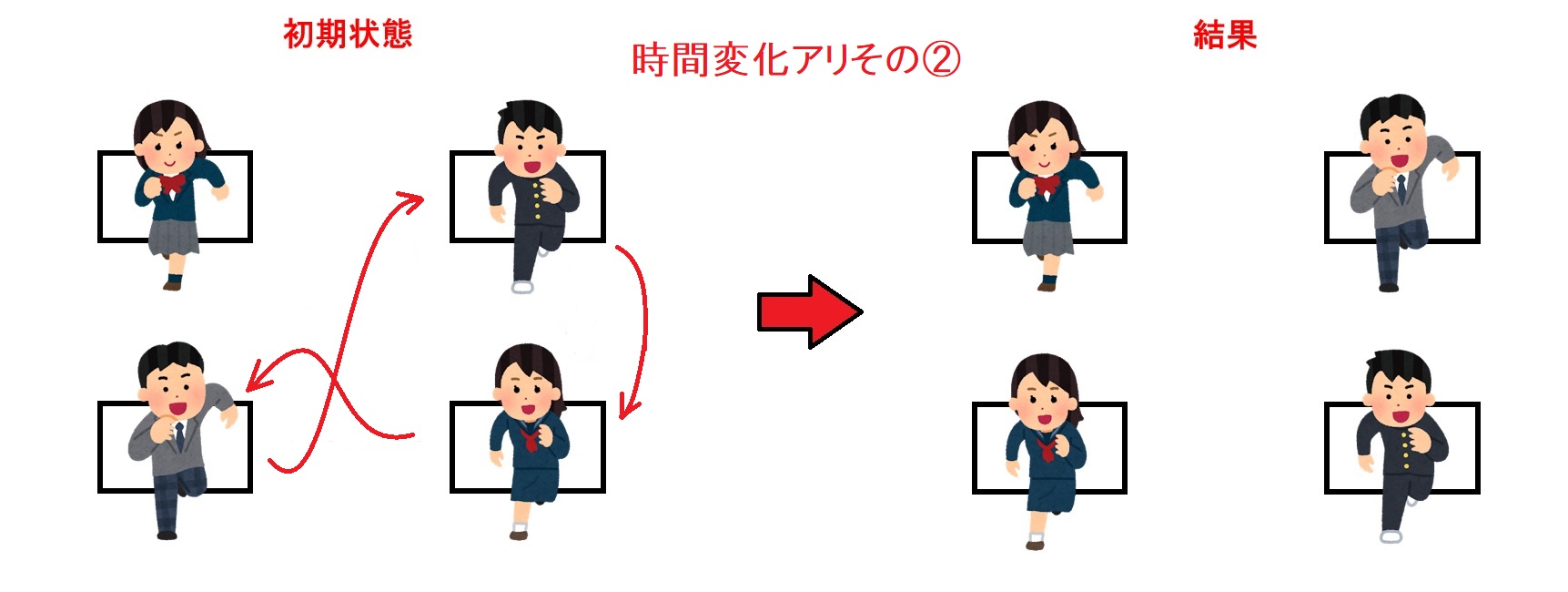
これら２つの席移動は結果として同じ席替えになっていますが生徒の動きが若干違います。こういった「違い」をとらえるために、席の移動を時間軸を使って立体視します。

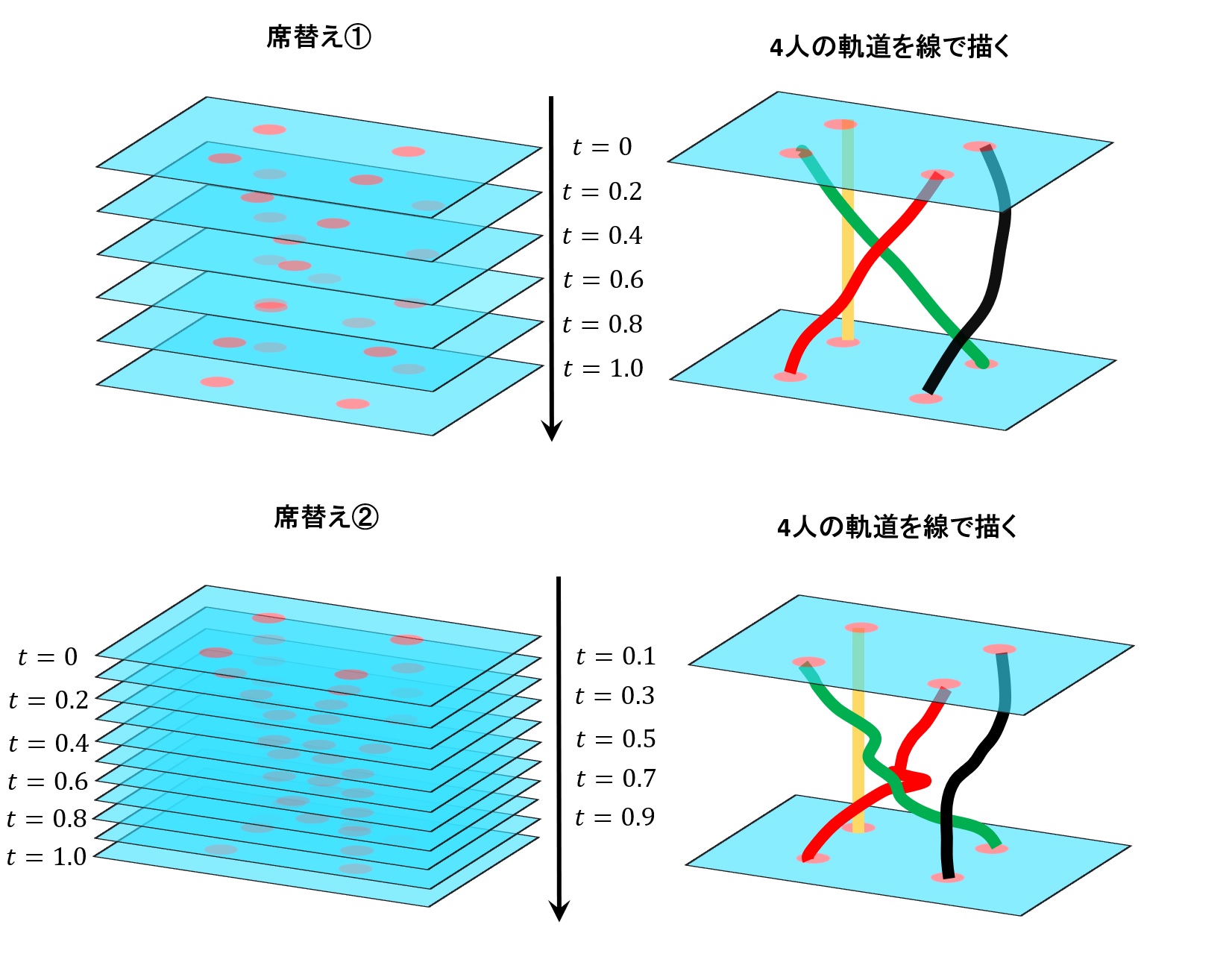
このように４人の軌道を紐としてとらえることで「組み紐群」という数学的対象が現れます。特にこのような「２次元の空間の配置変化」からの定式化を「配置空間の基本群」として得ることができます。

位相空間\(X\)に対して（いまは２次元なので\(X=\mathbf{R}^2\)で考えます）、

\begin{align*} \mathrm{UConf}_n(X):=\left(X^n\setminus \Delta\right)/{S_n} \end{align*}

ただし、\(\Delta :=\{(x_1, x_2,\cdots, x_n)\in X^n\mid x_i\neq x_j ( i\neq j)\}\)となる集合です。このような空間\(\mathrm{UConf}_n(X)\)を\(X\)の配置空間といい、その基本群\(\pi_1(\mathrm{UConf}_n(X))\)を組み紐群と言います。なんだかわけわかんないですよね。わからないを大切にしましょう（笑）

しかしながら、こういった配置空間というのはロボット工学などでも応用されています。例えば、自動化された工場におけるロボットがロボット同士ぶつからないように配置を移動するプログラムを設計する際にも使われます。

さて、話を戻します。今回の２パターンの席移動、単純な紐の図にすると以下のようになります。

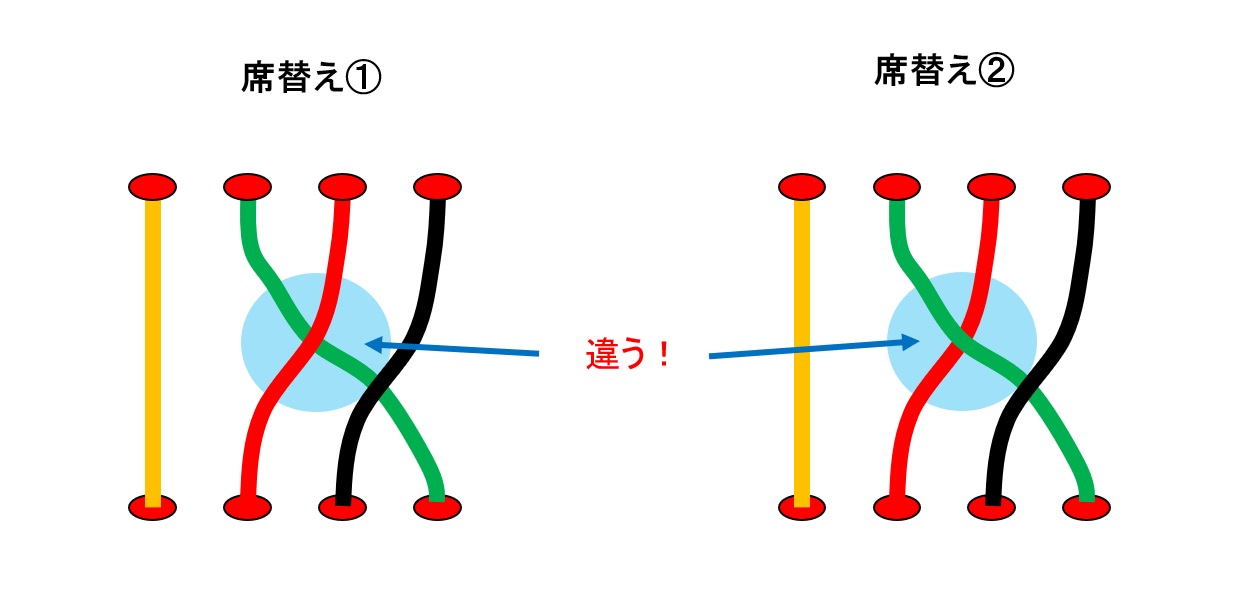
こうしてみると、緑の紐が赤の下にあるか上にあるか違いがあることがわかります。このように、時間変化込みの席の移動は「組み紐」と言われる数学的対象で捉えることができます。数学って素敵ですね！（感嘆符）

３．周期的な動きと考える

さらにここから、席の移動を「周期的な動き」ととらえましょう。周期的とはその動きが繰り返されるということ、つまりは「ループ」になるというイメージです。例えば２人の移動をループ化するというのは２人の軌道（紐）の上と下を結びつけることに対応します。こうすることで閉じた紐（結び目）が得られます。特に下の図のような結び目のことを「三葉結び目」といい、非常に有名な結び目です。

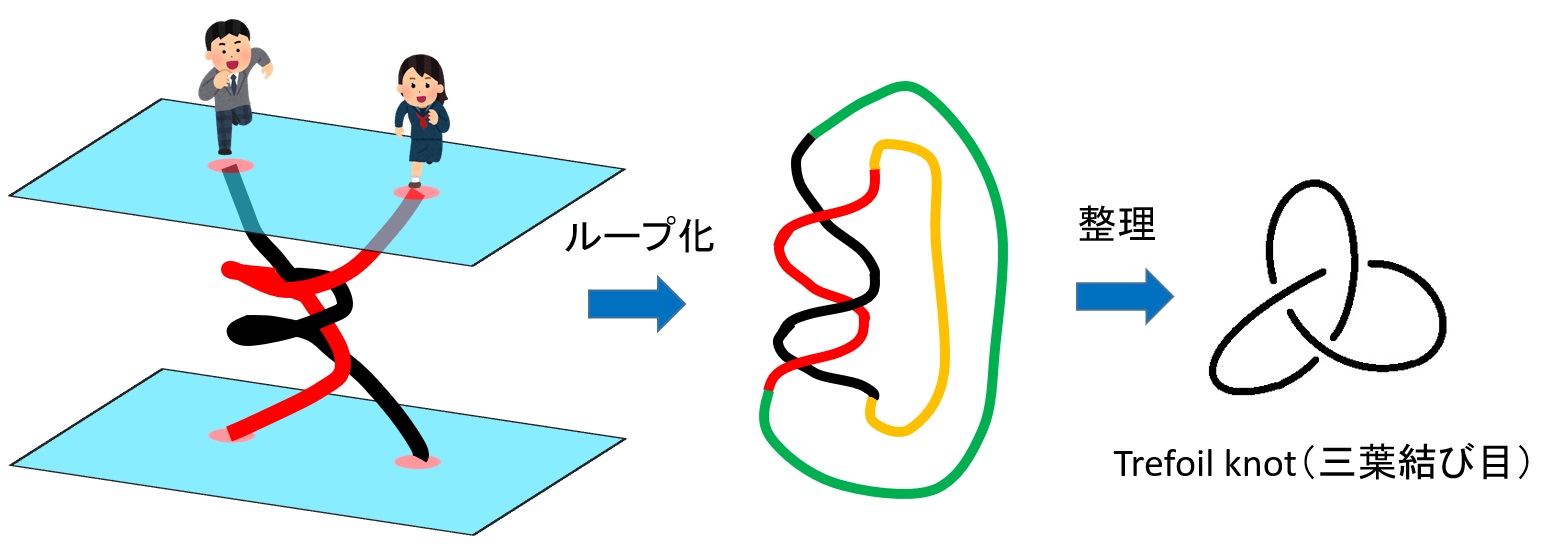
このような閉じた紐が１本の場合を「結び目（knot）」、複数の場合を「絡み目（link）」といいます。さて、いよいよ最後の考察です。

４．Perfumeへの応用

準備は整いました。ここで次のような問題を考えましょう。

Perfume配置変化問題

非常に気になる未解決問題です。今回は某テレビ番組出演時の「レーザービーム」という曲を披露した際の３人の動きについて考察しました。まず、３人の始まりと終わりの配置はがこちら。（※あ：あ～ちゃん、の：のっち、か：かしゆか）

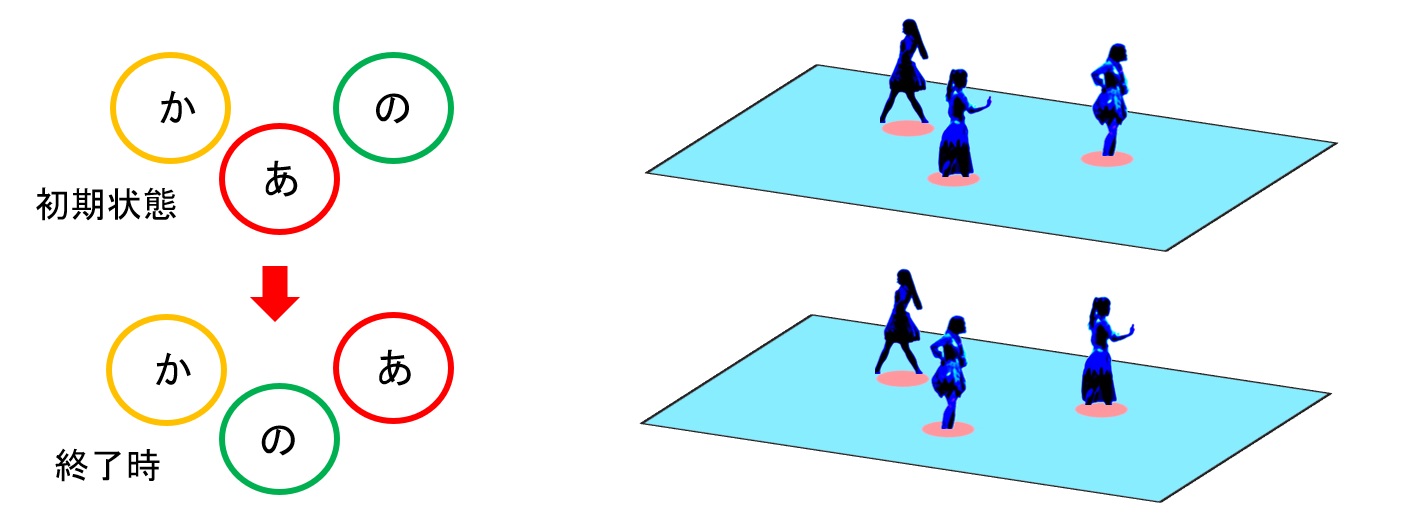
これだけ見ると結果的にはあ～ちゃんとのっちが入れ替わっているだけです。しかし、これは席替えではありません。その経過が大事なのです！さあ約４分のダンス、非常に複雑な動きもありましたが、配置に関しては意外とシンプル！

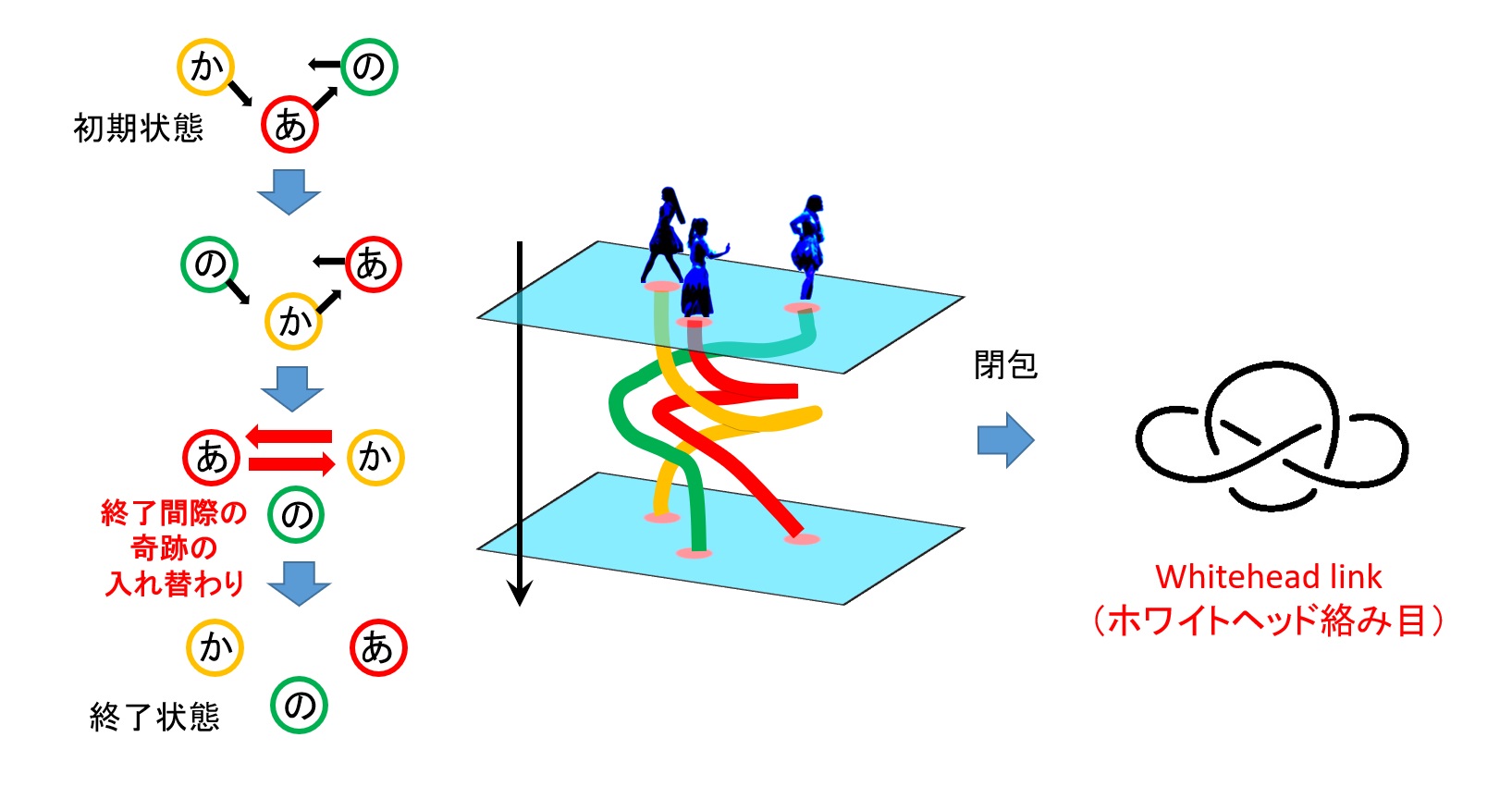
途中までは２回シフトだけだったのですが、終了間際に突如あ～ちゃんとかしゆかが入れ替わりました。この入れ替わりのおかげて実はループ（閉包）を考えたときの輪っか（絡み目）に、非常に豊富な数学的構造が入りました。。。！まさに奇跡です（軌跡だけに）。

さあ、出来上がった絡み目ですがなんと「ホワイトヘッド・リンク」と名前がついており、由緒正しい双曲絡み目の１種です。こんな数学的な構造が隠されていたんですね！

鳥肌が立ちました！ちょうど漫画「魔法陣グルグル」でキタキタおやじのお尻の動きから魔人ベームベームの召喚魔方陣が現れたときと似たような衝撃にちかいです（共感できる方いらっしゃいますか？）。

 

５．まとめと展望

今回のまとめと展望です。

・Perfumeのレーザービームには「ホワイトヘッド・リンク」が隠されていた。

・AKB48や３代目J SOUL BROTHERSで同様の考察をするとどうなるか。

AKBや３代目については他の人に譲ることにいたします。根気のある方は是非考察してみてください。なお、今回少し触れた「結び目」に関しては、それだけで一つの理論になっており「結び目理論（Knot Theory）」と言われています。結び目理論は視覚的な面白さがあり、非常に人気な研究分野の１つです。書籍としては「結び目理論とその応用　村杉邦夫（日本評論社）」がおすすめです。基礎的な内容から応用まで幅広くまとまってあります。

いかがでしたでしょうか。またロマンティック数学ナイトで講演する機会があればマスログに紹介していこうと思います。

なお、本記事をロマンティック数学ナイトで講演した際の実際のプレゼンの様子をYouTubeでも公開しています！是非ご視聴ください！

<文/岡本健太郎>