ピタゴラスの定理を使った美しい数学的デザイン!
公開日
2021年5月24日
更新日
2025年9月17日

こんにちは。和からの数学講師の岡本です。今回は、先日私個人のTwitterで予想以上に反響があった数学的デザインについてお話していきます。
ピタゴラスの定理により、各色の面積はずっと同じです。 pic.twitter.com/GY2RueVXcG
— ζWalker (@walker0226) May 15, 2021
中学校で習う、「ピタゴラスの定理(三平方の定理)」がカギとなるデザインになっていますが、想像もつかないですよね。早速みていきましょう!
この記事の主な内容
1.ピタゴラス・ツリー
まずはこちらをご覧ください。

カラフルで綺麗ですよね!これは通称「ピタゴラス・ツリー」と呼ばれており、数学的な構造が含まれています。純粋に見ているだけも楽しめますが、数学を知っているがどうかで、多様な捉え方ができるようになります。なお、「ピタゴラス」というのは古代ギリシャの数学者の名前であり、「ピタゴラスの定理」で有名です。実際に「ピタゴラス・ツリー」の由来にもなっています。
2.同じ構造が続く「自己相似図形」
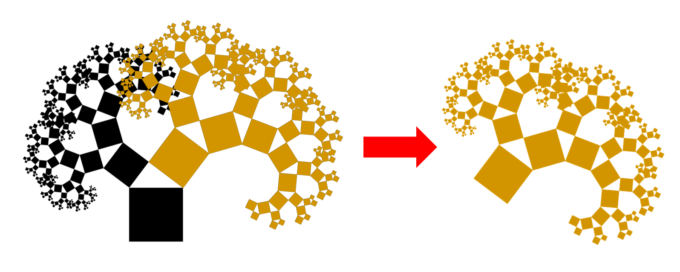
まず、見てすぐに分かるように、同じような構造が繰り返されることで図形ができています。よく見てみると、一部の形が全体の形に似ています。これは“自分自身に似た構造を持つ図形”とということで「自己相似図形」と言われます(厳密な定義はありますが、ここではカジュアルにお話します)。
実際に木の枝の構造と非常によく似ています。例えば、常に2本に枝分かれする木があったとします。枝分かれの際の開き具合(なす角)にはばらつきがあるかもしれませんがおよそ同じ開きからであるとしましょう。すると以下のような成長が予想されます。
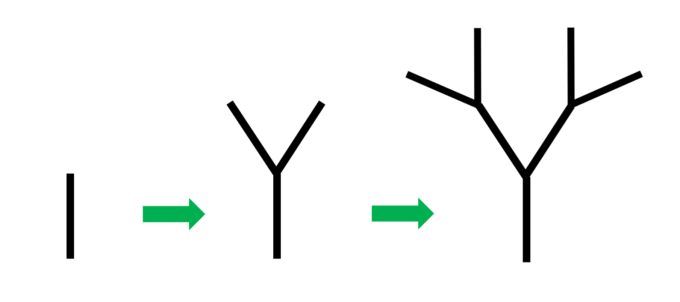
ピタゴラス・ツリーは簡単にいうと上のような構造が繰り返されることで描かれます。
3.ピタゴラスの定理とピタゴラス・ツリー
では次に「ピタゴラスの定理」との関係を説明していきましょう。
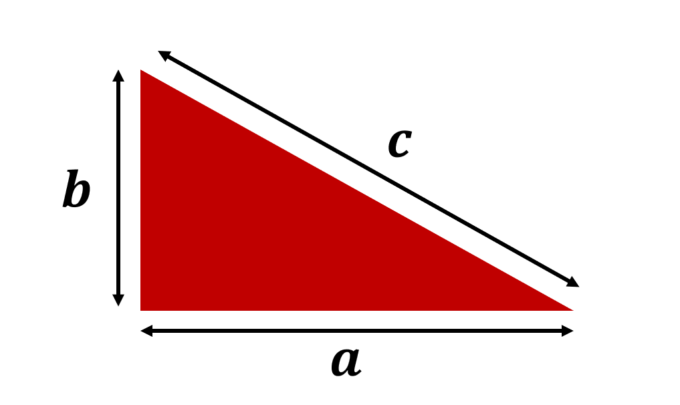
まず「ピタゴラスの定理」とは、上にような直角三角形の一番長い辺(斜辺)を\(c\)、残りの辺の長さを\(a,b\)とすると、次のような等式が常に成り立つと、というものです。
\begin{align*}
a^2+b^2=c^2
\end{align*}
3つの平方にまつわる定理であることから「三平方の定理」とも言われています。ピタゴラスの定理についてより詳しく知りたい方は過去のマスログにまとめてありますので、是非ご覧ください。
さて、この定理の意味を考えてみましょう。長さの2乗とは、その辺の長さを一辺とする正方形の面積と考えることができます。
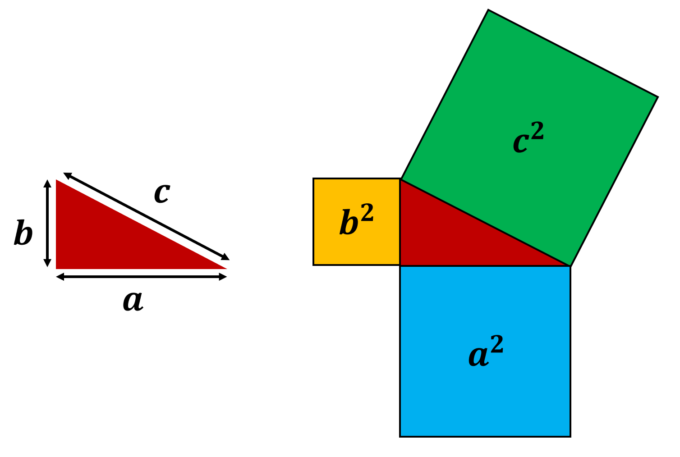
つまり、上の図のように、ピタゴラスの定理は「青の面積と黄色の面積の総和は緑の面積に等しい」と捉えることができます。これを踏まえると以下の図の下の正方形と上2つの正方形の面積の和は等しいことがわかります。
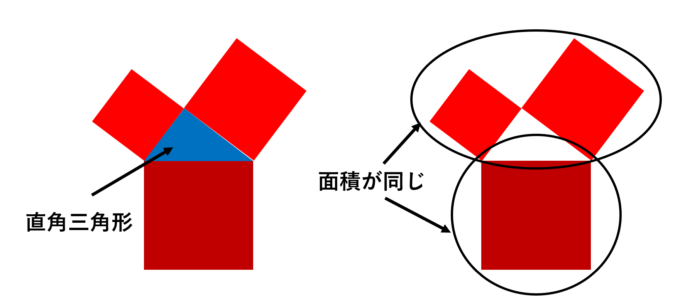
さらに小さな正方形(黄色)も、それぞれ赤の正方形と同じ面積になるはずなので、黄色の面積の合計は始まり正方形と同じであることがわかります。
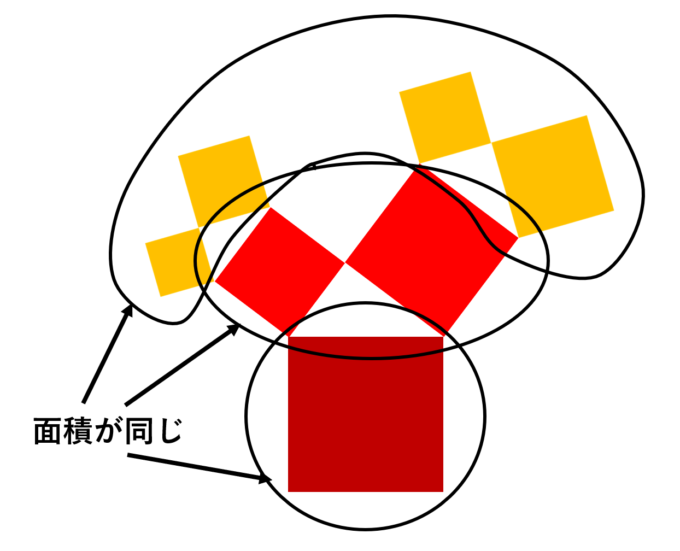
つまり、最初にお見せしたカラフルなピタゴラス・ツリーは「各色の面積が全て等しい」ということがわかります。(注1:当然重なる部分はあるので。見える範囲ではなく、重なった部分の色も加味します。注2:「各色」と言ってますが、もちろん背景の色(白色)は別です。)

色が10色なので、面積は土台の正方形10個分と同じであることがわかります!なんだか不思議ですね!

こうした数学的な構造が見えてくると、より一層美しさが増してきますね!まさに数学的なアートです!
4.さいごに
今回はPowerPointを使ったデザインを行いました。このようなExcelやPowerPointという、比較的身近なソフトを工夫して使うことで、綺麗な、また不思議な図形を描くこともできます!和からではこのような数学的デザインに関するセミナーを行っております!興味のある方は是非無料セミナーへご参加ください!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>
















