はじめに：分散の“平方根”が見える化のカギ

「データの散らばりとは？」シリーズ第2回では、前回の「分散」をさらに直感的にした指標、標準偏差（ひょうじゅんへんさ）を解説します。統計学の中でもビジネスで最も役立つのがこの標準偏差です。聞いたことはあっても「なんとなく難しそう」と感じる人が多いのではないでしょうか？でも大丈夫です。数式を覚えなくても、“平均からのズレ”という感覚さえつかめば理解できます。

---

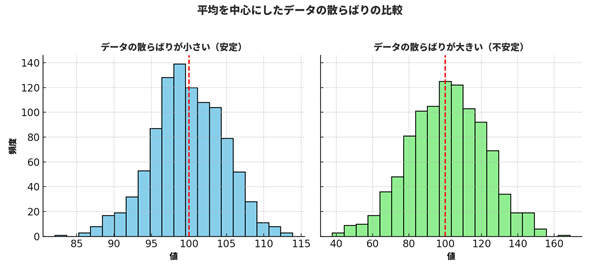
標準偏差とは：データのズレ幅を“元の単位”で表す

前回紹介した「分散」は、データのズレの二乗を平均したものでした。たとえば売上額のズレを二乗して平均した結果が200（万円²）になると、「平方単位」のためピンとこないですよね。

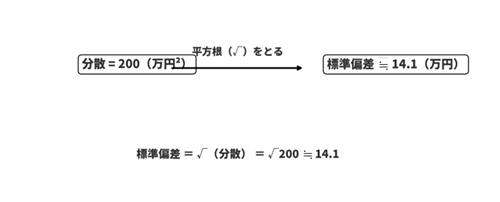
そこで平方根（ルート）をとって、元の単位（この場合は万円）に戻したものが標準偏差です。

標準偏差 ＝ √（分散）

つまり、分散が200なら標準偏差はおよそ14.1万円（＝√200）。これで「平均から14万円ほどズレている」と、具体的な感覚で把握できます。

---

標準偏差が教えてくれること

■ 値が小さい → データが平均の近くに集まっている（安定している）

■ 値が大きい → データが平均から大きく離れている（バラつきが大きい）

たとえば営業チームの月間売上の標準偏差が次のような場合を比べてみましょう：

・チームA：標準偏差 8万円 → 安定している

・チームB：標準偏差 25万円 → 結果がばらつく

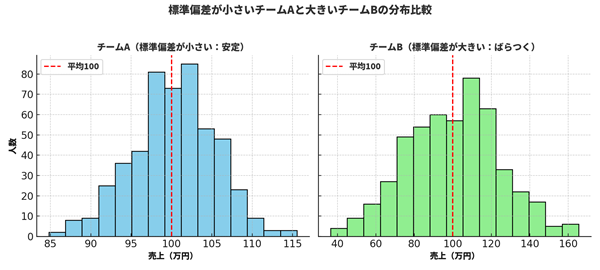
このように、標準偏差を見るだけで「どれくらい安定しているか」が数値で判断できます。平均値だけでは見えなかった“データの信頼性”が浮かび上がるのです。

---

標準偏差の読み方：±1σの範囲

標準偏差（σ：シグマ）は、データの多くがどの範囲に含まれるかを推測するのにも使えます。特に「正規分布（せいきぶんぷ）」という左右対称の分布では、次のような特徴があります：

■ ±1σ（平均±1標準偏差）に、全体の約68％のデータが入る

■ ±2σ（平均±2標準偏差）に、約95％のデータが入る

■ ±3σ（平均±3標準偏差）に、約99.7％のデータが入る

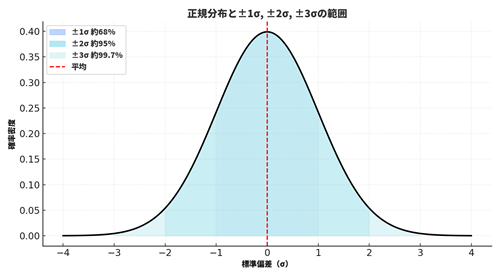
たとえば平均売上が100万円、標準偏差が10万円なら、だいたいの売上は 90〜110万円 に集中している（約68％）と考えられます。つまり、「±1σの範囲」は“だいたいの目安”を表してくれる便利な指標です。

---

ビジネスで使うときの例

標準偏差は一見理系っぽい指標ですが、実はビジネスのあらゆる場面で役立ちます。

売上管理

複数店舗の売上が平均100万円でも、標準偏差が小さい店舗群ほど“安定したビジネスモデル”。逆にバラつきが大きければ、店舗ごとにノウハウ格差があるかもしれません。

顧客満足度調査

平均点が高くても標準偏差が大きいなら、「好き嫌いが分かれる」商品。評価が安定しているかどうかを見るのに最適。

マーケティングKPI

広告のクリック率やコンバージョン率の標準偏差を追うことで、ターゲティングの一貫性やキャンペーンの再現性が把握できます。

---

付記：なぜ標準偏差は「σ（シグマ）」で表すの？

標準偏差はギリシャ文字の σ（シグマ） で表されます。これは、統計学で「合計」を意味する記号 Σ（大文字シグマ） に由来しています。分散や標準偏差を求める過程では「各データの偏差を合計する（sum）」という操作があり、その“合計”を象徴するシグマが使われています。

つまり：

■ Σ（大文字） → 合計を表す（数式中で使用）

■ σ（小文字） → 合計から導かれる“ズレの平均”（標準偏差）を表す

このように、σは「データ全体の広がりを要約した記号」として選ばれており、統計学で長く使われている伝統的な表記です。

---

まとめ：標準偏差は“安定性のモノサシ”

標準偏差は、平均値の“信頼度”を補う重要な指標です。分散では直感的に分かりにくかった「バラつきの大きさ」を、元の単位に戻して理解しやすくしたものです。

平均だけを見て安心していたデータも、標準偏差を併せて見ることで「どのくらい安定しているのか」「結果にムラがないか」を読み取れるようになります。

次回（第3回）は、分布の形そのものに注目して「データのかたより（歪み）」を読み解いていきましょう。

<文/綱島佑介>