「この紐、ほどける？」-結び目理論への誘い-

ロマンティック

公開日

2020年11月29日

更新日

2020年11月29日

こんにちは。和からの数学講師の岡本です。今回は比較的新しい数学の研究分野である「結び目理論」について簡単にお話しようと思います。個人的にも大好きな理論です。
早速ですが、次の問題を考えてみましょう。

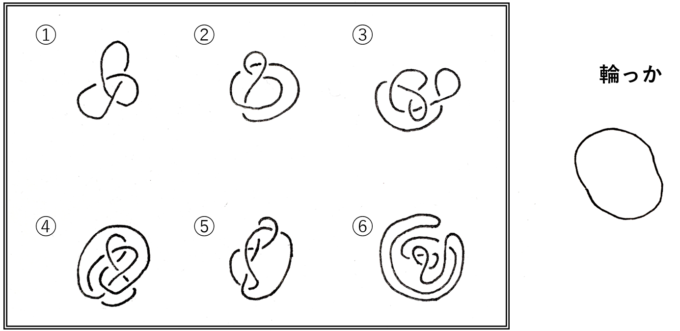
【問題】絡まった紐をほどくことで、単純な「輪っか」となるものを全て選んでください。

意外と難しく、頭のいい運動になります。(解答は本ページに下に表記しています)

この記事の主な内容

１．結び目とは？

「結び目」と聞くと紐と紐を結んで「つなげる」イメージがありますが、数学の研究対象としての「結び目」は、絡まって閉じている（＝輪として完結している）紐（「閉曲線」といいます）を指します。

２．結び目理論の問題

このような「結び目」は複雑に絡まっているように見えて、実はほどくと簡単な結び目であったり、想定していた結び目と「異なる」ものであったり、「結び目が同じかどうかの判定」は非常に難しい問題です。
例えば、実際にほどいてみて同じ形にできるのであれば、「同じである」と判断できますが、「同じでない」ことの証明は難しいのです！

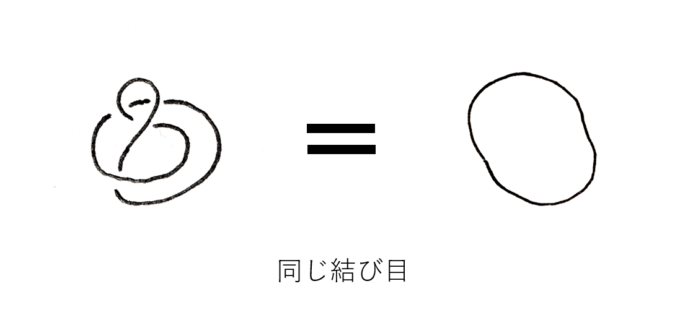
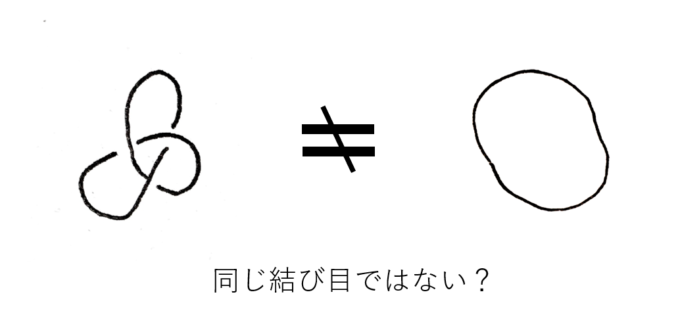
たとえば、一見して次の結び目はこれ以上ほどけず、輪にはならない、つまり、右の結び目と左の結び目は「同じでない」ように思えますが、「証明」となると難しくなってきます。ここで「結び目理論」の出番となります！

３．結び目理論の威力

結び目理論を使った結び目の判定方法として「多項式」や「数値」を使った古典的な方法があります。
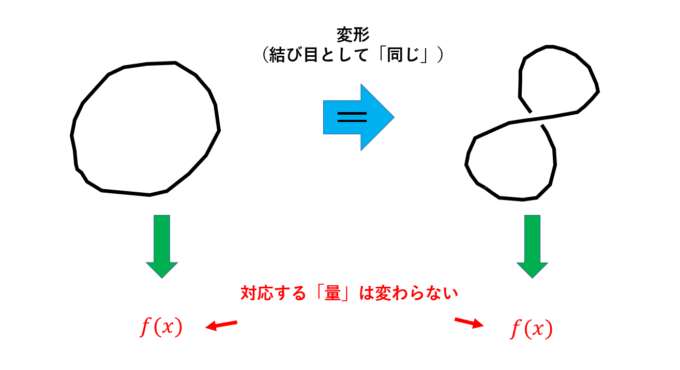
つまり、結び目の絡まり具合の情報から多項式や数値といった「量」を対応させ、２つの「量」が「異なる」ものであれば、元の結び目も「異なる」ものであることが証明できます！

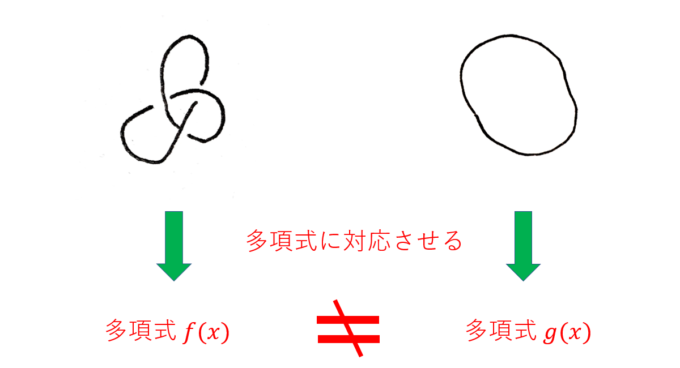
ただし、どんな「量」でもいいわけではありません。例えば、結び目を少しねじったもの（連続的に変形したもの）と最初の結び目とで、対応する「量」が違ってしまうといけません。結び目にはいくつかの基本的な「変形（ライデマイスター変形）」があり、これらの変形に対し「変わらない量」があれば便利です。このような「変わらない量」のことを総じて「不変量」と呼びます。有名な不変量としてAlexander多項式、Jones多項式、HOMFLY多項式、最小交点数、橋指数など、大量にあります。

４．さいごに

近年では、これらの不変量をまとめる理論や生物学（DNA関係）、化学（原子の結合構造）への応用など、様々な発展が見られます。また、結び目はデザインとしても最近では注目されており、ファッションデザイナーのエマ理永さんによる、結び目をモチーフにしたドレスというものもあります。美しいですね！
https://www.emarie-weddingdress.com/works_and_philosophy/topology_topological_form.html

さらに、岡本デザインの結び目マグカップも好評発売中です！