こんにちは。和からの西原です。
講師として、算数や中学数学の学び直しを担当しています。

前回は「文字を使った式」について、「なぜ文字を使う必要があるのか？」と「使い方」を紹介しました。
今回は式を立てる際、出来るだけシンプルに考えるうえで、大事な「関係性」について触れていきたいと思います。

文字を使った式 (歴史編) – 中学数学初級編 –

天秤のバランスで考える「等しい」の意味

今回は「シンプルに考える」ことの一つの例として、天秤を使って左右のおもりのバランスを考えることに着目したいと思います。

【チェックポイント】

(1). 左右の重さが同じ時、天秤は水平になります。
※この時「左辺(左側)」と「右辺(右側)」は同じ重さ(等しい)という関係がわかります。
(2.) 「左辺」と「右辺」が同じ重さの時、左辺と右辺の間に「=(イコール)…等しい」記号を使うことで両辺(左辺と右辺両方)同じ重さであると表すことができます。

それでは下の図をみていきましょう。
※天秤のバランスに着目してみてください。

図1： AとBのおもりは同じ重さです。

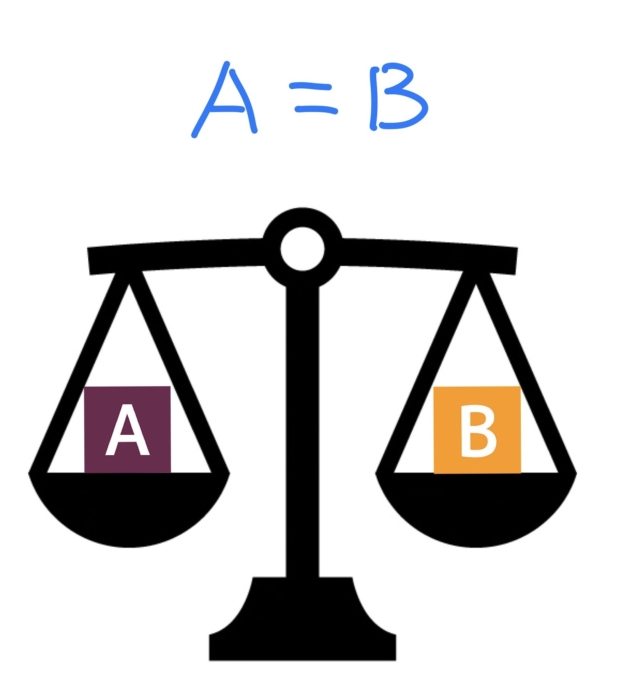
図2： AとB両方におもりCを加えても重さは同じです。

図3： AとB両方からおもりCを除いても重さは同じです。

図4： AとB両方のおもりを2倍にしても重さは同じです。

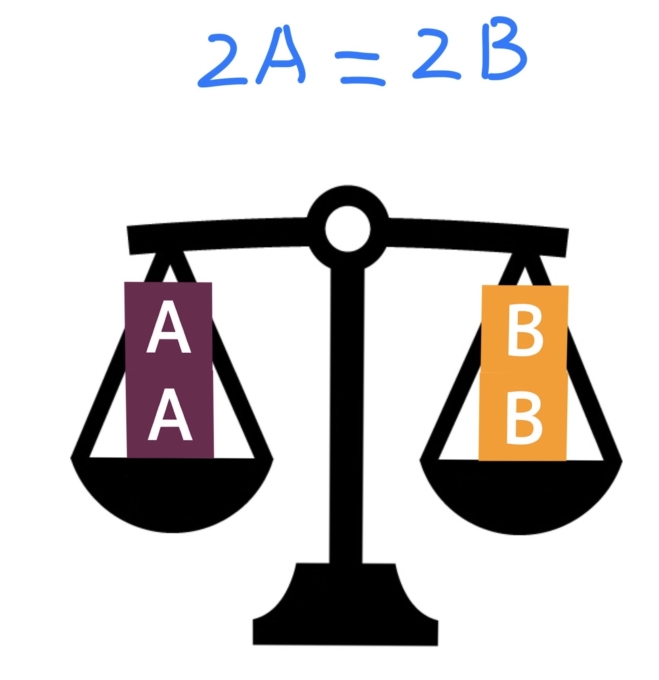
図5： Aのおもりは2倍、Bおもりを3倍にしたとき重さは同じではありません。
※バランスは崩れてしまいます。

図6：AとB両方のおもりを半分の重さにしても重さは同じです。
半分にする… ÷2することは1/2倍すると同じことでした。


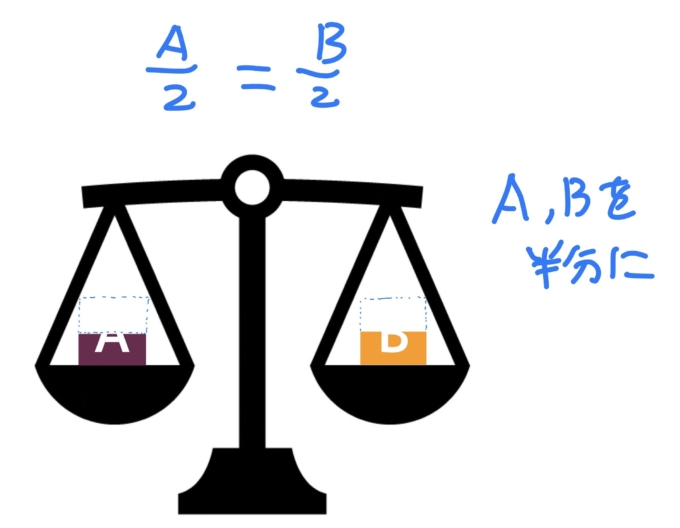
最初の重さが同じであれば両辺に同じことをしてもバランスは崩れません。しかし、違うことをした時にはバランスは崩れてしまいます。

おわりに

今回は天秤を使ったバランスから、最初の重さが同じ時、両辺に同じことをしてもバランスは崩れない。(等しい関係)であるということを確認しました。
次回は、この性質を使って「左辺(左側)の数や文字を右辺(右側)に移す(本当に移すなのか?)」について紹介したいと思います。