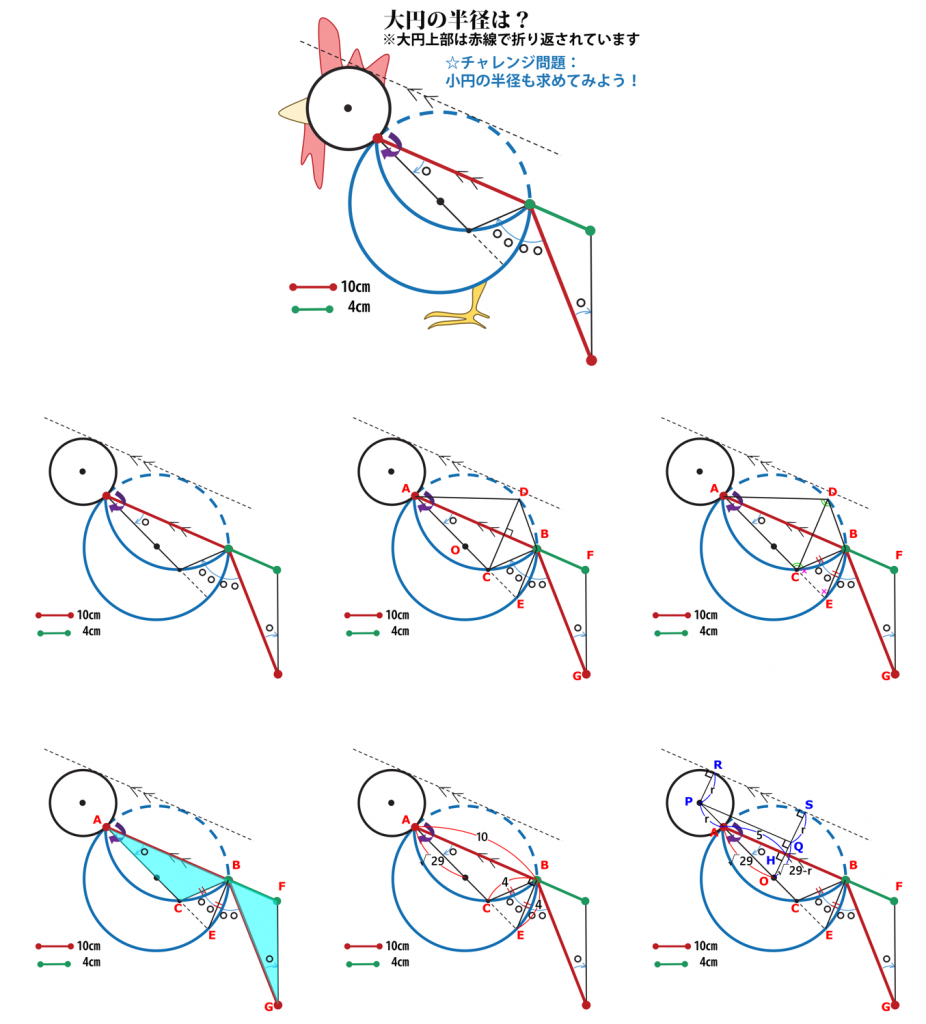
【2017年】年賀状問題解答発表!
公開日
2017年1月20日
更新日
2017年1月20日
毎年恒例【年賀状問題】の発表日です。
今年の年賀状問題はいかがでしたでしょうか。
例年よりも【やや難】という声が多かったのですが、
今年も多数の解答の応募をいただきました。
解答を送ってくださった皆様ありがとうございます!
惜しくも解答にたどり着かなかった皆様、
以下に解答を掲載いたしますので、
「再チャレンジしたい!」という方はここで一旦ストップして下さいね。
解答を読まれる方は、
問題を印刷したものに書き込みながら読まれると理解しやすいかと思います。
それではいよいよ発表です!
ここに気付けば解ける!問題の急所
解答詳細の前に、まずは「ここに気付けば解ける!」という、
最大のPOINTを記載します。
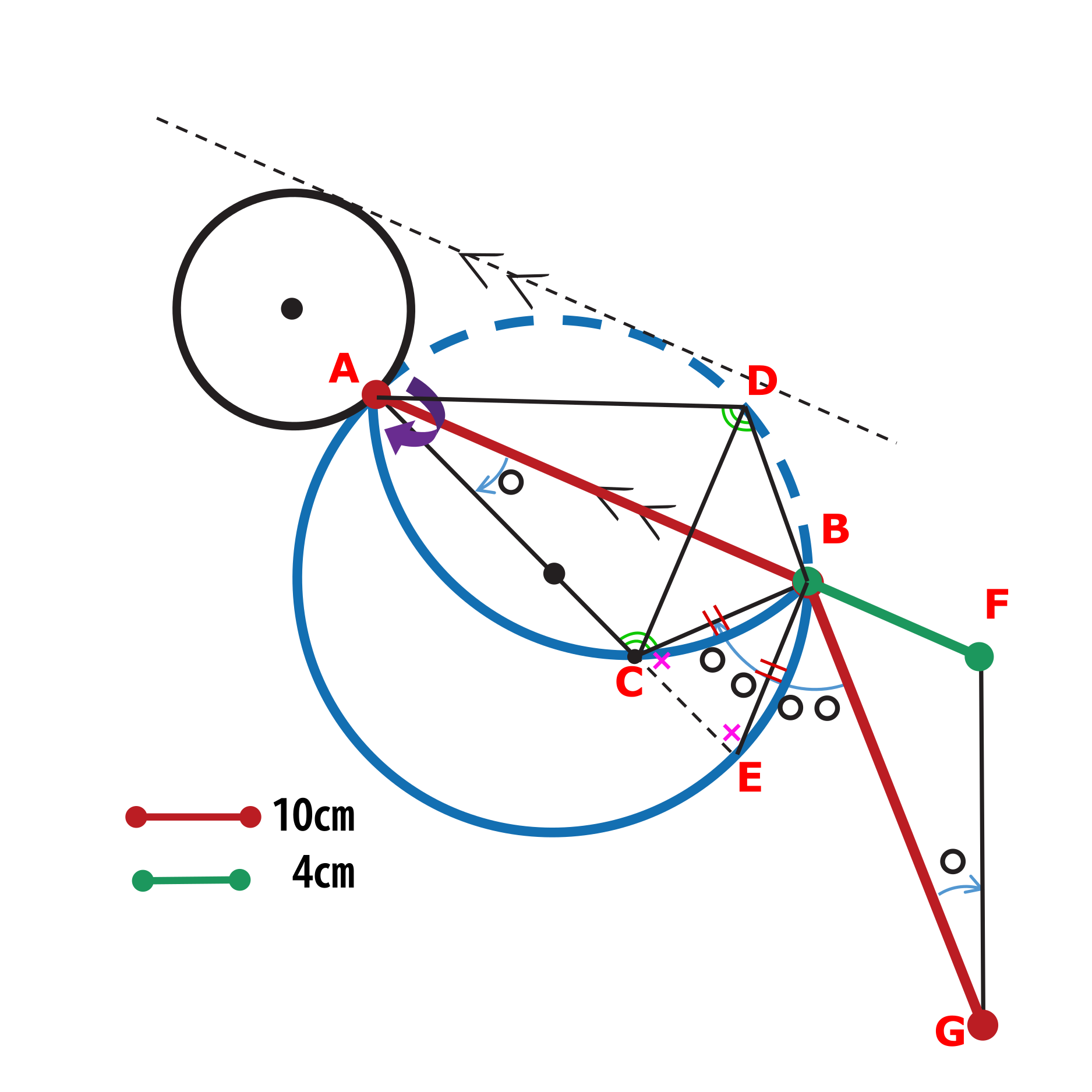
本問では以下の図のように、
①△CBEが二等辺三角形であると気づくこと
②また、①を利用して△BCA≡△BFGであると気づくこと
の2点が急所でした。
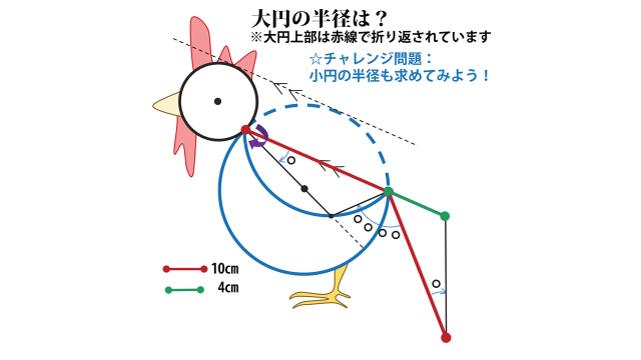
さあ、それでは解説です!
STEP①
まずは下図のように頂点に名前を付けます。
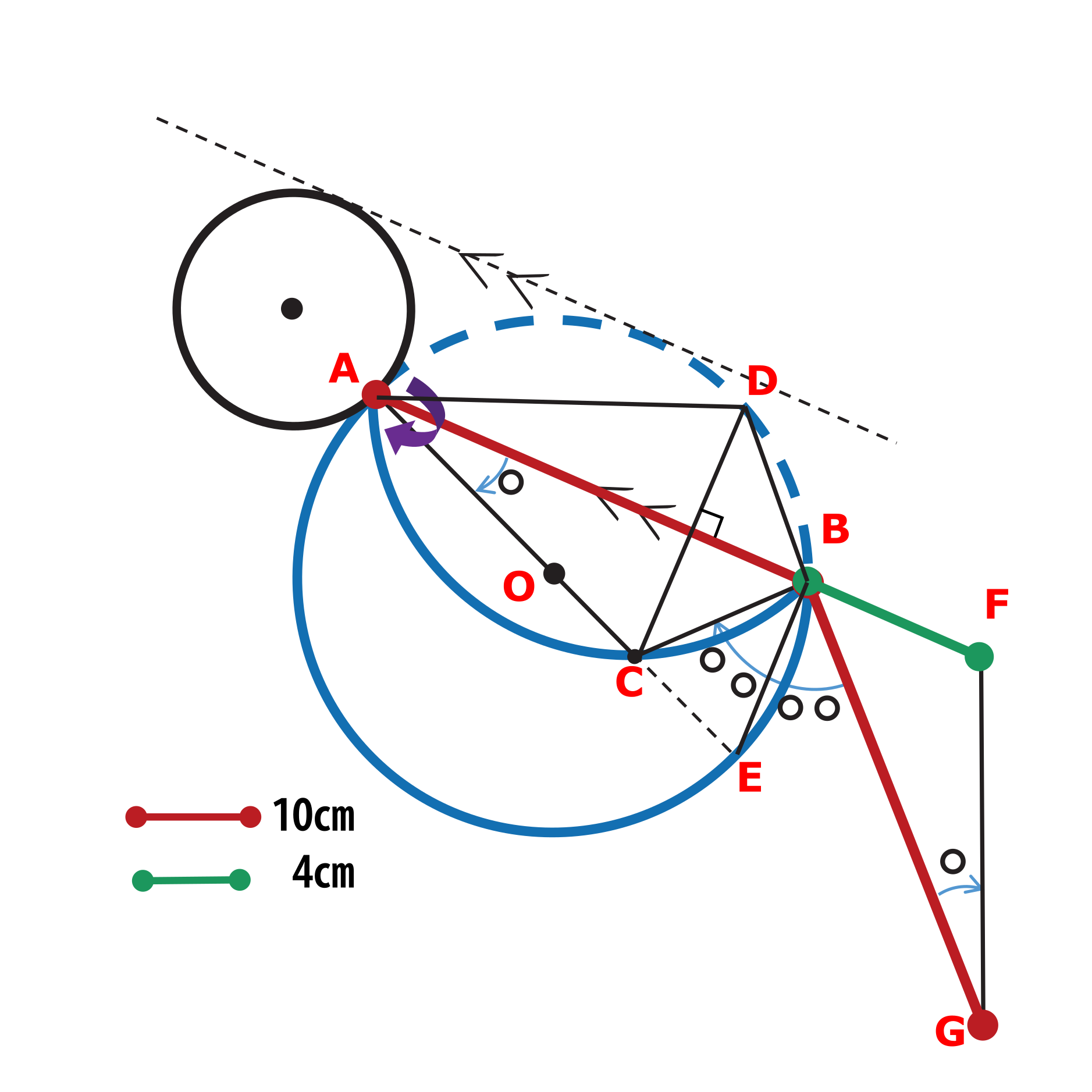
DはCをABについて折り返す前の大円上の点です。
すると、折り返しなので
∠ACB=∠ADB …★
□ADBEは円に内接する四角形なので向き合う角度の和が180°となるため、
∠BEC=180°-∠ADB
★(∠ACB=∠ADB)を利用すると
∠BCE = 180°-∠ACB = 180°-∠ADB = ∠BEC ,
∠BCE=∠BEC から △CBEは二等辺三角形であるので
BC = BE.
これで急所が1つ突破できました。
STEP②
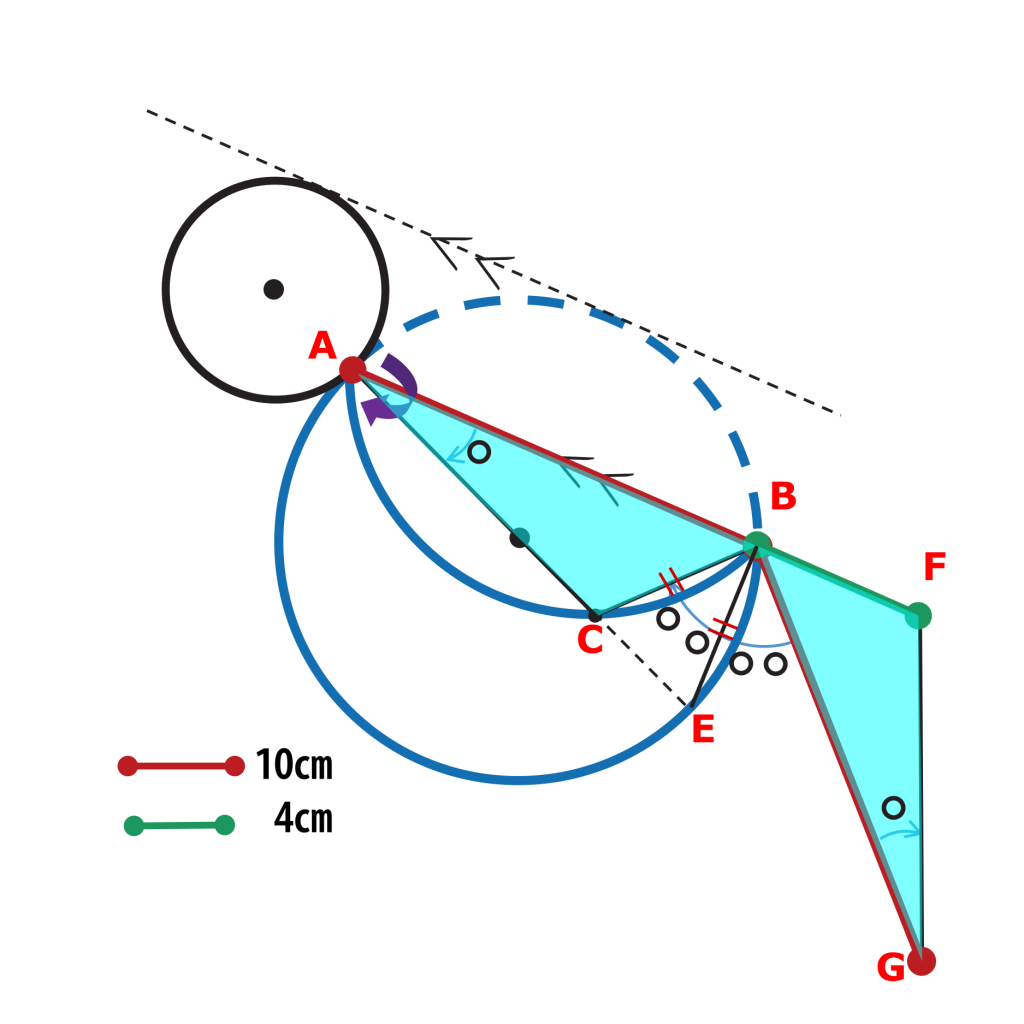
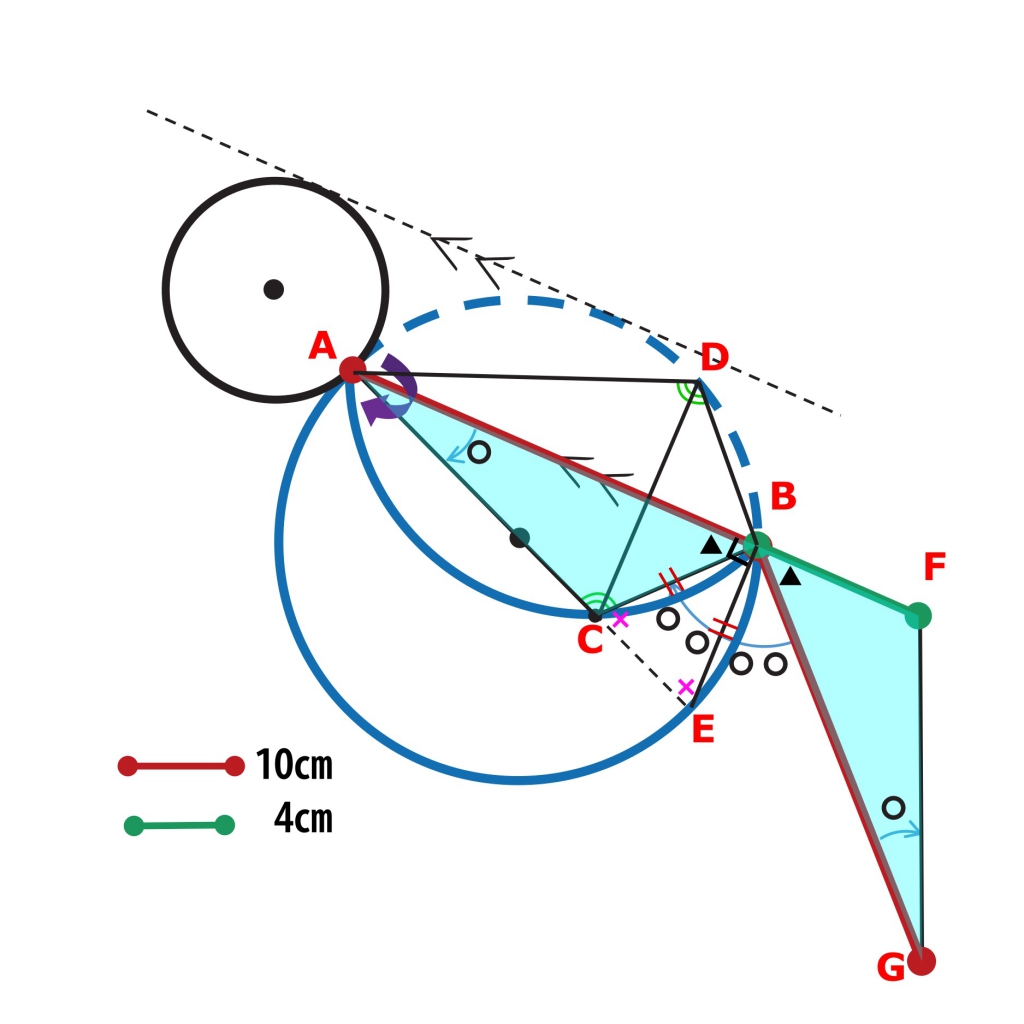
次に急所の2点目である△BCA≡△BFGを示します。
まず円周角の定理より、
∠ABE = 90° なので
△ABEに注目して
∠BAE(○)+∠BEA(×) = 90°
したがって
(○○)+(××)=180° .(○2つ分と×2つ分の角度の合計が180°)
これより、
∠CBE=(○○) かつ ∠EBG=(○○)
なので
∠ABC(◢) = 90°-∠CBE = 90°-(○○) = ∠GBF(◢),
よって△BCAと△BFGについて一辺とその両端の角がそれぞれ等しいので
△BCA≡△BFG.
これで急所の2点目も突破です。
あとは求めたい解答まで一直線です!
STEP③
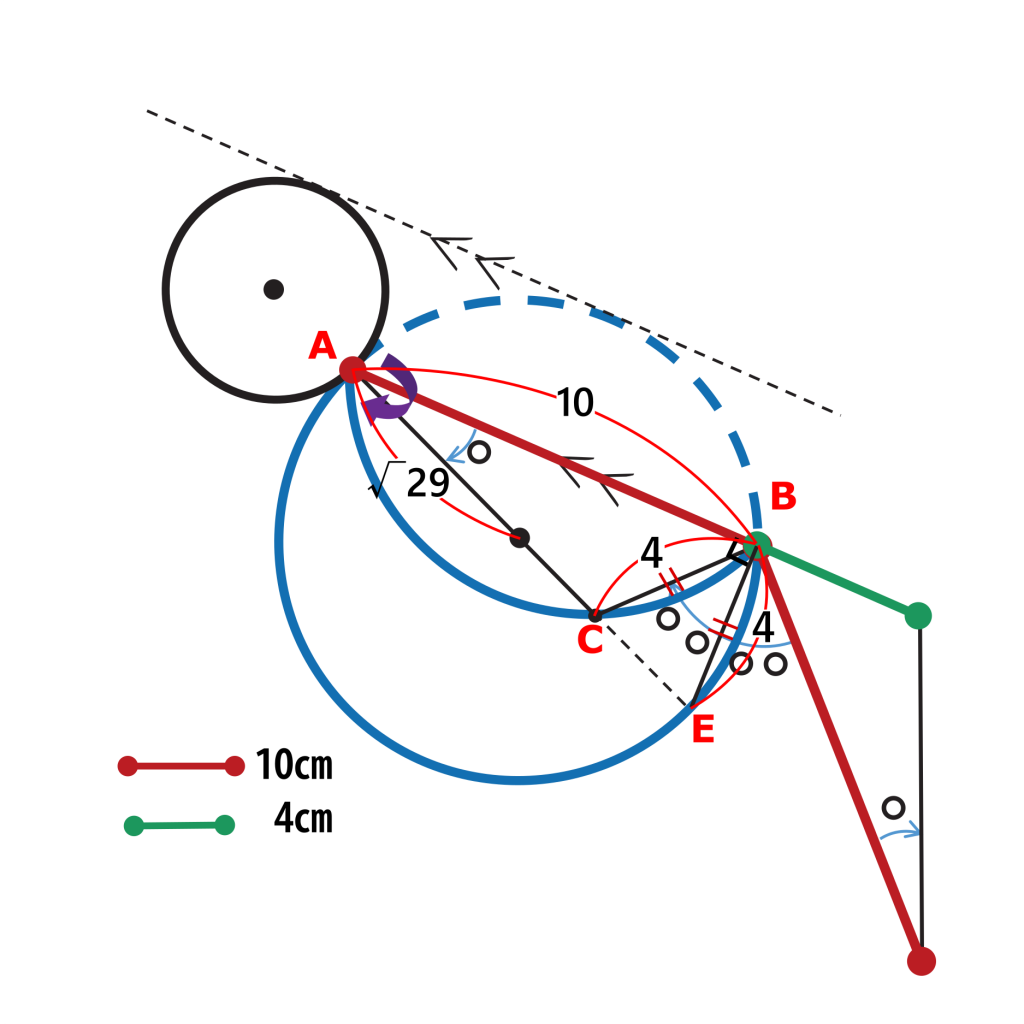
以上の結果より△ABEは
AB=10cm
BE=BC=BF=4cm
の直角三角形である。
そこで三平方の定理より、大円の半径は
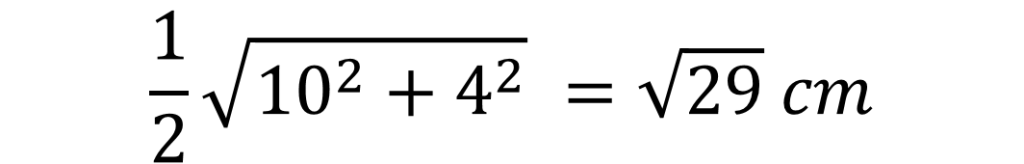
となります。
お疲れ様でした。
これで問題はクリアです!
ここからは【チャレンジ問題】の解説となります。
STEP④
下図のようにOAを延長すると、Aが大円と小円の接点なので小円の中心Pを通る。
また、P,Oから点線に垂線を下した足をR,Sとする。
さらに、PからOSに下した垂線の足をQ、OSとABの交点をH とする。
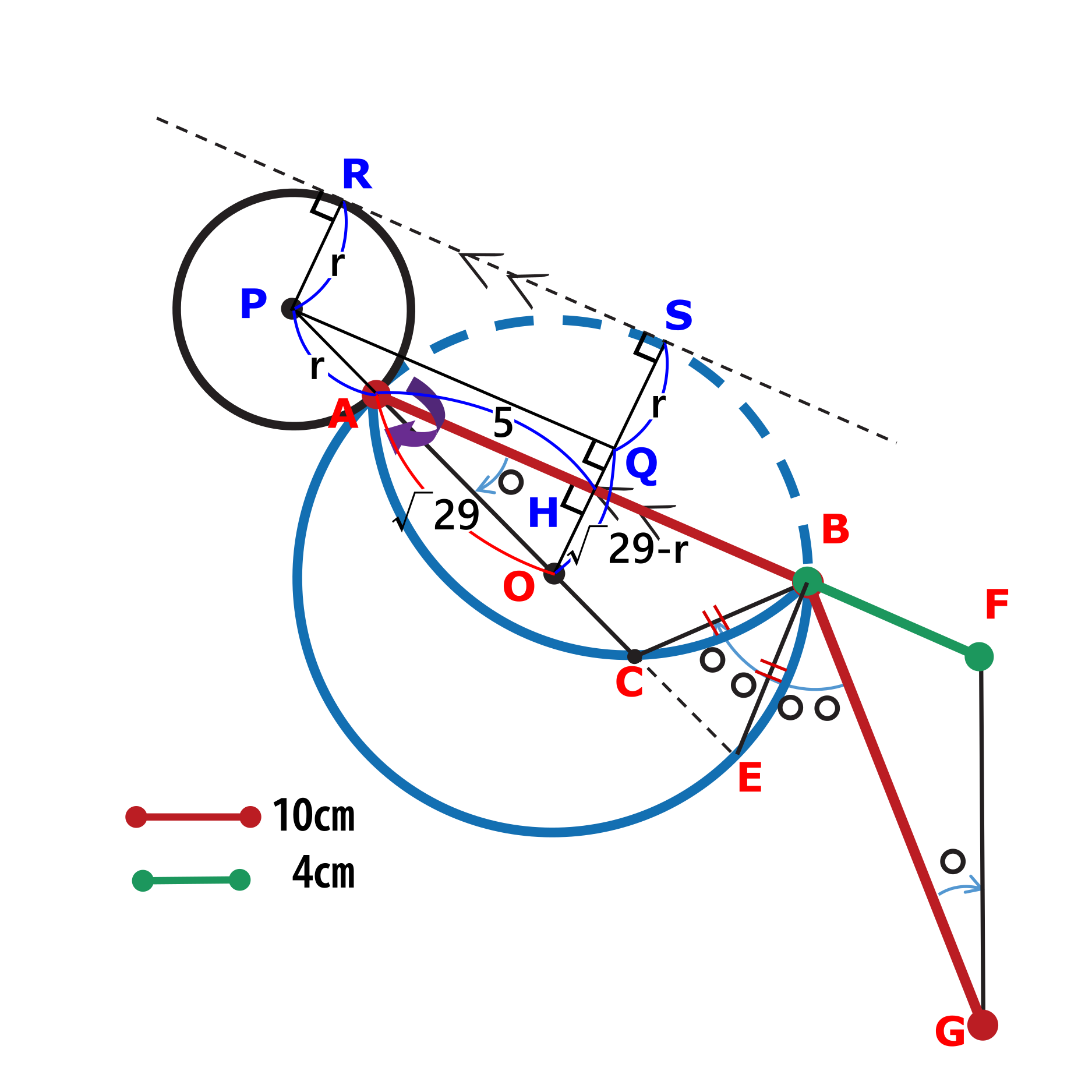
∠AHO=90°でありRS//PQ//AHなので
△AHO ∽ △ABE より
HO=2cm, AH=5cm
△PQO ∽ △AHO より
PO : QO = AO:HO
小円の半径をrとおくと、
PO=√29 + r
QO=√29 -r
なので、
PO : QO = √29 + r : √29 -r = √29:2 = AO:HO
これを解くと、小円の半径rは
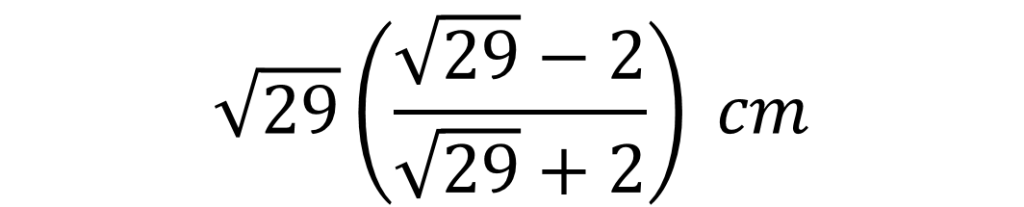
となります。
皆様いかがでしたか?
以下に解答のサマリーを掲載しますので、
あらためて流れをご確認ください。
それでは皆様、今年も楽しい数学ライフを満喫しましょう!!
解答サマリー