確率の考え方-第1回:偶然を“数で考える”最初の一歩【統計学をやさしく解説】
公開日
2025年10月22日
更新日
2025年12月2日

この記事の主な内容
はじめに(導入)
「商談が決まる確率」「新商品がヒットする確率」「プロジェクトが期日に収まる確率」——ビジネスの現場は、見えない“確率”に満ちています。直感や経験だけで判断すると、思わぬリスクやチャンスを見逃すことも。この記事では、こうした“偶然”を数で読み解き、意思決定に活かす最初のステップを紹介します。難しい数式は使わず、実務に即した例と図で“確率的思考”を自然に身につけましょう。
この記事でわかること
◆ 確率の基本:全体(起こりうる結果のすべて)と、起きてほしい結果の関係
◆ 樹形図:考え漏れを防ぎ、可能性を“見える化”する道具
◆ 直感とのズレ:誕生日のパラドックスなど、意外な確率
◆ Excelでの簡単可視化:明日からできる、確率の表・グラフ化
1. 確率とは?——「全体」と「その一部」を割合で捉える
確率は「起こりうるすべての結果(※全事象=考えられる全てのパターン)」のうち、「関心のある結果(※事象=注目している結果)」が占める割合です。
例:100枚のくじに“当たり”が5枚 → 当たりの確率は 5 ÷ 100 = 5%
例:明日の雨予報40% → 10日あれば平均して4日は雨、という“期待”の度合い
ポイント:確率は未来を“当てる”ためではなく、備えや行動を整えるために使います。
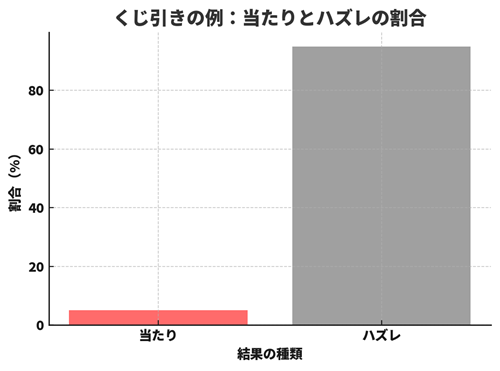
| 結果の種類 | 枚数 | 割合(%) |
|---|---|---|
| 当たり | 5 | 5% |
| ハズレ | 95 | 95% |
※割合は Excel で =枚数/合計 と入力し、セルを“パーセント表示”に設定すれば自動計算できます。
2. 樹形図で“可能性の全体像”を見える化する
頭の中だけで考えると、可能性の数を見落としてしまうことがあります。樹形図(じゅけいず)とは、結果を枝分かれで描くことで、「どんな結果があり得るか」をひと目で整理できる図です。まるで“思考の地図”のように、抜けや重複を防ぎ、考えを整理するのに役立ちます。
ポイント:樹形図は「全パターンを列挙する表」とは少し違います。全パターン表が“結果をリスト化”するのに対して、樹形図は“どうやってその結果に至るか”という順序や流れを視覚的に整理できるのが特徴です。
【図1】コイン2回の樹形図
スタート
│
┌───────┴───────┐
表(1回目) 裏(1回目)
│ │
┌───┴───┐ ┌───┴───┐
表(2回目) 裏(2回目) 表(2回目) 裏(2回目)
全事象4通り。「表表」は1通り ⇒ 25%
全事象4通り。「表表」は1通り ⇒ 25%
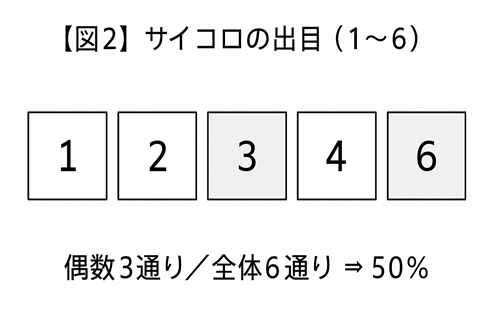
偶数3通り/全体6通り ⇒ 50%
3. 「おお!」と驚く直感とのズレ:誕生日のパラドックス
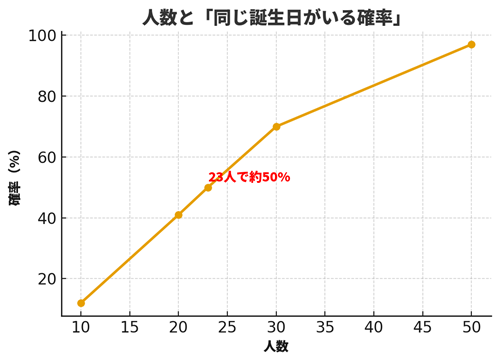
23人集まると、同じ誕生日の人がいる確率は50%を超えます。これを聞くと多くの人が「そんなに高いの?」と驚きます。直感では低く感じるのに、なぜそんな結果になるのでしょうか?
それは、人の数が増えると“比較の組み合わせ”が急激に増えるからです。23人いれば、1人ずつが他の22人と比較できるので、合計で約250通り以上のペアが生まれます。どれか1組でも誕生日が一致する確率を考えると、全体としては半分を超えるのです。
ビジネスへの示唆:偶然の一致(たまたまの相関)を“因果関係”と決めつけない。まずは全体像(母集団)と組み合わせ数を考える習慣を持つことが重要です。
| 人数 | 確率(%) |
|---|---|
| 10人 | 約12% |
| 20人 | 約41% |
| 23人 | 約50% |
| 30人 | 約70% |
| 50人 | 約97% |
※ざっくりの近似値でOK。人数が増えると、組み合わせが爆発的に増えるため確率が急上昇します。
4. Excelで今日からできる!確率のかんたん可視化
◆ 樹形図の代わりに、A列とB列で全パターンを列挙してみよう。
| 1回目の結果(A) | 2回目の結果(B) | 組み合わせ(A×B) |
|---|---|---|
| 表 | 表 | 表表 |
| 表 | 裏 | 表裏 |
| 裏 | 表 | 裏表 |
| 裏 | 裏 | 裏裏 |
※この表は Excel の列A(1回目)と列B(2回目)に「表/裏」を入力し、
組み合わせ列を =A2&B2 と入力すると自動で作成できます。
◆ くじの当たり枚数を変えて確率の変化を棒グラフで確認しよう。
| 当たり枚数 | 確率(%) |
|---|---|
| 5 | 5% |
| 10 | 10% |
| 20 | 20% |
| 30 | 30% |
| 50 | 50% |
※当たり枚数を増やすと確率はほぼ直線的に上昇します。
Excelで「当たり枚数(横軸)」「確率(縦軸)」をグラフ化すると、この関係が一目でわかります。
当たり枚数 → 5 10 20 30 50
確率(%) → ▓▓ ▓▓▓▓ ▓▓▓▓▓▓▓▓ ▓▓▓▓▓▓▓▓▓▓ ██████████████
5% 10% 20% 30% 50%
当たり枚数が増えると確率は比例的(直線的)に上昇することがわかります。
5. まとめと次回予告:確率は“未来を当てる”より“備えるため”の考え方
確率は「結果を予言する魔法」ではなく、より良い判断を下すための“道しるべ”です。偶然を数で捉えることで、直感に流されずにリスクやチャンスを見極められるようになります。
◆ 確率は「どのくらい起こりそうか」を示す冷静な判断の定規
◆ 樹形図は「考え漏れを防ぐ」ための思考整理ツール
◆ 誕生日のパラドックスは「人の直感はしばしば間違う」ことを教えてくれる
明日からできる確率思考の3ステップ
1. 「全体」と「一部」を数で整理する
2. Excelなどで“可視化”して確率を体感する
3. 結果より“しくみ”を見る——偶然を因果と混同しない
次回:
「確率の考え方-第2回:同時確率と独立のルールをやさしく理解する【統計学をやさしく解説】」では、営業成約率や再購入率など、社会人に直結する実例を使って確率の掛け算をわかりやすく解説します。














