はじめに：平均が同じでも“安定性”は違う

統計学をやさしく解説するシリーズ「データの散らばりとは？」。今回の第1回は、データの広がりを示す「範囲」と「分散」について解説します。平均を見て「どのチームが優れているか」を判断することは多いですが、平均が同じでも結果の安定性がまったく違うことがあります。これを見抜くのが「データの散らばり」です。

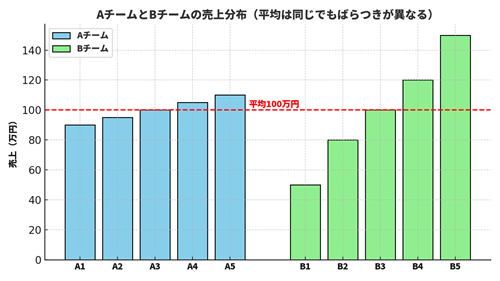
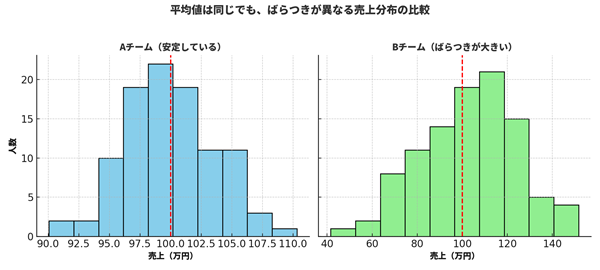
たとえば、営業チームAとBの平均売上がどちらも100万円だったとします。しかし、Aチームはメンバー全員が90〜110万円の間に集中しているのに対し、Bチームは50万円から150万円までバラバラ。この場合、Aチームの方が「安定している」と言えます。この“ばらつき”の大きさを数値で表すのが「散らばりの指標」です。

---

範囲（レンジ）：もっともシンプルな散らばりの指標

「範囲（レンジ）」とは、データの最大値と最小値の差を取ったものです。計算はとても簡単で、

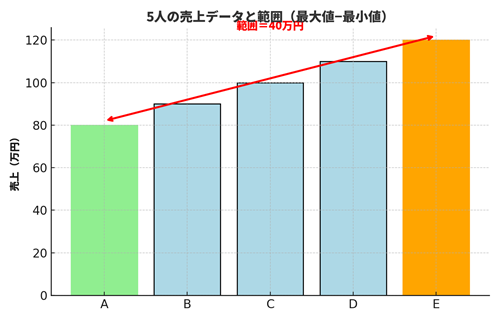
範囲 ＝ 最大値 − 最小値

たとえば、社員5人の売上が 80万円、90万円、100万円、110万円、120万円 の場合、最大値は120、最小値は80なので、範囲は 120 − 80 ＝ 40万円 です。これで「このデータは40万円の幅でばらついている」と分かります。

範囲の特徴と注意点

■ 計算が簡単で直感的に理解できる。

■ ただし、1つの極端な値（外れ値）に大きく影響される。

■ データが多い場合や偏りがある場合には、信頼しすぎない。

つまり、範囲は「データの広がりの目安」にはなりますが、安定性を正確に測るにはもう少し精密な方法が必要です。それが次に紹介する「分散」です。

---

分散とは：データが平均からどれだけズレているか

「分散（ぶんさん）」は、各データが平均からどのくらい離れているかを表す指標です。つまり、1人ひとりの結果が平均から“どの程度ズレているか”を数値化したものです。

たとえば、社員5人の売上が次のようだったとします：

社員	売上（万円）
A	80
B	90
C	100
D	110
E	120

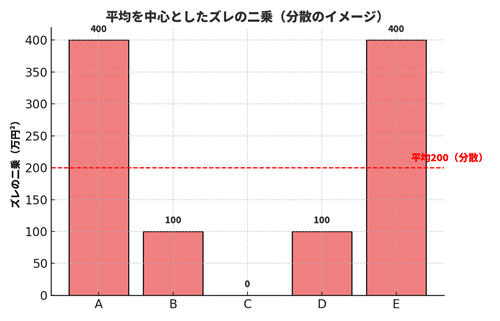
平均は100万円です。各人の「平均からのズレ（＝差）」は、-20, -10, 0, +10, +20 になります。

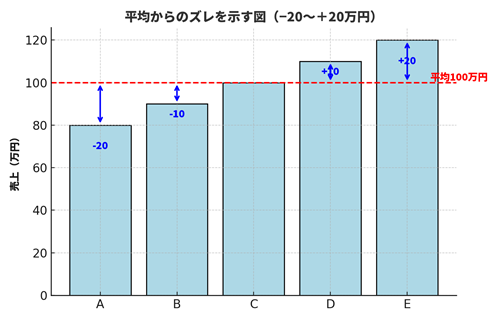
分散では、この「ズレ」を2乗して平均します。2乗するのは、プラスとマイナスを打ち消さずに“ズレの大きさ”だけを見るためです。

分散 ＝ （それぞれのデータ − 平均）² の平均

この例では、((-20)² + (-10)² + 0² + 10² + 20²) ÷ 5 ＝ (400 + 100 + 0 + 100 + 400) ÷ 5 ＝ 200

したがって、分散は「200（万円²）」です。この単位の“²（平方）”がポイントで、金額の平方という少し直感に合わない単位になります。この点を解決するのが次回紹介する「標準偏差」です。

分散のポイント

■ データのズレを正確に反映できる。

■ 外れ値の影響を受けやすい。

■ 単位が平方になる（例：万円²）。

---

ビジネスで使うときの「散らばり」感覚

ビジネスの現場では、「平均」だけで判断すると誤解が生まれることがあります。

■ 売上の安定性：平均は同じでも、バラつきが小さいチームの方が再現性が高い。

■ 顧客満足度アンケート：平均点が高くても、評価のバラつきが大きいと「好き嫌いが分かれる」商品。

■ 広告成果：クリック率の分散が小さいほど、ターゲティングが安定している。

---

まとめ：散らばりを見ると“データの性格”がわかる

範囲と分散は、どちらもデータの“ばらつき”を示す基本の指標です。範囲はシンプルで直感的、分散はより正確に“ズレの度合い”を数値化します。どちらも平均だけでは見えない「データの安定性」を教えてくれます。

次回は、この分散をさらにわかりやすくした「標準偏差」について解説します。平方の単位を取り除き、データの散らばりを“実感できる形”にする方法を学びましょう。

<文/綱島佑介>