連立方程式の考え方と解き方【算数からやさしく解説】
公開日
2022年9月10日
更新日
2025年9月17日
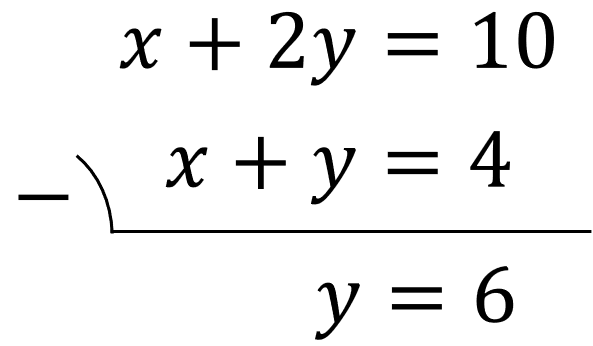
↓↓↓動画で見たい方はこちら↓↓↓
この記事の主な内容
連立方程式とは
連立方程式とは、複数の方程式の組み合わせです。中学数学では連立方程式の前に一次方程式の解き方を学びました。一次方程式では解くべき文字(\(x、y、a、b\)など)が一つであったのに対し、連立方程式では解くべき文字が複数あります。連立方程式は主に以下のように一次方程式が複数並んだ形になります。

では、連立方程式の解き方について\(2\)つの方法を学びましょう。この記事では、\(2\)つの式で構成される連立方程式の解き方について解説します。
加減法
加減法とは、\(2\)つの式を足したり引いたりして連立方程式を解く方法です。\(x\)と\(y\)の一次方程式を\(x\)のみ、\(y\)のみの一次方程式に直すことができれば、慣れ親しんだ一次方程式の問題に帰着させることができます。
最初は式を足したり引いたりしても良いのかと心配になるかもしれません。しかし、\(=\)の両辺は等しい値であるので、式を足し引きするということは同じ値を足し引きすることと変わりありません。具体例を用いて考えてみましょう。
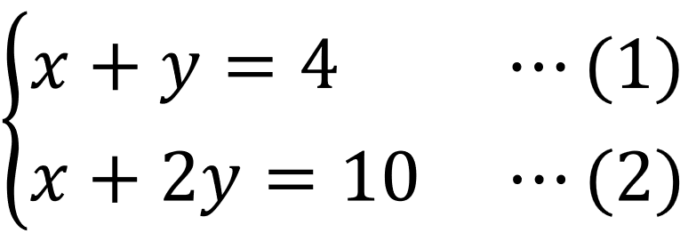
(1)と(2)を見てみると\(x\)の係数が両方\(1\)であることが分かります。そのため、(2)-(1)をすることによって、\(x\)の文字が消えます。
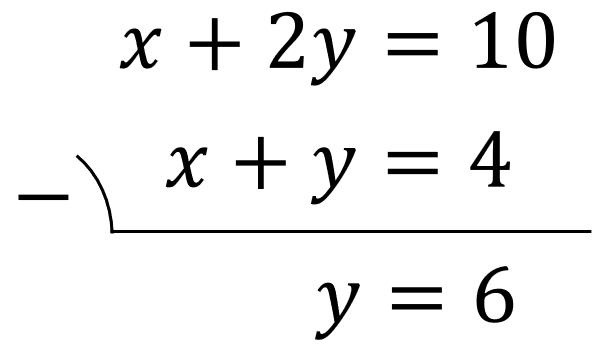
左辺は \(x+2y\) から \(x+y\) を引くので、\( (x+2y)-(x+y)=x+2y-x-y=y\) になります。
また、右辺は\(10\)から\(4\)を引くので、\(6\)になります。
式を引き算することによって、\(y\)のみの式(\(y=6\))を得ることができました。
\(y=6\) であるので、これを元の連立方程式のいずれかの式に代入してxの値を求めます。
\(x+y=4\) に \(y=6\) を代入すると
\(x+6=4\) となり、\(6\)を右辺に移動させることで \(x=4-6=-2\) と分かります。
よって、この連立方程式の解は \(x=-2\)、\(y=6\) です。
代入法
代入法とは、片方の式を\(”x=”\)、\(“y=”\)という風に変形してもう片方の式に代入する方法です。もう片方の式に代入することによって加減法と同様、\(x\)と\(y\)の一次方程式を\(x\)のみ、\(y\)のみの一次方程式に直すことができます。加減法で用いた例を代入法で解いてみましょう。
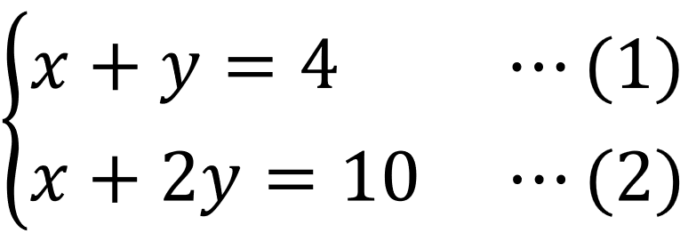
はじめに、\(”x=” \)もしくは\(”y=” \)の式を作りたいので、片方の式を変形します。今回は\(”x=” \)の式を作ってみましょう。(1)について、\(y\)を右辺に移項すると、\(x=4-y\)になります。
\(x=4-y\)という式が得られたので、次にこの式を(2)に代入します。
(2)の\(x\)を \(4-y\) に置き換えると、左辺は \(x+2y=(4-y)+2y=y+4\) になります。
これが\(10\)に等しいので、\(y+4=10\) を解き、\(y=10-4=6\) を得ます。
最後に、\(y\)の値を \(x=4-y\) に代入して\(x\)の値を求めると、\(x=4-y=4-6=-2\) になります。
よって、\(x=-2\)、\(y=6\)となります。これで、代入法と加減法のどちらの方法を用いても答えは変わらないということが確認できました。
まとめ
この記事では、連立方程式の意味とその\(2\)つの代表的な解法について確認しました。
連立方程式は数学でしか使わない考え方だと思われがちですが、実際には連立方程式の考え方は経済や経営の場面で頻繁に用いられます。例えば、マクロ経済で用いられるIS-LM曲線や経営で用いる損益分岐点分析は連立方程式の考え方を使用します。連立方程式を用いることで、複雑な問題からシンプルに結論を得ることができます。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/須藤>