↓↓↓動画で見たい方はこちら↓↓↓

相似な図形とは

相似な図形とは、ある図形を形を保ちながら拡大・縮小させた図形のことです。

上図のように相似な図形△ABCと△DEFがあるとき、数学の本などでは「∽」という記号を用いて「△ABC∽△DEF」という風に表します。これは「三角形ABC　”そうじ”　三角形DEF」と読みます。

また、似た概念として合同な図形といったものがありますが、相似と混同しないようにしましょう。合同な図形は長さ、角等が完全に同じ図形であるため、合同であれば相似となりますが、相似であっても必ずしも合同とはなりません。

三角形の相似条件

相似な図形を判別するための条件として、相似条件というものが存在します。四角形や楕円などについても相似条件は存在するのですが、今回は特に簡単で使われる機会の多い三角形の\(3\)つの相似条件について紹介します。

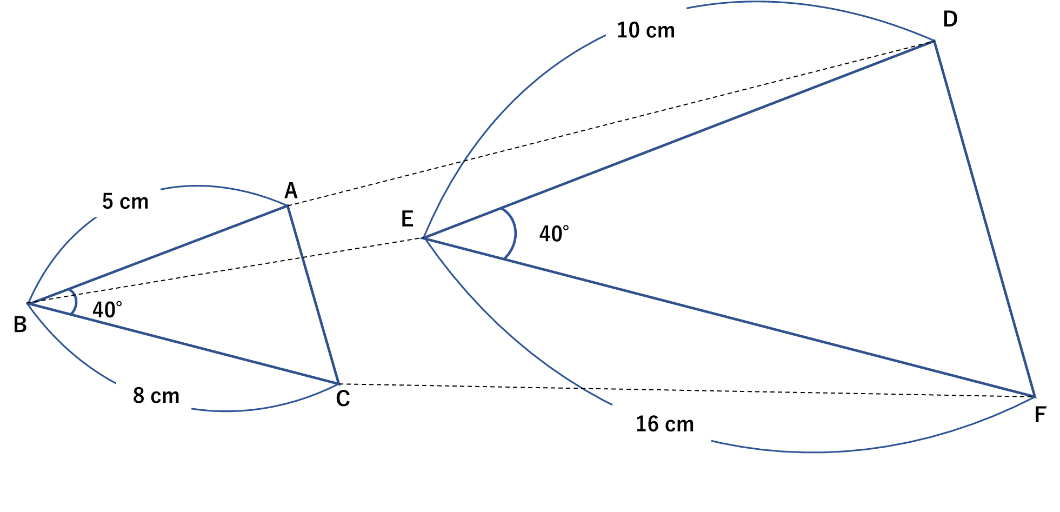
1. 全ての辺の比が等しい

この例では△ABCの辺の比が小さい順に\(3:5:8\)になります。△DEFの辺の比は小さい順に\(6:10:16=3:5:8\)となり、全ての辺の比が等しいと分かります。そのため、△ABC∽△DEF（相似）となります。

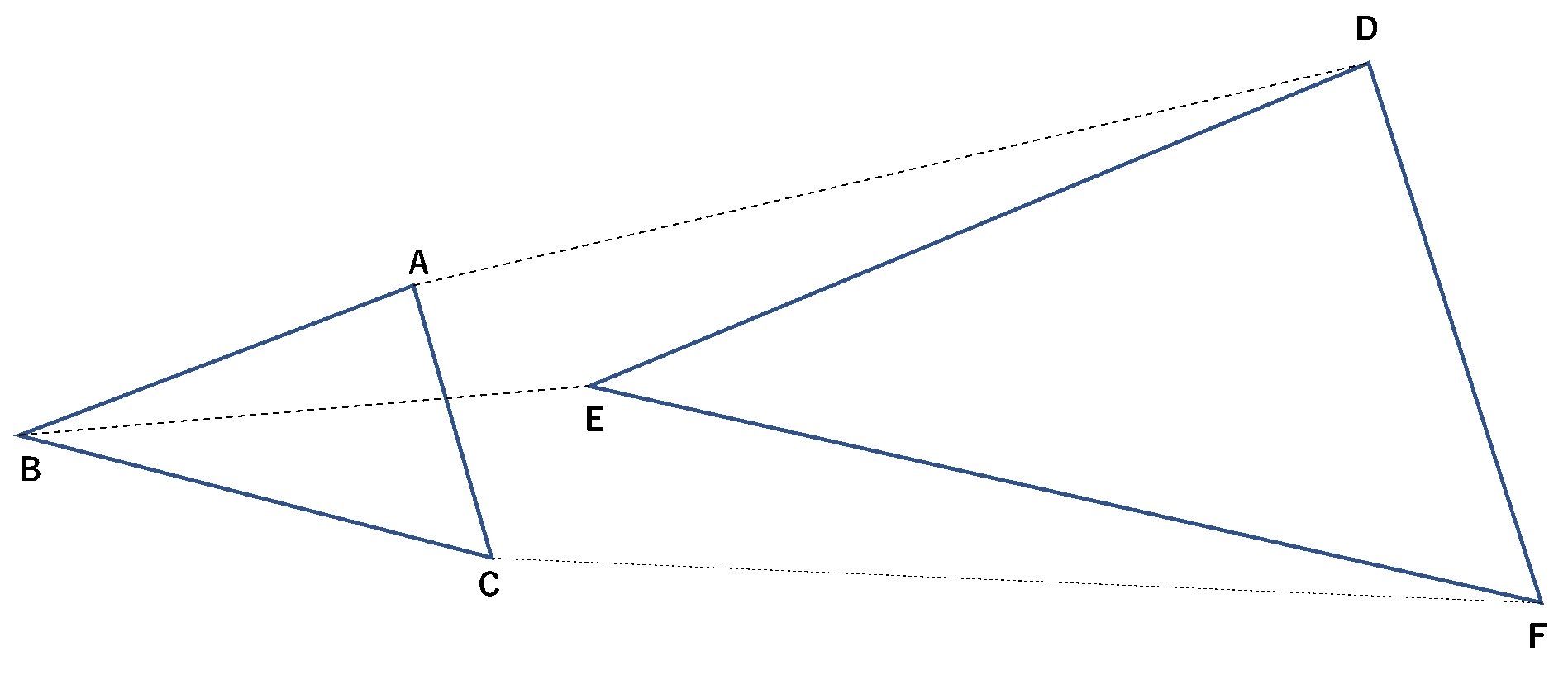
2. 全て（\(２\)つ）の角度が等しい

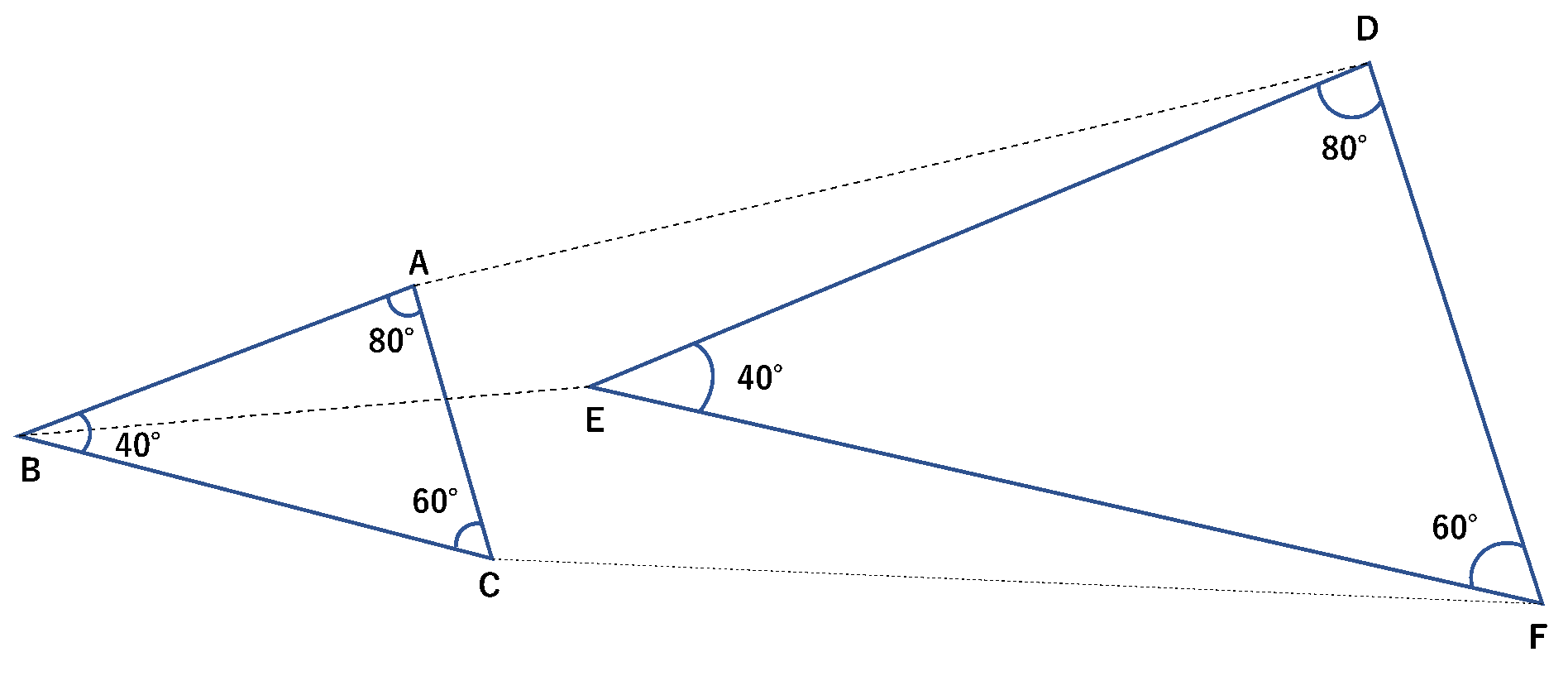
一つ目の条件は全ての辺の比に着目しましたが、全ての角に着目することによって相似が判断できます。角度は拡大・縮小しても変わらないため、角度が等しいとき、相似であると言えます。
また、「全て（\(2\)つ）」としているのは\(2\)つの角度が分かっていれば残り\(1\)つの角度についても求めることができるからです。三角形の角の和が\(180°\)であることを利用して、（残りの角）\(=180°-\)（\(2\)つの角の和）という風に計算できます。
⇒例: \(40°\)と\(80°\)が分かっている場合は（残りの角）\(=180°-(40°+80°)=60°\)

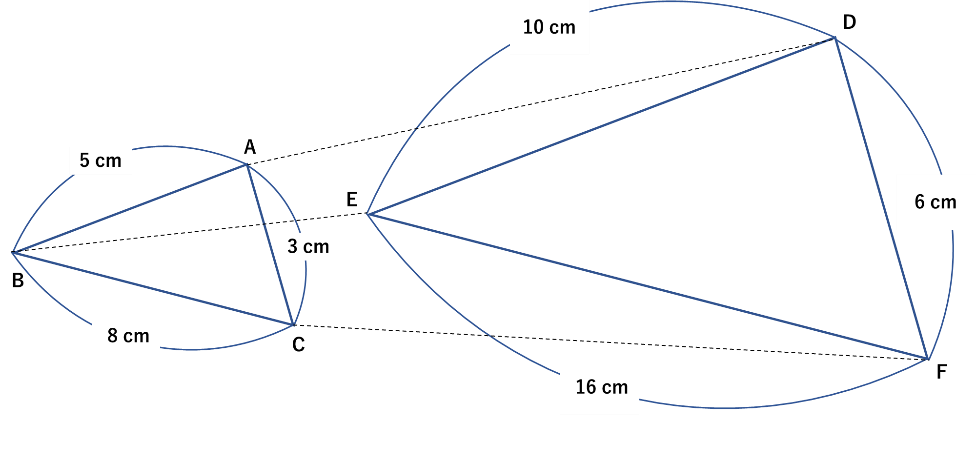
3. \(2\)辺の比とその間の角が等しい

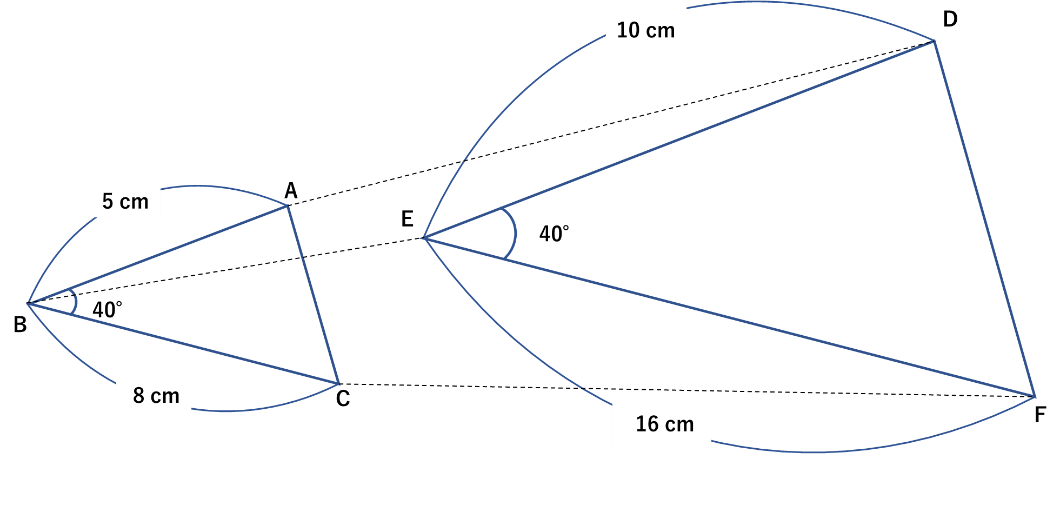
最後に、三角形の\(2\)辺の比とその\(2\)辺の間の角が等しい場合に相似と判断できます。上図の場合、\(2\)辺の比は\(5:8=10:16\)となり、その間の角も共に\(40°\)なので、相似であると判断します。

これらの\(3\)つの条件のいずれかが満たされるとき、\(2\)つの図形が相似だと判断することができます。

相似比とは

相似比とは、相似な図形の対応する辺の長さの比のことを言います。つまり、図形を何倍拡大もしくは縮小することによって\(2\)つの図形が一致するか、を示す比です。相似比を求めることによって、面積比や不明な長さを求めることができるため、相似比が利用されることが多いです。

相似比を求めることによって、二つの図形の面積比を求めることができます。

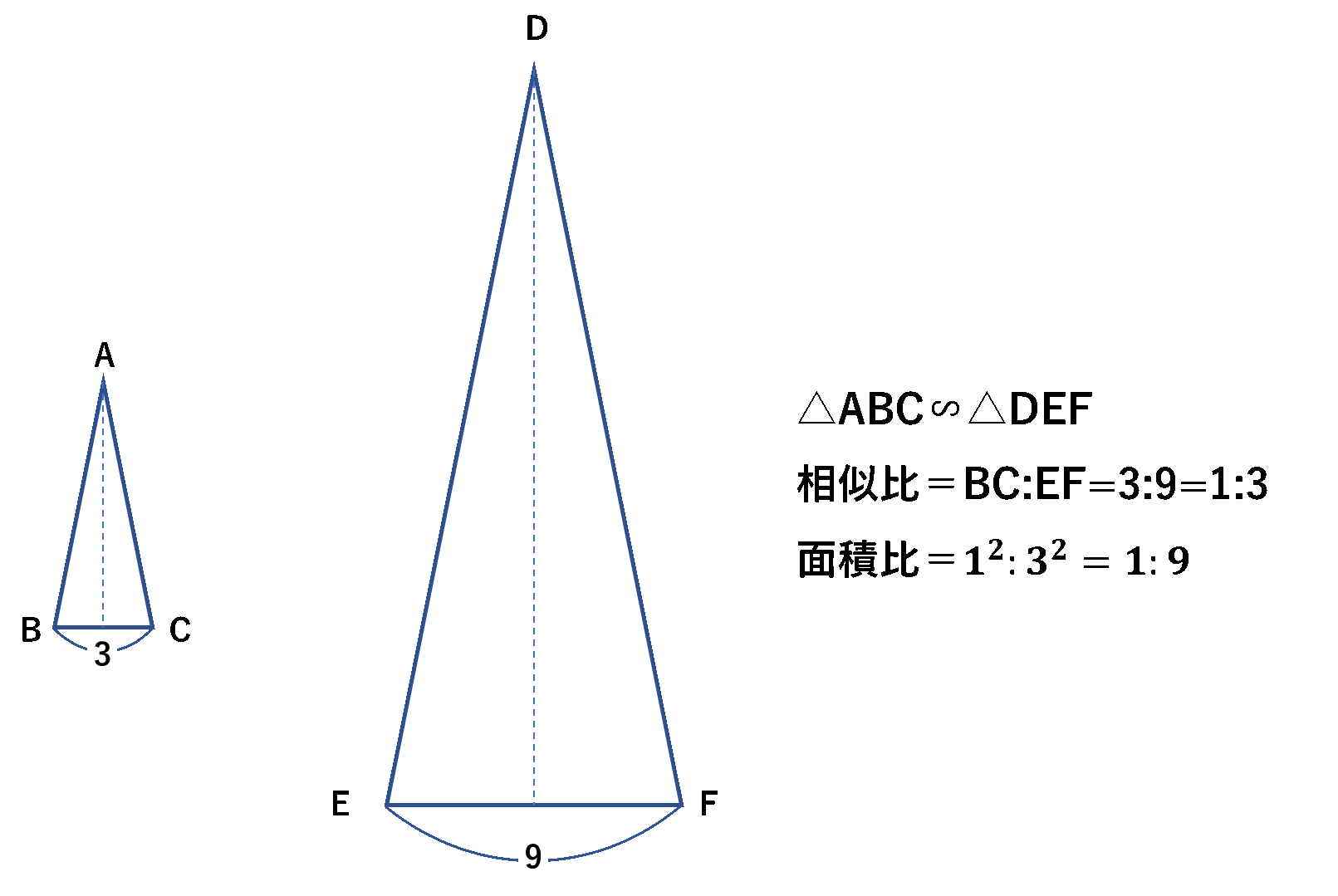
上図の例では、相似比は\(1:3\)となっています。二つの三角形を比べると、底辺の長さは\(3\)倍されており、高さも\(3\)倍になっています。三角形は合計で\(3×3=9\)倍されるため、面積比は\(1:9\)です。

この例を踏まえて一般的に相似な三角形の面積比は相似比の\(2\)乗になることが分かったと思います。加えて、実は三角形以外の図形に関しても相似な図形に関しては面積比が相似比の\(2\)乗になります。

まとめ

ここでは、相似と合同の違いや三角形の相似条件、相似比と面積比の関係について解説しました。相似な図形を見つけるには通常辺や角度などの条件を考慮する必要がありますが、円、正三角形や直角二等辺三角形は必ず相似な図形になります。例えば、正三角形は全ての辺の長さが等しいので辺の比が常に\(1:1:1\)で一定となり、直角二等辺三角形も\(2\)辺の比とその間の角が常に\(1:1\)と\(90°\)になります。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/須藤>