↓↓↓動画で見たい方はこちら↓↓↓

座標（平面）とは

座標（平面）とは、平面上の点の場所を座標とよばれる2つの数の組によって表せるような平面のことです。座標平面はよく\(xy\)平面ともよばれ、2つの数の組（座標）を\((x,y)\)などと表します。これは後で詳しく説明します。
座標平面のイメージなどが知りたい方はこちらの「座標の考え方」をご覧ください。
（参考：座標の考え方【算数からやさしく解説】）

座標平面に必要なもの

ここまででなぜ2つの数を使うのかについて説明してきましたが、次はどうやって点を2つの数で表すのかについて考えていきたいと思います。
まず、「座標の考え方」で考えたことから、平面に2つの数直線をそれぞれの原点で直行する（2本の直線が直角になる）ように置きます。
（数学ではよく下図のように数直線を配置し、左から右に行くにつれ大きくなる数直線を\(x\)軸、下から上に行くにつれ大きくなる数直線を\(y\)軸と言います。）

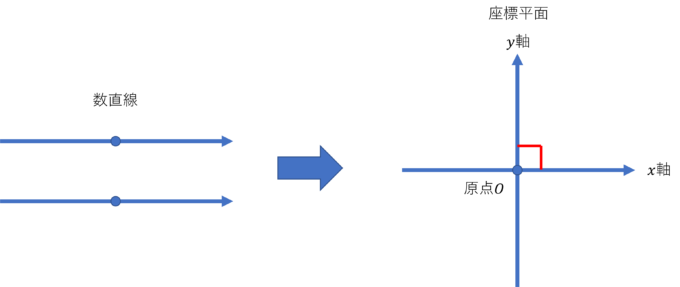
2つの原点が重なったところもまた（座標平面の）原点といい\(O\)(オー)で表します。
これで平面上の点を2つの数の組で表す準備はできました。

座標の表し方

それでは、実際にどのようにして点と座標を結びつけるのかを考えてみましょう。平面上の位置を知りたい点\(P\)から\(x\)軸、\(y\)軸のそれぞれに垂線を引きます。このときに交わった点を次のようにかっこの中に入れて
\begin{align}
(x軸と交わった点,y軸と交わった点)
\end{align}
のようにします。

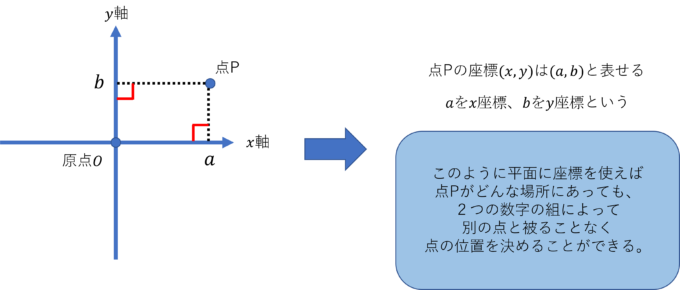
「\(x\)軸と交わった点」を\(x\)座標、「\(y\)軸と交わった点」を\(y\)座標と言いこれらの組を点\(P\)の座標と言います。
このように、ただの平面ではなく2つの数直線（\(x\)軸と\(y\)軸）が原点で直交していて、その平面上のすべての点を2つの数の組、座標\((x,y)\)で表せるような平面を座標平面と言います。

座標平面の活用例

今回の座標空間の説明で「直行する」2つの数直線を考えましたが、平面の場合2つの数の組さえできればある点の位置を表すことができるので、実は、特に直行していなくても平面上の2つの数直線が平行でなければたとえ斜めになっていても座標を考えることができます。
この斜めの数直線でできた座標を斜交座標と言います。また、原点からの距離と\(x\)軸からの角度を用いても平面上のすべての点を表すことができ、このような座標のとり方を極座標と言いい、平面の別の見方として、複素数について考えられるときなどに用いられます。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

座標の考え方【算数からやさしく解説】

<文/尾崎>