はじめに：同じ平均なのに、なぜ印象が違う？

「平均売上は去年と同じくらいなのに、なんだか今年は不安定な感じがする……」

ビジネスの現場では、こんなモヤモヤを感じることがよくあります。前回（第1回）では、四分位数や四分位範囲（IQR）を使って、データの“真ん中50％”の散らばりを見ました。

今回は、統計の世界で“ブレを測る代表選手”と言える、分散と標準偏差を取り上げます。

テーマはズバリ、

「式の暗記」ではなく、「平均からのズレの平均」というイメージをつかむこと。

数式そのものよりも、「ビジネスデータのどんな感覚を、どう数字にしているのか」をイメージで理解することをゴールに進めていきます。

---

1. 分散と標準偏差とは？一言で言うと「平均からどれくらいズレているか」

まず、分散と標準偏差をざっくり一言で表すと、こうなります。

分散・標準偏差 ＝ データが平均からどれくらいズレているかを表す指標

平均だけを見ていると、「全体として高いのか低いのか」はわかりますが、次のような情報はわかりません。

・月ごとの売上の上下が激しいのか、なだらかなのか
・メンバーごとの成果に、大きな差があるのか、みんな同じくらいなのか

こうした「ブレ」や「安定感」を数値で表すために使うのが、分散と標準偏差です。

---

2. 専門用語をかみ砕く：偏差・偏差の2乗・分散・標準偏差

分散や標準偏差を理解するために、まずは土台となる用語をやさしく整理しましょう。

偏差：各データ − 平均

偏差（へんさ）とは、

各データの値 − 全体の平均値

で計算される、「平均からどれだけズレているか」を表す数字です。

・平均より大きいデータ → 偏差はプラス（＋）
・平均より小さいデータ → 偏差はマイナス（−）

たとえば、平均残業時間が15時間の部署で、ある人の残業時間が20時間なら、

偏差 ＝ 20 − 15 ＝ ＋5時間

偏差の2乗：ズレをプラスだけで数える工夫

ところが、データ全体の偏差をそのまま足し合わせると、

・平均より大きいデータ（＋）
・平均より小さいデータ（−）

が打ち消し合ってしまい、合計が0に近づいてしまうという問題が起きます。

そこで、

偏差を2乗して、すべてをプラスにしてから平均をとる

という工夫をします。これが、分散のもとになっている考え方です。

分散：偏差の2乗の平均

偏差を2乗してから、その平均をとったものが分散です。

イメージとしては、

「平均からのズレの大きさ」を、2乗した世界で平均した値

と言えます。分散が大きいほど、データは平均から大きくズレている、つまりブレが大きいということになります。

標準偏差：分散の平方根（元の単位に戻した値）

ただし、分散には1つ欠点があります。それは、

「単位まで2乗されてしまう」ことです。

・データの単位が「時間」なら → 分散の単位は「時間²」
・データの単位が「万円」なら → 分散の単位は「万円²」

となり、感覚的にイメージしづらくなります。

そこで、分散の平方根（√）をとって、単位を元に戻したものが標準偏差です。

標準偏差 ＝ √（分散）

標準偏差は、分散と同じ情報を持ちながらも、単位が元のデータと同じなので、

「平均からのズレの大きさ」を、元の単位で直感的に理解しやすい指標

として広く使われています。

---

3. 売上データでイメージする「平均からのズレ」

ここからは、具体的な数値を使ってイメージを固めていきましょう。例として、あるチームの6か月間の月次売上（単位は万円）を考えます。

月	売上	平均売上	偏差（売上−平均）	偏差の2乗
1	100	100.0	0.0	0.0
2	110	100.0	10.0	100.0
3	90	100.0	-10.0	100.0
4	95	100.0	-5.0	25.0
5	105	100.0	5.0	25.0
6	100	100.0	0.0	0.0

この表を使って、次のステップを説明できます。

1. まず、6か月分の売上の平均値を計算する
2. 各月について「売上 − 平均」で偏差を出す
3. 偏差を2乗して、すべてプラスの値にする
4. 2乗した値の平均をとる → これが分散
5. 分散の平方根をとる → これが標準偏差

ここで大事なのは、

分散や標準偏差は、“平均からのズレの平均”を表している

というイメージです。式そのものは、「この考え方を数式で正確に書き下したもの」として捉えると、ぐっと理解しやすくなります。

---

4. 計算のとき「nで割る」のはなぜ？（3級ではここまで）

分散を計算するとき、

・分母を n で割る場合
・分母を n−1 で割る場合

がある、という話を見かけたことがあるかもしれません。

統計検定3級レベルでは、次のように考えておけば十分です。

3級では「nで割る」ほうをきちんと理解する。

より専門的な話（「標本分散」「不偏分散」といったテーマ）は、統計検定2級でしっかり扱われます。この回では、「nで割る形」がどんなイメージの指標なのかに集中しましょう。

分散 ＝ 「全部のデータの偏差²の合計を、データの個数 n で平均したもの」

と覚えておけば、ビジネスの実務では十分役に立ちます。

---

5. 標準偏差をグラフで見る：「多くの月はこのあたりにいる」

標準偏差は、グラフで見るとさらにイメージしやすくなります。

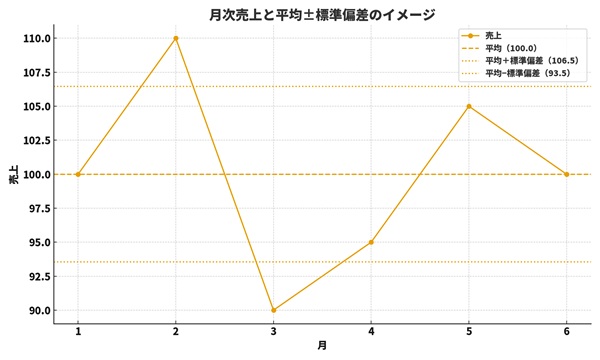
標準偏差が小さいとき：

・「平均 ± 標準偏差」の帯が細く、その中にほとんどの月の売上が入る
・グラフとしても、月ごとの売上が平均線の近くに集中している

標準偏差が大きいとき：

・「平均 ± 標準偏差」の帯が広くなる
・月によって平均から大きく離れた売上が多い

このように、

標準偏差は「データの多くが、平均のまわりのどれくらいの範囲に散らばっているか」をざっくり示してくれる

指標だと考えられます。

---

6. Excelで分散・標準偏差を出してみる

実務では、分散や標準偏差を手計算することはほとんどありません。多くの場合、Excel（やスプレッドシート）の関数を使います。

ここでは、代表的なExcel関数を、名前の意味も含めてかみ砕いて紹介します。

代表的な関数例

※Excelのバージョンによって関数名が異なる場合がありますが、考え方は同じです。

・分散を計算する関数（母集団全体とみなす場合）
　VAR.P(範囲) など
・標準偏差を計算する関数（母集団全体とみなす場合）
　STDEV.P(範囲) など

関数名の「.P」は、

Population（母集団）

の頭文字で、「全体」を対象としているイメージです。

実務の多くの場面では、

・チーム全員のデータ
・店舗すべてのデータ
・該当期間の売上すべて

といった「その場で扱っているデータ全体」を対象とすることが多いので、「P」のついた関数をイメージしておくとよいでしょう。

---

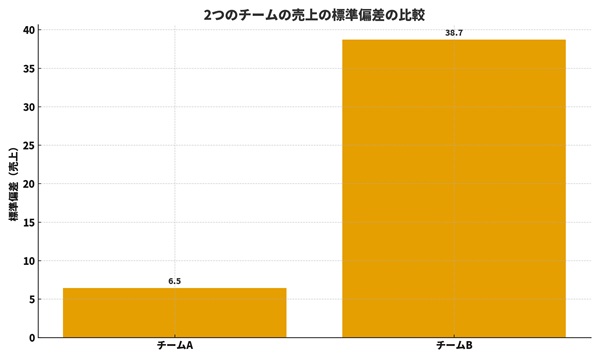
7. ビジネスの読み解き：標準偏差で「安定している／ブレている」を見分ける

最後に、分散・標準偏差をビジネスでどう読むかを整理します。

売上の標準偏差が大きいケース

・月によって売上が大きく上下している
・キャンペーン月と非キャンペーン月の差が極端
・一部の大口案件に数字が依存している

こうした場合、標準偏差は大きくなります。

「売上の標準偏差が大きい ＝ 売上が不安定・読みにくい」というサインです。

残業時間の標準偏差が小さいケース

・メンバー全員が、だいたい同じくらいの残業時間
・特定の人だけが突出して忙しい、という状況ではない

このような場合、標準偏差は小さくなります。

「残業時間の標準偏差が小さい ＝ 人による負担の差が小さい」と解釈できます。

平均値だけを並べているレポートに、標準偏差を1行足すだけでも、次のような問いが立てやすくなります。

・数字は伸びているが、安定しているのか？
・誰か1人だけに負担が集中していないか？
・安定しているチームのやり方を、他チームにも展開できないか？

---

8. まとめと次回予告

今回は、分散と標準偏差について、「式を丸暗記する」のではなく、

「平均からのズレの平均」をどう数字にしているか

というイメージを中心に解説しました。

ポイントのおさらい

・偏差 ＝ 各データ − 平均
・偏差の2乗 ＝ ズレをプラスだけで数える工夫
・分散 ＝ 偏差の2乗の平均（3級では「nで割る」形を理解すればOK）
・標準偏差 ＝ 分散の平方根（元の単位に戻した指標）
・標準偏差が大きい ＝ 平均からのズレが大きく、ブレが大きい
・標準偏差が小さい ＝ 平均の近くにデータが集まり、安定している

次回（第3回）は、今回の標準偏差を一歩進めて、

「変動係数」で売上や指標の“安定性”を比較する方法

を扱います。平均値が違う2つの会社・店舗・商品を比べるとき、標準偏差だけでは判断しにくい場面が出てきます。そこで登場するのが、

標準偏差 ÷ 平均 ＝ 変動係数（CV）

という考え方です。売上の「安定度合い」や、店舗ごとの「波の大きさ」を比較する際に、とても便利な指標なので、ぜひセットで身につけていきましょう。