ビジネスデータのブレ診断-第3回:変動係数で売上の“安定性”を比べる【統計学をやさしく解説】
公開日
2025年11月17日
更新日
2026年1月5日

この記事の主な内容
はじめに:「どっちの会社が本当に安定しているの?」
「A社のほうが売上規模は大きいけれど、B社のほうがブレが少ない気がする」
売上や来客数、アクセス数など、ビジネスの数字を比べるとき、こんな会話がよく出てきます。前回までの第1回・第2回では、
・四分位数・四分位範囲(IQR)で、データの散らばり具合を見る
・分散と標準偏差で、「平均からのズレの平均」を数値化する
というところまで進みました。
しかし、ここで1つ問題が出てきます。
「平均の大きさが違う2つのデータを、どうやって公平に比べるか?」
たとえば、売上規模がまったく違う2社を比べるとき、標準偏差の絶対値だけでは「どちらが安定しているのか」を判断しづらいことがあります。
そこで登場するのが今回の主役、変動係数(CV:Coefficient of Variation)です。
1. 変動係数とは?標準偏差 ÷ 平均で「ブレの割合」を見る
変動係数(CV)は、次の式で定義されます。
変動係数(CV) = 標準偏差 ÷ 平均
イメージとしては、
「平均に対して、どれくらいブレているか」の割合
を表す指標です。単位はなく、よく「〇〇%」というパーセント表示で使われます。
・CVが小さい → 平均に対してブレが小さい(安定している)
・CVが大きい → 平均に対してブレが大きい(不安定)
標準偏差は「絶対的なブレの大きさ」でしたが、変動係数はそれを平均で割ることで、
「相対的なブレの大きさ」= 安定性スコア
に変換している、と考えるとイメージしやすくなります。
2. なぜ変動係数が必要なのか?平均や標準偏差だけでは比べにくいケース
まずは、変動係数が必要になる典型的な場面を見てみましょう。
| 会社 | 平均売上(万円) | 標準偏差(万円) |
|---|---|---|
| A社 | 1000 | 100 |
| B社 | 300 | 70 |
この数字だけを見ると、
・A社の標準偏差:100万円
・B社の標準偏差:70万円
なので、
「絶対額で見るとA社のほうがブレている」
ように見えます。
しかし、平均の大きさまで考えるとどうでしょうか?
・A社は平均1,000万円の売上がある中での100万円のブレ
・B社は平均300万円の売上で70万円もブレている
「どちらが“相対的に”安定しているのか?」という問いには、標準偏差だけでは答えにくくなります。
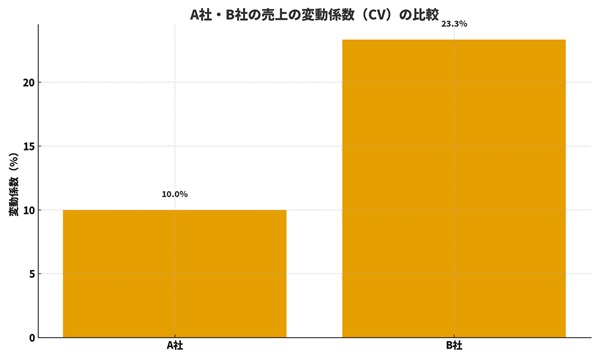
3. A社とB社を変動係数で比べてみる
ここで、先ほどのA社・B社に変動係数を適用してみましょう。
A社
・平均売上:1,000万円
・標準偏差:100万円
・変動係数:CV = 100 ÷ 1,000 = 0.10(10%)
B社
・平均売上:300万円
・標準偏差:70万円
・変動係数:CV = 70 ÷ 300 ≒ 0.23(23%)
こうして見ると、
A社:売上のブレは平均の10%程度
B社:売上のブレは平均の23%程度
という読み方ができます。
つまり、
B社のほうが、相対的に見るとブレが大きく、不安定である
と判断できるわけです。
| 会社 | 平均売上(万円) | 標準偏差(万円) | 変動係数(CV) | 変動係数(%) |
|---|---|---|---|---|
| A社 | 1000 | 100 | 0.10 | 10 |
| B社 | 300 | 70 | 0.23 | 23 |
4. 変動係数は「単位が違う」「平均が違う」データを比べるときに便利
変動係数の強みは、
単位や平均の大きさが違うデータ同士のブレを公平に比べられること
です。
単位が違うケースの例
・店舗A:1日あたり売上(円)
・店舗B:1日あたり来客数(人)
この2つは単位が違うので、標準偏差の絶対値を直接比べても意味がありません。しかし、
・店舗Aの「売上のCV」
・店舗Bの「来客数のCV」
という形にすれば、どちらが「その平均値に対してブレているか」を同じ“割合”として比べることができます。
平均が大きく違うケースの例
・店舗A:平均売上 200万円、標準偏差 30万円
・店舗B:平均売上 80万円、標準偏差 20万円
標準偏差だけ見ると、店舗Aのほうがブレが大きく見えますが、
・店舗A:CV = 30 ÷ 200 = 0.15(15%)
・店舗B:CV = 20 ÷ 80 = 0.25(25%)
となり、「平均に対するブレ」の割合で見ると、店舗Bのほうが不安定だとわかります。
5. 実務での使いどころ①:売上の安定性比較
まず、もっとも素直な使い方は、売上の安定性を比べる場面です。
・2社の売上を比べたい
・3つの店舗の売上の安定性を比べたい
・月別・四半期別の売上推移を「安定している期」と「不安定な期」に分けたい
といったときに、
「平均売上」「標準偏差」「変動係数」をセットで見る
ことで、次のような判断がしやすくなります。
・売上規模は小さいが、安定している店舗(CVが小さい)
・売上規模は大きいが、波が荒い店舗(CVが大きい)
| 店舗 | 平均売上(万円) | 標準偏差(万円) | 変動係数(CV) | 変動係数(%) |
|---|---|---|---|---|
| 店舗A | 200 | 30 | 0.15 | 15 |
| 店舗B | 120 | 40 | 0.33 | 33 |
| 店舗C | 180 | 20 | 0.11 | 11 |
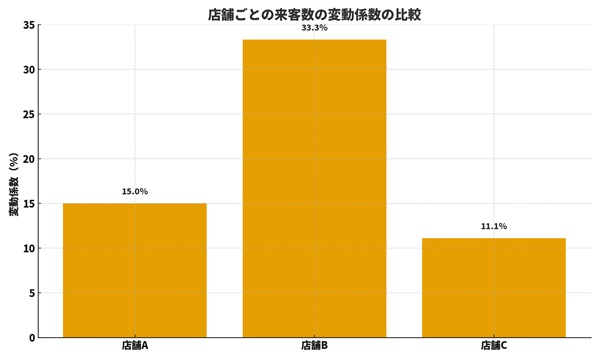
6. 実務での使いどころ②:店舗ごとの来客数の安定性
売上以外にも、来客数の分析にも変動係数は相性が良い指標です。
・店舗ごとの1日あたり来客数
・平日と休日で平均が違う場合の比較
・立地や業態の違う複数店舗の来客の安定性比較
たとえば、
・店舗A:平均来客数 200人/日、標準偏差 30人
・店舗B:平均来客数 120人/日、標準偏差 40人
だと、
・店舗A:CV = 30 ÷ 200 = 0.15(15%)
・店舗B:CV = 40 ÷ 120 ≒ 0.33(33%)
となり、「店舗Bは、日によって来客数のブレがかなり大きい」と判断できます。
7. 実務での使いどころ③:投資商品のリスク比較
変動係数は、金融・投資の世界でも、リスクの大きさを比べる指標としてよく登場します。
・投資信託A:平均リターンが高く、標準偏差も大きい
・投資信託B:平均リターンはそこそこだが、標準偏差は小さい
このとき、
「1単位あたりのリターンを得るのに、どれくらいのブレ(リスク)を受け入れているか?」
を比べるために、変動係数を使うことがあります。
ビジネスの意思決定でも、
・高い成長を狙うがブレも大きい戦略
・成長スピードは控えめだが安定している戦略
のように、「リターンと安定性のバランス」を評価する場面で、CVという考え方は応用できます。
8. 変動係数を使うときの注意点
変動係数はとても便利な指標ですが、使うときにはいくつか注意も必要です。
1)平均がほぼ0に近いときは、CVが極端な値になる
平均値がすごく小さいと、
CV = 標準偏差 ÷ 平均
の分母が小さくなるため、CVが異常に大きくなってしまうことがあります。そのようなケースでは、CVだけで判断するのは危険です。
2)分布の形までは教えてくれない
CVは「ブレの割合」の1つの指標にすぎません。
・左右どちらにブレているのか
・外れ値が多いのか
・特定の期間だけ極端に荒れているのか
といった情報までは教えてくれません。ですので、
グラフ(折れ線・箱ひげ図など)や、平均・標準偏差とセットで使う
ことが大切です。
3)同じ種類のデータ同士で比較する
CVは、単位が違うデータ同士も比べられるのが強みですが、解釈するときは、
・目的が近い指標同士(売上どうし、来客数どうしなど)
・期間や条件が似ているデータ同士
で比べたほうが、現場での腹落ち感は高くなります。
9. まとめ:変動係数を「安定性スコア」として使いこなす
今回は、変動係数(CV)を使って、売上や来客数などの“安定性”を比べる方法を整理しました。
ポイントのおさらい
・変動係数(CV)= 標準偏差 ÷ 平均
・「平均に対して、どれくらいブレているか」の割合を表す
・標準偏差だけでは比べにくい「平均が違う」データを、公平に比較できる
・A社とB社の例では、CVが10%と23%になり、B社のほうが相対的にブレが大きいとわかる
・売上、来客数、投資商品のリスクなど、「安定性」を評価したい場面で役立つ
・ただし、平均が極端に小さい場合や、分布の形を無視した使い方には注意が必要
変動係数は、ビジネスの現場で使いやすい、いわば
「安定性スコア」
のような指標です。平均・標準偏差とセットで確認するクセをつけるだけで、レポートの読み解きや意思決定の精度が一段上がります。
次のステップとしては、
・実際に自社や自部署の売上・来客数データにCVを計算してみる
・「平均が大きいけれど不安定な領域」「規模は小さいが安定している領域」を洗い出す
といった使い方を試してみると、変動係数が「使える指標」として定着していくはずです。














