はじめに：数字の山を整理する

会社で営業成績の一覧を見せられたとき、「数字がずらっと並んでいてよくわからない…」と思ったことはありませんか？ 例えば30人の営業担当者の1か月の売上額が、100万円の人もいれば200万円の人もいる。平均を出すだけでは、全体像が見えにくいものです。

こうしたときに役立つのが 度数分布表（どすうぶんぷひょう） と ヒストグラム です。生データを「整理して」「見える化」することで、数字の中に隠れたパターンを誰でも理解できる形にできます。

---

度数分布表とは：数字をグループにまとめる

例：営業1人あたりの売上額（30人分）

仮に30人の営業担当の月間売上額（万円単位）が次のようにバラバラにあるとします。

85, 90, 95, 100, 102, 110, 115, 118, 120, 122, 125, 128, 130, 132, 135, 138, 140, 142, 145, 150, 152, 155, 160, 165, 170, 175, 180, 190, 195, 200

このままでは「誰が一番か」「全体の傾向はどうか」がわかりにくいですよね。そこで、数字を範囲ごとに区切ります。この範囲を 階級（かいきゅう） と呼びます。

度数（どすう）とは

■ 各階級に「何人入ったか」を数えたもの。例えば100〜120万円に5人、120〜140万円に7人…という具合です。

相対度数（そうたいどすう）とは

■ 全体の中での割合。たとえば「100〜120万円が5人＝全体の16.7%」。

累積度数（るいせきどすう）とは

■ 下の階級から順に合計したもの。「140万円以下が何人いるか」といった見方ができます。

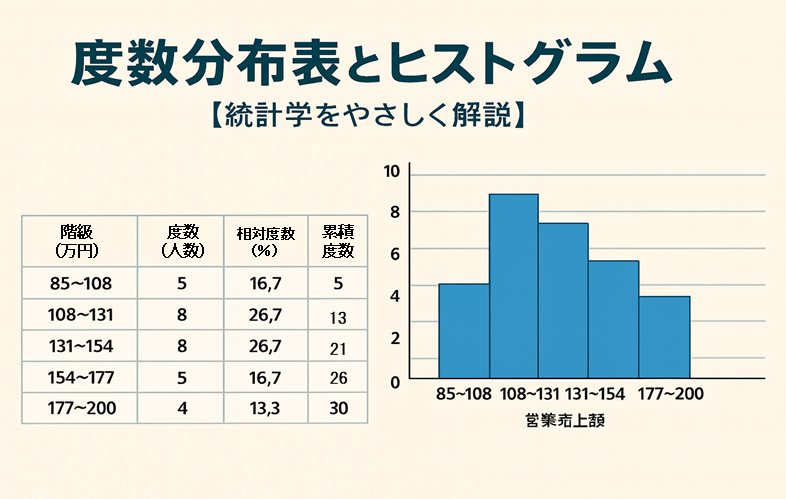
階級	度数（人数）	相対度数（%）	累積度数
85〜108	5	16.7	5
108〜131	8	26.7	13
131〜154	8	26.7	21
154〜177	5	16.7	26
177〜200	4	13.3	30

→ これで「どの金額帯に人が多いか」がはっきり見えてきます。

---

ヒストグラムとは：表をグラフにする

度数分布表をさらに直感的に見える形にしたのが ヒストグラム です。見た目は棒グラフに似ていますが、違いは「棒と棒の間が詰まっている」こと。これは金額が連続した値だからです。

実例：営業売上のヒストグラム

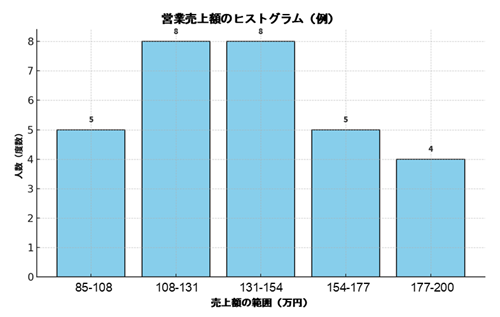
このグラフを見ると「120〜140万円に最も多くの営業がいる」「200万円近いトップ営業はごく少数」といった分布の特徴が一目でわかります。

専門用語をやさしく解説

■ 分布（ぶんぷ）：データが全体でどう散らばっているか。

■ 山の形：
・左右対称 → 平均的にばらけている
・右に裾を引く → 高額の人が少数いる（上位営業が目立つ）
・山が二つ → グループが分かれている可能性がある

棒グラフとの違い

■ 棒グラフは「カテゴリー別比較」（例：部署ごと）に使う。
■ ヒストグラムは「連続する数値の分布」（例：売上金額）に使う。

---

度数分布表とヒストグラムを使うと見えること

■ 平均ではわからない全体像：平均売上が130万円でも、実際には100万円前後が多いのか、200万円の人が引き上げているのかが分かる。

■ 戦略に役立つ気づき：「売上が120万円前後に集中している＝多くの営業が同じ壁にぶつかっている」「トップ層が少数だが突出している＝成功事例の共有が有効かも」。

■ 教育や研修の材料に：度数分布表を作ってグラフ化するだけで、チームの課題が浮かび上がります。

---

まとめ：数字を整理して“物語”を読む

度数分布表とヒストグラムは、「バラバラな数字」を「意味のある形」に変える道具です。
売上データ、顧客単価、アンケート結果など、ビジネスのあらゆる場面で活用できます。

次のステップでは「代表値（平均・中央値・最頻値）」を学ぶことで、分布の中心や典型的な値をさらに深く理解できるようになります。

数字をただ眺めるのではなく、そこから“物語”を読み解く力を、ぜひ身につけていきましょう。

<文/綱島佑介>