数学をする上でほとんどの人が（潜在的にでも）使っている古典論理は、強力で万能な論理です。この記事では、古典論理より非力で小さい論理である連言含意論理というものを話題にします。非力で小さいからといって、つまらないわけではありません。非力で小さい論理を糸口にたどっていった先には、けっこう壮大なメカニズムがあったりします。

古典論理

古典論理の「古典」は、「古くからあり標準的なもの」という意味です。「古い」とはいえ、「古くさくて今では使えない」という意味はまったくありません。古典論理は今でも現役バリバリであり、ほとんどすべての数学は古典論理の上に構築されています。（非古典論理がマイナーな存在。）

そんな古典論理で使われる論理記号は、次のようなものです。

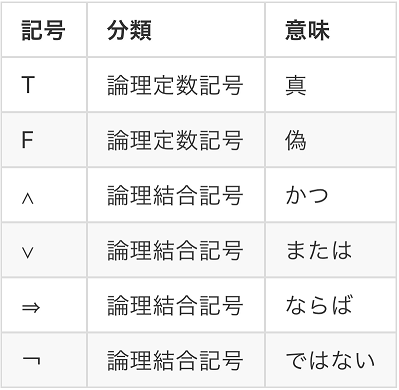
T は真（ほんと）である命題を表す記号ですが、「1 = 1 を短く書いた」と思ってかまいません。F は偽（うそ）である命題を表す記号ですが、同様に「1 ≠ 1 を短く書いた」と思いましょう。

論理結合記号（論理演算子記号とも呼ぶ）を使うと、単純な命題を組み合わせてより複雑な命題を作れます。例えば、(x > 0)∧(y > 0)⇒(xy > 0) は、丸括弧で囲んだ3つの単純な命題から、論理結合記号 ∧, ⇒ を使って組み立てたより複雑な命題です。(￢(x ≦ 0))⇒(x > 0) も丸括弧で囲んだ2つの単純な命題から、論理結合記号 ￢, ⇒ を使って組み立てています。単純な命題だと言った (x ≦ 0) も (x < 0)∨(x = 0) の略記とみなすことができます。

実用上は、限量子と呼ばれる記号 ∀ と ∃ も必要ですが、話が難しくなるので限量子は考えません。今回話題にする論理記号は、上の表に挙げた6つですべてです。6つの論理記号のセットは実は冗長で、機能性・能力を変えずに減らすことができます。

例えば、「ならば」を意味する記号 ⇒ は落とす（使うのをやめる）ことができます。A⇒B の代わりに (￢A)∨B を使えば、古典論理は何ら問題なく展開できます。ただし、「A⇒B の代わりに (￢A)∨B でも同じ」ことを納得するのはけっこう難しく、古典論理の難所のひとつです。

古典論理ではド・モルガンの法則と二重否定の法則という論理法則が成立するので、それを根拠に ∨ を落とす（使うのをやめる）ことができます。A∨B の代わりに ￢((￢A)∧(￢B)) を使えばいいのです。ですが、￢((￢A)∧(￢B)) はだいぶ面倒くさいですよね。論理記号を減らすと、かえって面倒で分かりにくくなるのです。よって、「減らせばいい」ってもんじゃないんです。6つを揃えておくのは、使い勝手からはベストだと思います。

さて、今名前を出したド・モルガンの法則ですが、それは次の形をしています。

・ ￢(A∨B) ≡ (￢A)∨(￢B)

ここで出てきた記号 ≡ は、古典論理の論理記号ではなくて、「左右にある2つの命題の論理的意味は同じ」であることを表す記号です。イコールを使ってもいいのですが、混乱の危険があります。例えば、「(x ≦ 0) と (x < 0)∨(x = 0) の論理的意味は同じ」であることを次のように書くと奇妙な気がするでしょ。

・ (x ≦ 0) = (x < 0)∨(x = 0)

(x = 0) のイコールは「数が等しい」意味で、それより左に出現するイコールは「命題の論理的意味は同じ」ことです。やっぱり区別したほうがいいですよね、次のように。

・ (x ≦ 0) ≡ (x < 0)∨(x = 0)

ちなみに（まー、余計な話なんですが）、≡ の代わりに ⇔ を使って次のように書けばいいじゃないか、と思った人もいるでしょう。

・ (x ≦ 0) ⇔ (x < 0)∨(x = 0)

実際上は、それでもいい（実害はほぼない）のですが、≡ と ⇔ は全然違うものです。≡ は命題（より正確に言えば論理式）について語るときに使うメタ記号です。一方 ⇔ は追加の論理記号で、∧ や ⇒ の仲間です。なに言ってるか分かんないですか？ ―― 分かんないですよね。僕〈檜山〉の過去のセミナー／将来のセミナーでは、ここらへんは重点的に解説しました／します。

連言含意論理

古典論理の6つの論理記号のうち幾つかを、古典論理の能力を保ったまま落とすことができます。その落とし方は一通りではありません。しかし、無闇やたらと論理記号を削り落とすと、古典論理が壊れてしまいます。極端な話、すべての論理記号を落としたら何もできなくなります。

古典論理は強力過ぎる（能力が高すぎる）のではないかと、昔から言われています。ほとんどの人はその強力さに全面的に依拠してますが、一部の人は古典論理を弱めて使うことに興味を持ちます。古典論理の6つの論理記号から、T, ∧, ⇒ だけを残し、他は使わないことにした論理を連言含意論理といいます。連言は ∧ のこと、含意は ⇒ のことです。

連言含意論理は、実際に古典論理よりずっと弱くなっています。否定の記号 ￢ がないので、ド・モルガンの法則 ￢(A∨B) ≡ (￢A)∨(￢B) は無意味です。二重否定の法則 ￢(￢A) ≡ A とか、排中律 A∨(￢A) ≡ T とかの有名な論理法則も、連言含意論理のなかでは解釈できません。

それでも、次のような論理法則は連言含意論理のなかでも解釈可能で、かつ成立します。

・ (A∧B)∧C ≡ A∧(B∧C)
・ T∧A ≡ A
・ A∧T ≡ A
・ A∧B ≡ B∧A
・ A∧B⇒C ≡ A⇒(B⇒C)

いずれも古典論理でも成立していた論理法則です。また、古典論理のなかで使用していた推論規則（すぐ後で説明）の一部は連言含意論理でもやはり使用できます。例えば、次のような推論規則です。

推論規則とは、真であることが既に分かっている命題から、真である命題を導き出す規則です。上の図のように、横線で上下を区切って表現します。上段の命題が真であるなら、下段の命題も真であることを表します。それぞれの推論規則の意味は以下のとおり。

1. A∧B が真であると既に分かっているならば、A は間違いなく真である。
2. A∧(A⇒B) が真であると既に分かっているならば、B は間違いなく真である。

こういう推論規則を幾つも積み重ねて、数学の証明が遂行されます。

論理記号、論理法則、推論規則を備えているという点では、連言含意論理も古典論理と同様な論理体系になっています。ただし、古典論理に比べると出来ることがはるかに少なくなっています。例えば、次は背理法に相当する推論規則ですが、連言含意論理では意味がありません（F も ￢ も入ってないので）。

連言含意論理の集合圏解釈

通常の数学における計算や証明を行っている人は、無意識に古典論理を使っています。それでも改めて古典論理を勉強すると難しく感じるのは、無意識にできてることを客観的に分析するのが難しいからです。多くの人は無意識に二足歩行してますが、改めて「どのようなメカニズムで二足歩行してるか？」と聞かれてちゃんと答えることは、解剖学やロボット工学の専門家でないと無理でしょう。難しい問いです。

しかしそれでも、ある程度のトレーニングをすれば、古典論理の論理計算や証明（推論の積み重ね）は出来るようになります。連言含意論理は古典論理の一部分（部分論理系）なので、連言含意論理の計算と証明も出来るようになるでしょう（がんばれば）。あなたは古典論理／連言含意論理の計算と証明に十分習熟したと仮定しましょう。

そんなあなたに悪魔（あるいは天使）がこうささやきます。「おまえがやっていた連言含意論理の計算は、命題の真偽に関する計算なんかじゃないかもね」と。もちろん、気持ちの上では「命題の真偽に関する計算」をしていたはずですが、気持ちはあなたの心のなかにあり、数学的実体ではありません。記号と数学的実体の対応関係は、気持ちではなくて明示的な定義で決まるものなのです。

親切な悪魔（あるいは天使）の忠告に耳を傾けてみましょう。連言含意論理において使ってきた記号には次のものがありました。

1. 命題を表す記号 A, B, C など
2. 典型的な真なる命題を表す記号 T
3. 連言（かつ）を表す記号 ∧
4. 含意（ならば）を表す記号 ⇒

これがあなたの気持ち（暗黙の心理的な想定）でした。ここで、気持ちを切り替えて、別な「記号から数学的実体の対応」を与えます。

1. 記号 A, B, C などは、集合を表す。
2. 記号 T は、単一の要素を持つ集合 {0} を表す。
3. 記号 ∧ は、2つの集合の直積を表す。
4. 記号 ⇒ は、2つの集合のあいだの関数からなる集合を表す。

つまり、

・ T := {0}
・ A∧B := A×B = {(a, b) | a∈A, b∈B}
・ A⇒B := [A→B] = {f | f:A→B という関数}

この解釈のもとで、論理法則 T∧A ≡ A は、{0}×A \(\cong\) A のことです。推論規則は、集合のあいだの関数〈写像〉になります。例えば：

これらの推論規則の解釈は以下のとおり。

1. 直積集合からの第一射影： \(\pi_1 : A\times B \to A, \:\: \pi_1(a, b) = a\)
2. 関数に入力を与えて出力を出す評価： \(ev : A\times [A \to B] \to B, \:\: ev(a, f) = f(a)\)

このように気持ちを切り替えても、すべての計算・証明は合理的な解釈が可能です。集合と関数〈写像〉達の世界を集合圏と呼ぶので、気持ちを切り替えた後の解釈は、連言含意論理の集合圏解釈です。

集合圏解釈に切り替えても、今までやってきた計算と証明の手順・やり方は一切変える必要がありません。気持ちをどう持っていようとも、行為は何も変わらないのです。

別な言い方をすると、もともとは古典論理の部分系だと思っていた連言含意論理の計算・証明は、手順・やり方は一切変えずに、集合圏における計算・証明としても通用するのです。これってオイシイと思いませんか？ 塀のペンキ塗りに習熟したら、同じ手首の動きで空手の技を既にマスターしていた、という感じです¹⁾。

ほんとにオイシイの？

連言含意論理の計算・証明は、集合圏での計算・証明と解釈することもできる、という話をしました。この話にはまだ続きがあって、連言含意論理を解釈する世界を集合圏に限る必要はありません。より一般に、デカルト閉圏と呼ばれるタイプの世界があれば、連言含意論理はそこでの計算・証明として解釈可能です。

そればかりではなく、計算科学／プログラム理論における型付きラムダ計算という計算体型も同じくデカルト閉圏における計算・証明として解釈可能です。ということは、連言含意論理、デカルト閉圏、型付きラムダ計算の三者は密接に関連していることになります。この三者の密接な関連性を、カリー／ハワード／ランベック対応といいます。

カリー／ハワード／ランベック対応には様々な変種があります。連言含意論理を構成した手順と同様にして、古典論理から F, ∧, ￢ の3つの論理記号を選んで古典論理より単純で弱い論理を作ります。単に古典論理より弱い部分系を作るだけでなくて、幾分か加工を加えます。できた論理をコンパクト論理と呼びます。コンパクト論理の計算・証明は、ベクトル空間と線形写像の圏における計算・証明として解釈可能です。より一般には、コンパクト閉圏と呼ばれるタイプの世界があれば、コンパクト論理はそこでの計算・証明として解釈可能です。

ベクトル空間と線形写像の計算といえば、行列・テンソルの計算です。結局、コンパクト論理、コンパクト閉圏、行列・テンソル計算の三者に密接な関連性があります。そう、これもカリー／ハワード／ランベック対応です。

なかなかにオイシイ話でしょ。

<文/檜山 正幸>

¹⁾オリジナルは映画『ベスト・キッド』〈The Moment of Truth / The Karate Kid〉(1984) 。2010年に、ジャッキー・チェン主演でリメイクされました。