∞『数秘の雅－江戸の算術に魅せられて』∞

時は流れても色褪せない算の美を求め、漢文に秘められた数学の宝石を掘り起こす冒険へのお誘いです。このセミナーでは、古き良き江戸時代の和算の粋を体験し、30の選りすぐり問題があなたの知性を刺激します！漢文で綴られた原典を手に取り、易解から深奥へと続く数学への旅路を歩みましょう。

伝統が息づく言葉たち、そして美しき方程式の表記法には、ただ計算する以上の物語があります。算木の一振りには、数百年前の知恵が宿り、それを解き明かすことで、あなたもまた、和算家の仲間入りを果たすのです。

さらに、選び抜かれた和算家たちの偉業に光を当て、彼らの業績を通じて数学の新たな地平を開きます。彼らの物語は、数学がただの数ではなく、文化と歴史を繋ぐ生きた証となる！！
このセミナーはただの講座ではありません。江戸時代から現代へと続く知の橋渡しであり、参加者一人ひとりが数学の深淵を覗き込む旅なのです。この機会に、和算の世界であなたの知性を磨き、数学の真の楽しみを見出してください。

■次の問題では、高さ3寸、底辺4寸の直角三角形内接する円の直径を求める問題で、答えが2寸であることを証明しています。

この問題の和算での計算方法は3+4-√(3^2+4^2)=2です。なぜ求まるかわかりますか？

和算書の数学では、問題（最初の2行）の後にすぐ（3行目）に答え「答えて曰く圓径は二寸」が記載されています。大事なことは、答えを求めることではなく、答えが導かれる道筋を楽しむことだと言っている気がします。また、底辺の長さを「殳」、円の直径を「圓」として、

方程式

を

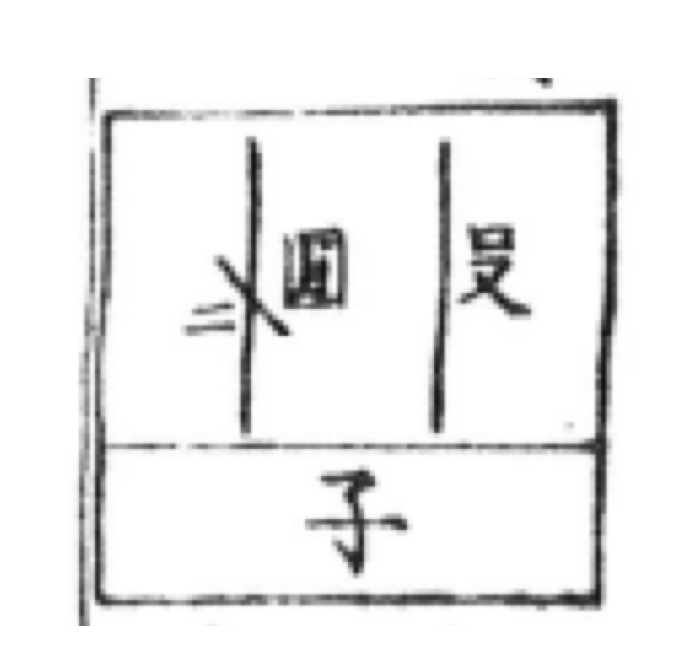
の様に、表記します。この独特の数学「和算」の世界をちょっと味わって見ませんか？