はじめに：平均だけ見ていると、現場でモヤモヤする理由

「平均売上は悪くないはずなのに、現場の体感は“ブレブレ”なんだよな…」

ビジネスの現場で、こんな感覚をもったことはないでしょうか？ 多くのレポートやダッシュボードでは、まず平均（平均値）が出てきます。しかし、平均だけでは、次のような疑問には答えてくれません。

・メンバーごとの数字に「バラつき」はないのか？
・月ごとの売上は、安定しているのか、ジェットコースターなのか？
・ごく一部の「超優秀」や「超異常」なデータに振り回されていないか？

この「バラつき」や「安定感」を数字でとらえるときに使うのが、散らばりの指標です。第1回のテーマは、その中でもとくに直感的で、ビジネスに応用しやすい四分位数と四分位範囲（IQR）です。

---

1. まずは「範囲」のおさらいから

統計検定4級レベルでは、散らばりの指標として範囲（レンジ）を学びます。

範囲 ＝ 最大値 − 最小値

もっとも大きい値と小さい値の差を見ることで、「どれくらい広く散らばっているか」をざっくり把握する指標です。

月	チームA売上	チームB売上
1	98	60
2	102	140
3	101	80
4	99	120
5	100	50
6	100	150

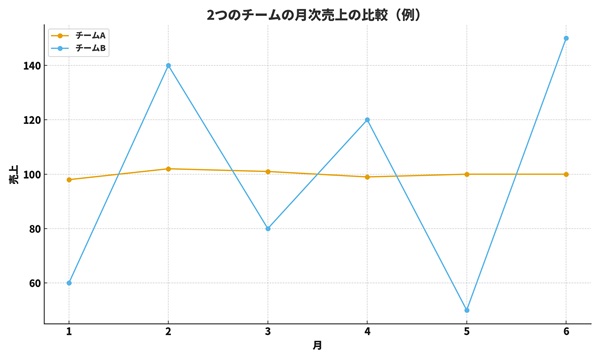
範囲はシンプルでわかりやすい一方、次の弱点があります。

・たった1つの極端な値に大きく左右される
　例：1人だけとんでもなく残業している人がいると、範囲が一気に大きくなる
・「ふつうの人たち」がどのあたりに集まっているかはわからない

そこで登場するのが、真ん中あたりのデータに注目する四分位数です。

---

2. 四分位数とは？「データを4つに割った位置」

データを小さい順に並べて、4等分する

四分位数は、データ全体を小さい順に並べて、4つに分けたときの区切りの値です。

・第1四分位数（Q1）：下から25％の位置の値
・第2四分位数（Q2）：下から50％、つまり中央値
・第3四分位数（Q3）：下から75％の位置の値

これらを使うと、次のような感覚を数字でつかむことができます。

・「下側のほうのデータはどこまでが“普通”なのか」
・「上側のほうのデータはどこから“やりすぎ”なのか」

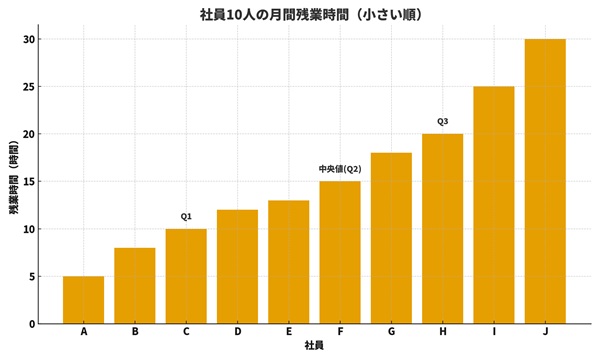
この表を使って、次のように説明できます。

・Q1 は「残業が少ないグループの上限」
・Q2（中央値）は「真ん中の人」
・Q3 は「残業が多いグループの下限」

「真ん中あたりの人たちが、どの範囲に集中しているか」を見ることで、データの散らばり具合をより現実的にイメージできます。

---

3. 四分位範囲（IQR）：真ん中50％の広さを見る指標

四分位数がわかったら、そこから一歩進んで四分位範囲（IQR：Interquartile Range）を使ってみましょう。

四分位範囲（IQR） ＝ 第3四分位数（Q3） − 第1四分位数（Q1）

IQRは、

「真ん中50％のデータがどれくらいの幅に収まっているか」
を表す指標です。

なぜ真ん中50％を見るのか？

ビジネスデータには、どうしても次のような「たまたま」の要素が含まれます。

・一時的なキャンペーンで急増した月
・システムトラブルで数字がガクッと落ちた月

これらの極端な値（外れ値）に振り回されず、ふだんの状態を把握したいときに、IQRが役立ちます。

・Q1〜Q3の幅が狭い → 多くのデータが似た値に集中している（安定している）
・Q1〜Q3の幅が広い → 真ん中の人たちの間でも差が大きい（ブレが大きい）

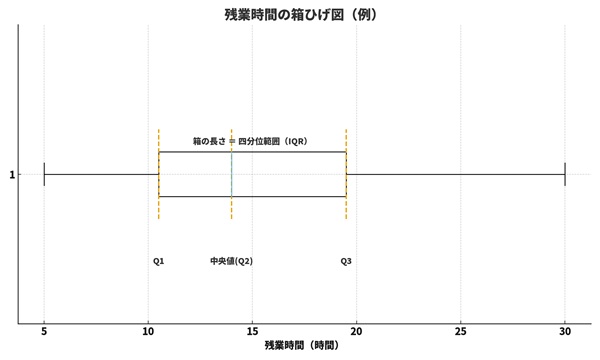
箱（Box）の部分だけを見れば、「真ん中50％がどのあたりに、どれくらいの幅で固まっているか」が一目でわかります。

---

4. 2つの部署を四分位数で比べてみる

ここで、残業時間の例をもう少しビジネス寄りに見てみましょう。たとえば、部署Aと部署Bの残業時間データがあるとします。

部署	平均残業時間（時間）	第1四分位数 Q1（時間）	中央値 Q2（時間）	第3四分位数 Q3（時間）	四分位範囲 IQR（時間）
部署A	15.6	11.0	14.0	19.0	8.0
部署B	15.6	5.0	12.5	28.0	23.0

このとき、こんな読み方ができます。

・平均はほぼ同じでも、
　部署A：IQRが小さい → 真ん中50％の人たちは似たような残業時間
　部署B：IQRが大きい → 真ん中50％の中でも、かなり差がある

・部署Bでは、同じ部署の中でも「残業が集中している人」と「ほとんど残業していない人」が混在している可能性

単に「どっちが長時間労働か」ではなく、

「残業が特定の人に偏っていないか？」

という組織マネジメント上の課題を見つけるヒントになります。

---

5. 四分位数・IQRは売上分析にも使える

残業時間の例だけでなく、売上データにも四分位数・IQRは応用できます。

・店舗ごとの1日の売上
・1顧客あたり購入金額
・1案件あたりの受注金額

などで、次のような問いに答えやすくなります。

・「大半の店舗は、どのくらいの売上レンジにいるのか？」
・「上位何店舗かだけが数字を引っ張っていないか？」
・「顧客単価がやたら高い一部の案件に、平均が引っ張られていないか？」

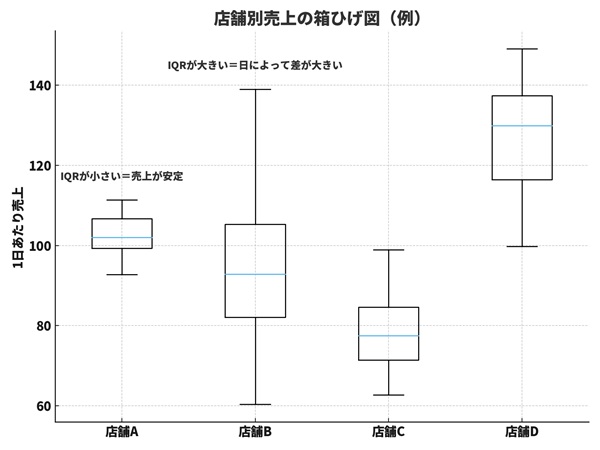
「平均売上」だけを見ていると、

・A店：平均売上は高いが、日によって大きくブレる
・B店：平均売上はそこそこだが、安定して売れている

といった違いに気づきにくくなります。四分位数・IQRを合わせて見ることで、

「売上規模」と「安定性」の両方を意識した評価
ができるようになります。

---

6. まとめと次回予告

第1回では、散らばりの指標の中でも直感的で実務に使いやすい、

・四分位数（Q1・Q2・Q3）
・四分位範囲（IQR）

を取り上げました。

ポイントを整理すると、次の通りです。

・散らばりを見るのは、「平均だけではわからない安定性や偏り」を知るため
・四分位数は、データを4等分したときの区切りとなる値
・四分位範囲（IQR）は、真ん中50％の広さを表す指標
・IQRが小さいほど、真ん中の人たちの数字が揃っていて「安定」
・残業時間・店舗売上・顧客単価など、ビジネスのさまざまな場面で活躍

次回（第2回）は、散らばりの指標としてさらに一歩進んだ、

分散と標準偏差で「平均からのズレ」を見える化する方法

を、数式に頼りすぎず、イメージ重視でやさしく解説していきます。分散・標準偏差は、統計学の世界で「ブレを測る代表選手」といえる存在です。ぜひ、今回の四分位数・IQRとあわせて、「ブレ診断の基本セット」として身につけていきましょう。