∞セミナーの概要と目標∞

20世紀の初頭に高木貞治・アルティンらによって構築された類体論は、多くの数学者によって最も美しい理論の一つと言われています。類体論は、アーベル拡大（ガロア群が可換になる拡大体）に関する理論ですが、類体論の完成直後から、ガロア群が非可換な場合に適用しようとする試みが続けられてきました。様々な試みがありましたが、1970年前後にロバート・ラングランズにより提唱された壮大なプログラム（ラングランズ・プログラム）が、非可換類体論の定式化の一つであると言われています。本セミナーでは、簡単な例を用いてラングランズ・プログラムの一端をご紹介する予定です。

1.フェルマーによる２平方定理（類体論のさきがけ）

フェルマーは、合同式\(x^2+1 \equiv 0 \pmod p\)(\(p\)は\(２\)以外の素数)が解をもつ条件を考え、これが\(p \equiv 1 \pmod 4\)であることを発見しました。

ここで、（やや唐突ですが）整数から\(\{0,\pm 1\}\)への関数\(\chi\)（ディリクレ指標と言われるもの）として

\[
\chi(n) = \begin{cases}
1 & ( n \equiv 1 \pmod 4) \\
0 & ( n \equiv 0 \pmod 2) \\
-1 & ( n \equiv 3 \pmod 4)
\end{cases}
\]
を考えましょう。すると、\(x^2+1 \equiv 0 \pmod p\)の解の個数は\(\chi(p)+1\)と表すことができます。\(\chi\)は、\(\chi(nm)=\chi(n)\chi(m)\), \(\chi(n+4)=\chi(n)\)を満たすなど、ある種の周期関数と考えられます。つまり、\(x^2+1 \equiv 0 \pmod p\)の解の個数が、ある種の周期関数（ディリクレ指標）によって表すことができました。多項式\(x^2+1\)はアーベル方程式（根を付加した拡大体のガロア群が可換群となるような方程式）です。そのため類体論が適用できました。この例は、類体論の最も簡単な場合と考えることができます。

2.非可換の場合の簡単な例

拡大体のガロア群が非可換となる典型的な多項式の例として、\(x^3-2\)を考えてみましょう。次の表は、100以下の素数\(p\)に関し、\(x^3-2 \equiv 0 \pmod p\)の解の個数を調べたものです。（なお、\(p=2,3\)のとき重解となりますが、その場合の解の個数は１としています。）

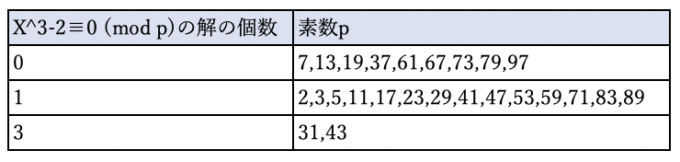
この表から、\(p\equiv 2 \pmod 3\)のとき解の個数は1つと予想できます（ただし、重解となる\(p=3\)は除いています。）。ところが、\(p\equiv 1 \pmod 3\)のときは、解が存在しない場合もあれば3つある場合もあります。このように解の個数を\(\mod 3\)で分類することはできません。別の自然数nを選んでも、解の個数を\(\mod n\)で分類することはできません。これは、ガロア群が非可換であることに由来します。

ところで、次の級数を考えてみましょう。
\[
q\prod_{n=1}^{\infty}(1-q^{6n})(1-q^{18n})
\]
この級数を展開すると次のようになります。

\[
q – q^7 – q^{13} – q^{19} + q^{25} + 2q^{31} – q^{37} + 2q^{43} \\- q^{61} – q^{67} – q^{73} – q^{79} + q^{91} – q^{97}+\cdots
\]

\(p\)を素数とするとき\(q^p\)の係数に注目してみましょう。\(p\equiv 2 \pmod 3\)のとき係数は0です。\(p\equiv 1 \pmod 3\)のとき係数は\(-1\)ですが、ただし、\(p=31,43\)のときは2となっています。これを上の表と比べると
「\(x^3-2\equiv 0 \pmod p\)の解の個数 \(= q^p\)の係数\(+1\)」
と表すことができそうです。

この級数はある種の周期関数（保型形式）と考えることができます。つまり、3次合同式の解の個数が、ある種の周期関数（保形形式）の係数で書けることがわかります。

3.ラングランズ・プログラムとは

ラングランズ・プログラムとは、上の例のように、方程式を\(\mod p\)したときの解の個数や因数分解の様子が、ある種の周期関数（ディリクレ指標や保型形式）と密接に関係していることを予想するものです。フェルマーの最終定理の解決の元となった志村・谷山予想も、楕円曲線を\(\mod p\)したときの点の個数が、保型形式（のフーリエ級数）で表されるというものであり、ラングランズ・プログラムの一つと考えることができます。

本セミナーでは、このような具体的な事例をみながらラングランズ・プログラムの一端を理解することを目標とします。

∞本編受講希望者の方向けの注意事項∞

・通信トラブル等が発生した時に、講師、受講生で円滑に連絡を取り合えるようLINEグループを作成します。LINEグループへの参加は必須とさせていただきますので、予めご了承ください。
・オンラインセミナー受講の際に必要となるパソコン、タブレットまたはスマホ等の通信機器、およびWiFi等のインターネット接続サービスは受講生ご自身でご準備いただきます。
・Apple Pencilなどのスタイラスペンやペンタブなど、画面にペンによる書き込み、描画を行える環境をご準備いただくことを推奨いたします。
・欠席者には録画動画だけでなく、セミナーで使用する配布資料(pdfファイルやurl等)も出席者同様配布いたします。

∞ロマ数トレランとは∞

「時間はかかってもいいから数学の美しさを中身からしっかり理解したい！」
聞いているだけでわくわくする華やかなテーマが満載のロマンティック数学ゼミ。
その根底となる理論からしっかり学びたい。ロマ数トレランはそんな声から生まれました。

ロマ数トレランは、ロマン溢れる数学を語ることができる講師による、講義形式ではなく、双方向の対話に重きをおいた受講者参加型の少人数制ゼミです。
実際に手を動かしたり、しっかりと質問、議論をする時間を設けることで
内容を確実に理解することを目標とします。同じ気持ちをもった仲間と一緒に学んだ先には新しい数学の世界が待っています。

～トレランとは～
山を縦走する山岳レースを意味するトレイルランニングの略です。
急坂は大変な時はありますが、いったん頂上に上がれば壮大な風景を楽しむことができます。
数学も同じです！平坦な道も、下り坂も、そして時にはハードな時もありますが、頑張って登りきれば素晴らしい風景が広がっているのです！

※ロマ数トレランでは受講生の理解に合わせて講師が適切な速度になるよう誘導しますが、受講者の理解を優先するため、カリキュラムの進度は確約いたしかねますので、予めご了承ください。
※質問の内容がセミナーの趣旨とそれる場合や、セミナーの適切な進行の妨げになると講師が判断した場合には、解説はセミナー内ではなく別途個別指導をご受講いただくようご案内することがあります。
※ロマ数トレランにはビデオ視聴以外に欠席保証はございません。ビデオは出席の有無に関わらずご視聴いただけます。