【ロマ数トレラン】ビジュアルリーマン予想入門
公開日
2014年5月4日
更新日
2025年7月8日

∞セミナー概要∞
本セミナーは、ゼータ関数の基本的な性質や、リーマン予想周辺の話題を、講師の木内先生による「ビジュアル リーマン予想入門」を使って丁寧に説明していきます。
メインテーマは素数とゼータ関数の関係です。ここではその概要をご紹介します。
1.素数
素数とは、1と自分自身しか約数を持たない自然数です。2,3,5,7,11,13,17,・・・ と続きます。素数でない1以外の自然数を合成数といいます。素数と合成数が、どのような順番で現れるのか簡単な規則がないことは皆さん経験的にご存じだと思います。
また、数が大きくなればなるほど素数が現れる確率は減っていきます。例えば、1から1000までの自然数には、素数は168個ありますが、1000000001(10億1)からの1000個の自然数の中には、素数は49個しかありません。
次の表は、それぞれの開始数から1000個の自然数のうち、素数の個数と割合を示したものです。このように、数が大きくなればなるほど素数の出現確率は低くなることが分かります。
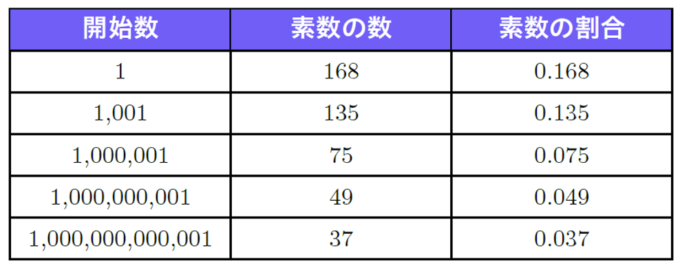
表1:自然数1000個あたりに含まれる素数の数と割合
この表では、開始数は、1000倍ずつ大きくなっていますが、素数の割合はそれほどには減っていません。この素数の出現割合はルジャンドルやガウスによって、1/log(x)で近似できると予想されました。この予想は、後にプーサンとアダマールによって証明され、素数定理と言われています。
次の図は、1,000,000,001~1,000,001,001の自然数のうち、素数の部分に黒線を引いたものです。

図:1,000,000,001~1,000,001,001の素数の位置
この図のとおり、素数は、一様に現れるのではなく、密度が高いところと低いところがあります。自然数における素数の分布状況を素数分布といいます。素数定理によって、素数の出現割合を近似的に予想することはできますが、実際に素数がどこに現れるれるのか、正確に知ることはできません。
2.ゼータ関数
リーマンは、報文「与えられた数より小さい素数の個数について」において、次のゼータ関数を導入しました。
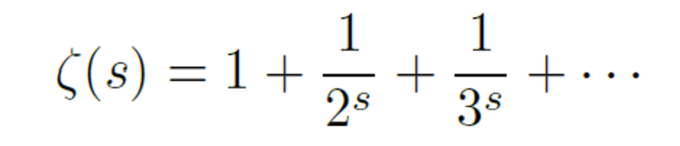
リーマンは、当時研究をしていた複素関数論を用いて、ゼータ関数がs=1を除く全複素平面上に定義域を拡張できることを示したうえで、負の偶数(s=-2,-4,-6,・・・)が零点(ζ(s)=0となるs)であることを示しました。この零点のことを自明な零点といいます。更に、リーマンは、自明な零点以外の零点(これを、非自明零点といいます。)が s=1/2+yi (yは実数)と書けると予想しました。この予想が後にリーマン予想と言われ、100万ドルの賞金がかかったミレニアム問題の1つとなりましたが、未だに最難関の未解決問題の一つと言われています。
リーマンは報文の題名を「与えられた数より小さい素数の個数について」と名付けていることからも分かるとおり、ゼータ関数を、当時はまだ証明されていなかった素数定理を証明するために導入したと言われています。リーマン自身は証明できませんでしたが、プーサンらによって素数定理はゼータ関数を用いて証明されました。
3.ゼータ関数と素数との関係
素数定理がゼータ関数を用いて証明されたこと分かるとおり、ゼータ関数と素数とは密接な関係があります。ここではその一つを見ていきましょう。
リーマン予想によると、ゼータ関数の非自明零点は、s=1/2+yi(yは実数)と書けます。y>0のうち、一番小さいものは、14.1(少数第2位以下は省略。以下同様)です。つまり、1/2+14.1iがゼータ関数の零点になっています。
この14.1を使って次のような関数を考えてみましょう。

このグラフは次のようになります。
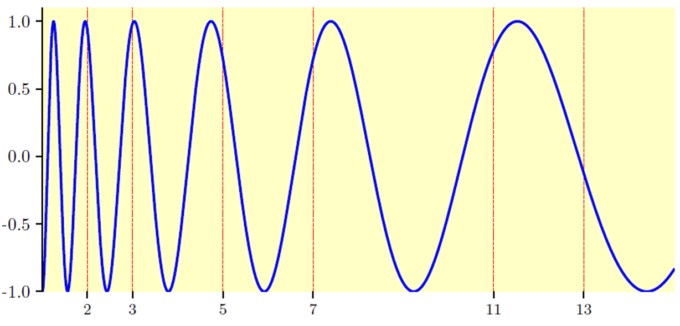
このグラフをみると、素数の近くで、極大値になっているように見えます。ただし、11と13には1つしか極大値がないなど、精度は高くなく、偶然かもしれません。
もうすこし、ゼータ関数の非自明零点について見ていきます。s=1/2+yiのうち、y>0のものを小さい順にならべると14.1, 21.0, 25.0, 30.4, 32.9, 37.6,・・・と続きます。そして、同様の関数を考え、これらの最初の10個の和をとります。
つまり、y =-cos (14.1 log x)- cos (21.0 log x)- cos (25.0 log x)-・・・を考えます。

このグラフをみると、グラフのピークと素数がぴったりと一致しています。ここまで一致すると偶然とはいえません。
このように、ゼータ関数の非自明零点のうち最初の10個から、素数でピークをとるグラフが作れましたが、逆に、素数からゼータ関数の非自明零点を表すグラフを作ることもできます。このように、素数とゼータ関数の零点は密接な関係があるのです。
本ゼミでは、素数やゼータ関数の基本的な性質を示したうえで、ゼータ関数の非自明零点と素数との関係をグラフを使って見ていきたいと思います。
受講対象
素数、リーマン予想に興味がある方
必要な数学知識
高校数学(複素数、指数、対数、三角関数、初等関数の微積分)
セミナー内容
第1回 素数の性質
・素因数分解の一意性
・素数が無限に存在すること
・素数定理
第2回 ゼータ関数の性質
・ゼータ関数の収束性
・オイラー積
・バーゼル問題
第3回 複素数と正則関数
・複素数とガウス平面
・ゼータ関数を複素数に定義域を拡張する
・正則関数の基本的な性質
第4回 ゼータ関数の定義域の拡張
・解析接続
・Γ函数の性質
・Γ函数の解析接続
第5回 ゼータ関数の解析接続と負の整数での値
・ Γ函数の零点と極
・ゼータ関数の解析接続
・ゼータ関数の特殊値
第6回 1+2+3+4+…=-1/12 ?
・オイラー・ラマヌジャンの不思議な方法
・総和法
・ゼータ関数の特殊値
第7回 ゼータ関数の関数等式
・オイラーによる関数等式
・リーマンによる関数等式
・関数等式の証明
第8回 リーマン予想
・関数等式の意味
・リーマン予想
・リーマン予想と同値な命題
第9回 ゼータ関数と素数の関係
・マンゴルトの明示公式
・素数定理のポイント
・リーマンスペクトル
第10回 素数で輝く
・素数と非自明零点との関係
・フーリエ変換と逆フーリエ変換
※質問内容やディスカッション内容により、上記内容は変更となることがあります。
セミナー基本構成
※内容によっては授業内に演習時間を含める場合がございます
∞本編受講希望者の方向けの注意事項∞
・通信トラブル等が発生した時に、講師、受講生で円滑に連絡を取り合えるようLINEグループを作成します。LINEグループへの参加は必須とさせていただきますので、予めご了承ください。
・オンラインセミナー受講の際に必要となるパソコン、タブレットまたはスマホ等の通信機器、およびWiFi等のインターネット接続サービスは受講生ご自身でご準備いただきます。
・Apple Pencilなどのスタイラスペンやペンタブなど、画面にペンによる書き込み、描画を行える環境をご準備いただくことを推奨いたします。
・欠席者には録画動画だけでなく、セミナーで使用する配布資料(pdfファイルやurl等)も出席者同様配布いたします。
※開催回ごとに多少構成が変わることがあります。
料金
定員
特定商取引法に基づく表示
セミナー監修
木内 敬 (きうち たかし)
<講師略歴>
京都大学理学部数学科卒業、京都大学大学院理学研究科数学専攻 博士課程 単位認定退学
弁護士を業とする傍ら、大人のための数学教室和からで数学講師を行う。専門は整数論。
やわらか数学ゼミ「素数の世界―世紀の難問『リーマン予想』とは」(2016年)の講師。
著書:「ビジュアル リーマン予想入門~グラフで解き明かす素数とゼータ関数の関係~」(技術評論社、2020年7月)
担当講師
※日程により一部講師が変わる事があります。
会場とスケジュール
本編(有料)
オンライン教室第01回 2024年6月8日(土) 14:00~16:30
第02回 2024年6月22日(土) 14:00~16:30
第03回 2024年7月6日(土) 14:00~16:30
第04回 2024年7月20日(土) 14:00~16:30
第05回 2024年8月3日(土) 14:00~16:30
第06回 2024年8月17日(土) 14:00~16:30
第07回 2024年8月31日(土) 14:00~16:30
第08回 2024年9月14日(土) 14:00~16:30
第09回 2024年9月28日(土) 14:00~16:30
第10回 2024年10月12日(土) 14:00~16:30
※最小履行人数は4名となります。最小履行人数に満たない場合、非開催となり、料金は返金させていただきます。開催有無は第一回ゼミの7日前に確定となります。
※ガイダンス回翌日18:00時点での申込数が定員を超えている場合は、抽選にて参加者を決定させていただきます。予めご了承ください。
※本編お申し込みの方にはご入金方法をメールでご連絡いたします。









